Description
A tense standoff brews between NewJeans and aespa. To decide who reigns as the best 4th-gen group, Minji and Winter are locked in a high-stakes Knight’s Tour duel.
Both idols command a knight starting from the top-left corner (0, 0), racing to visit every cell exactly once while following the fixed move order from the problem description.
Help Minji execute the perfect tour and outsmart Winter. If NewJeans wins, they’ll not only claim the 4th-gen crown, but fans might finally witness their long-awaited comeback (╥ᆺ╥;)

You are given a 0-indexed rectangular chessboard of size m × n.
A knight starts at the top-left cell (0, 0) and must move until every cell is visited exactly once.
At each move, you must record the step index into the current cell:
- The starting cell (0, 0) has value 0.
- After every legal move, the step index increases by 1.
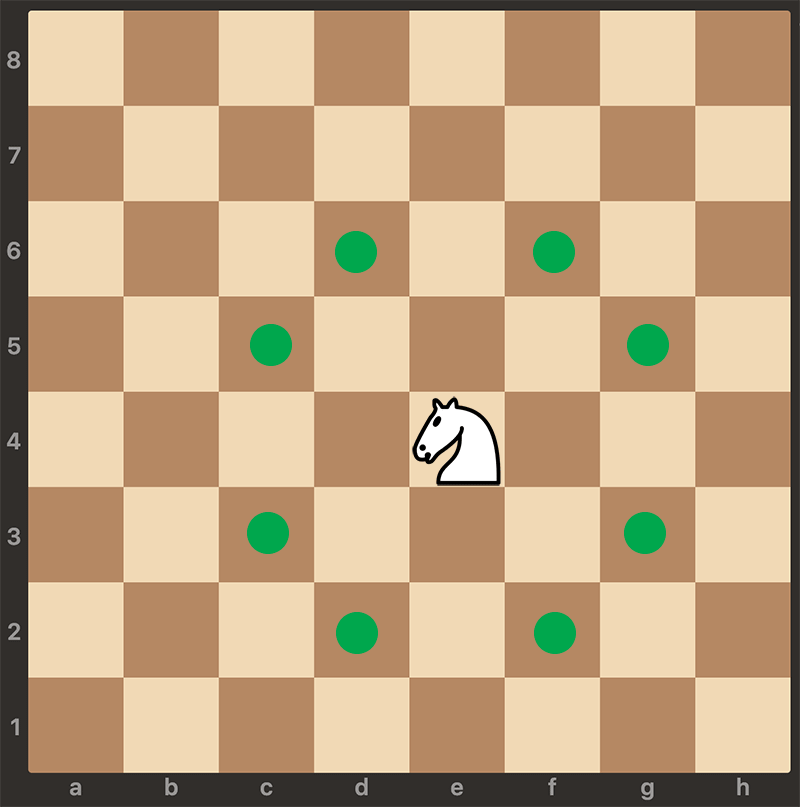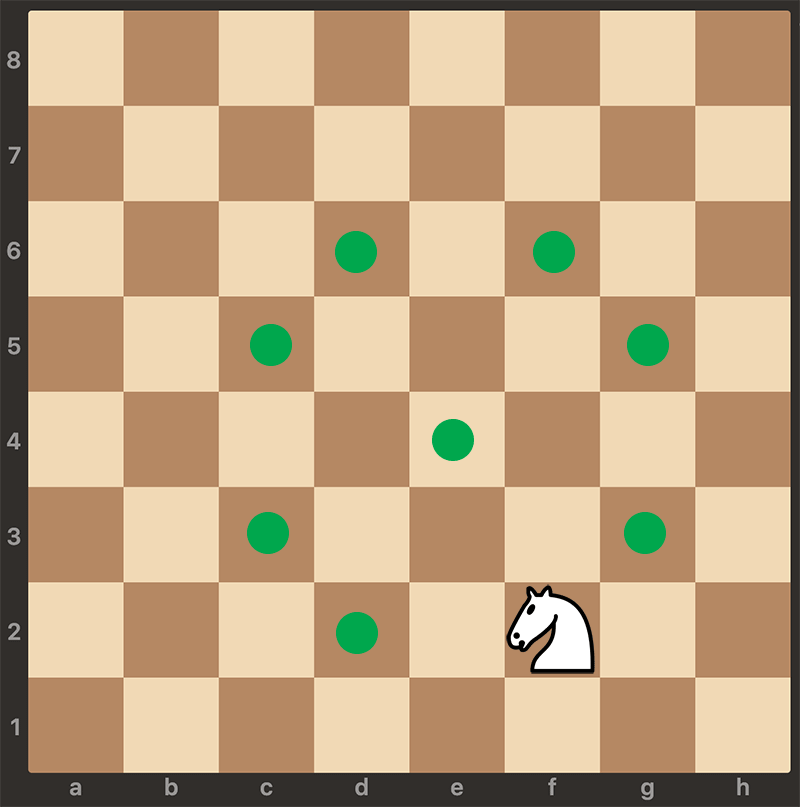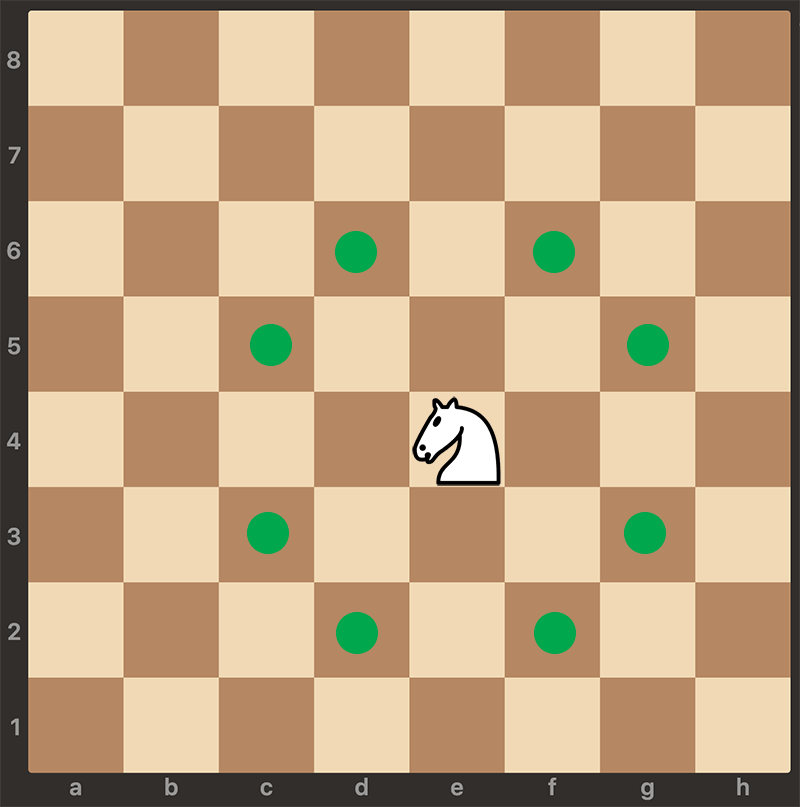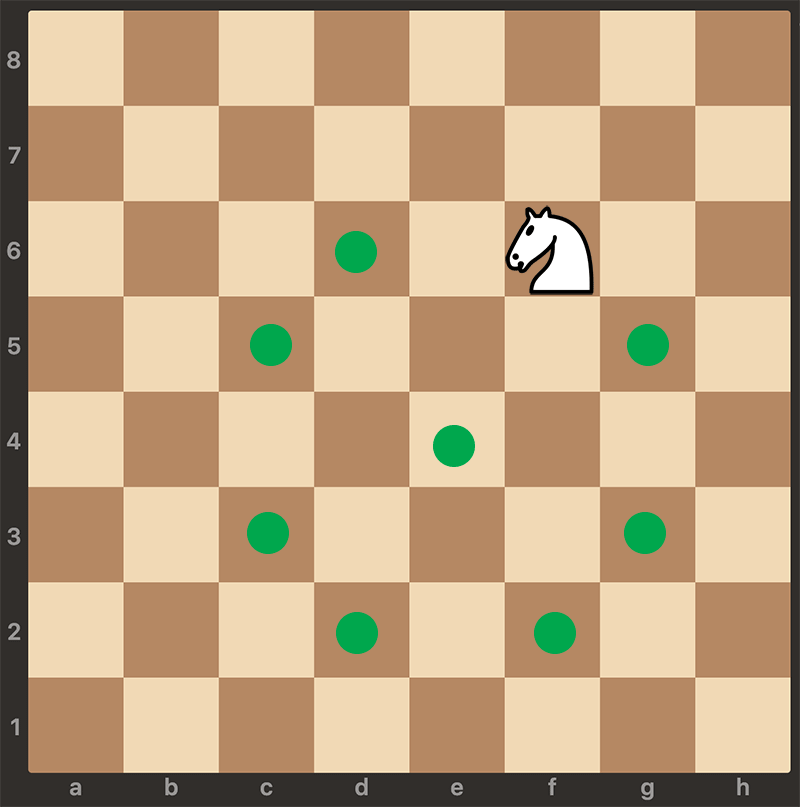
When choosing where the knight moves next, you must follow a fixed priority order of possible moves. At each step, try the following moves in order, and take the first valid one (i.e., inside the board and not yet visited):
- (i + 2, j + 1)
- (i + 2, j - 1)
- (i - 2, j + 1)
- (i - 2, j - 1)
- (i + 1, j + 2)
- (i + 1, j - 2)
- (i - 1, j + 2)
- (i - 1, j - 2)
Where:
- i represents the row index (0 ≤ i < m)
- j represents the column index (0 ≤ j < n)
Knight's moves reference:
Input
Two integers m and n, separated by a space — representing the number of rows and columns of the chessboard.
Constraints:
- 0 < m, n < 8
- It is guaranteed that for all given test cases, a valid knight’s tour exists.
Output
Print a 2D list representing the knight’s move order, where each element is the step index when the knight visited that cell.
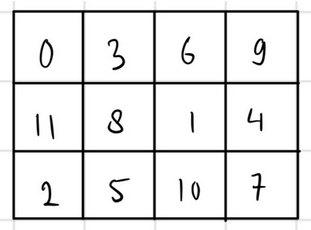
Example output (from # Sample out 1):
[[0, 3, 6, 9], [11, 8, 1, 4], [2, 5, 10, 7]]