Description
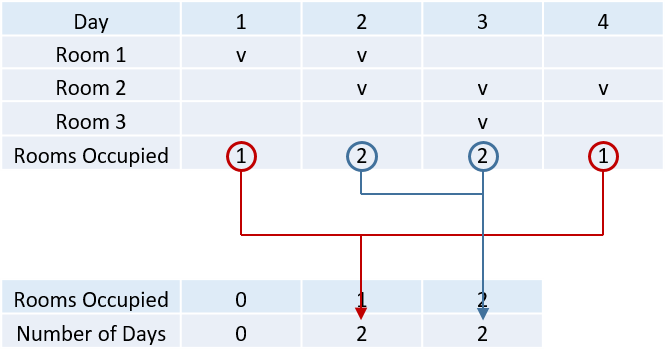
KuoTA's hotel has an infinite number of rooms. The manager wants to keep track of how many customers are there in his hotel. The $i$-th customer checks in at the $s_i$-th day and stay for $l_i$ consecutive days, in other words, the room will be occcuied on days $s_i$, $s_i+1$, ..., $s_i+l_i-1$. Since KuoTA is too busy launching his new business "八方來財", your task is to help him compute, for each possible occupancy level $k$ (where $k$ ranges from $1$ to $N$), calculate how many days exactly $k$ rooms are occupied simultaneously.
Input
The first line contain an integer $N$, the total number of customers.
Following are $N$ lines, each contain two integer $s_i$ and $l_i$, representing the day when i-th customer will check in and how long he will stay resepectively.
$N$
$s_1 \quad l_1$
$s_2 \quad l_2$
$\quad\vdots$
$s_N \quad l_N$
Constraints
- $1 \leq N \leq 2 \cdot 10^5$
- $1 \leq s_i, l_i, s_i+l_i-1 \leq 10^9$
Subtasks
- (Testcases 1~4): $N, s_i+l_i-1 \leq 3 \cdot 10^3$
- (Testcases 5~6): $s_i+l_i-1 \leq 2 \cdot 10^5$
- (Testcases 7~8): No additional constraint
Output
Output one single line containing $N$ integers, the $i$-th integer (1-based) is the total number of days that exactly $i$ rooms are occupied.