Description
CSSA's most handsome president Chang Cailou recently felt that riding motorcycles outdoors was too boring, so he developed a special Tetris game and would like you to help him test this game.
The special Tetris game screen has N rows and M columns. Every second, a block will fall until it reaches the bottom or rests on another stationary block.
When all cells in a row are filled with stationary blocks, that row will be eliminated, and all blocks above will move down one row.
The game lasts for T seconds, during which K blocks will be placed. Each block will be placed into the game at a designated time point P, in a 3×3 grid with top-left corner at coordinates (X, Y) . Any block's position and shape are guaranteed not to exceed the game boundaries and will only be placed in positions where no blocks have appeared before.
Finally, output the game screen at the time the game ends.
'*'represents blocks that will continue to move'#'represents stationary blocks that have stopped'.'represents position where no block has appeared yet
For sample input 2:
At time 2, 4, and 5, blocks will be added to the game screen.
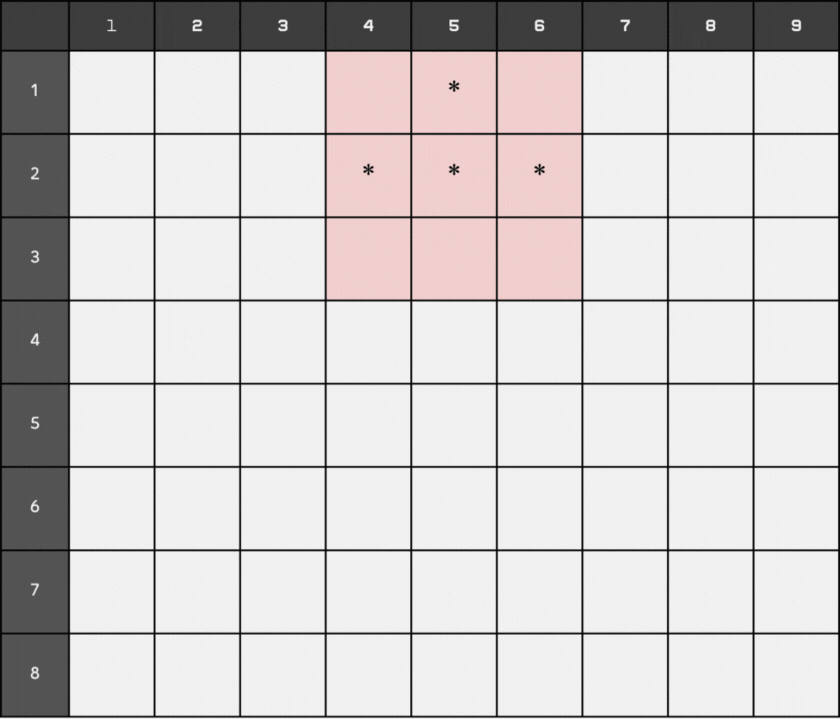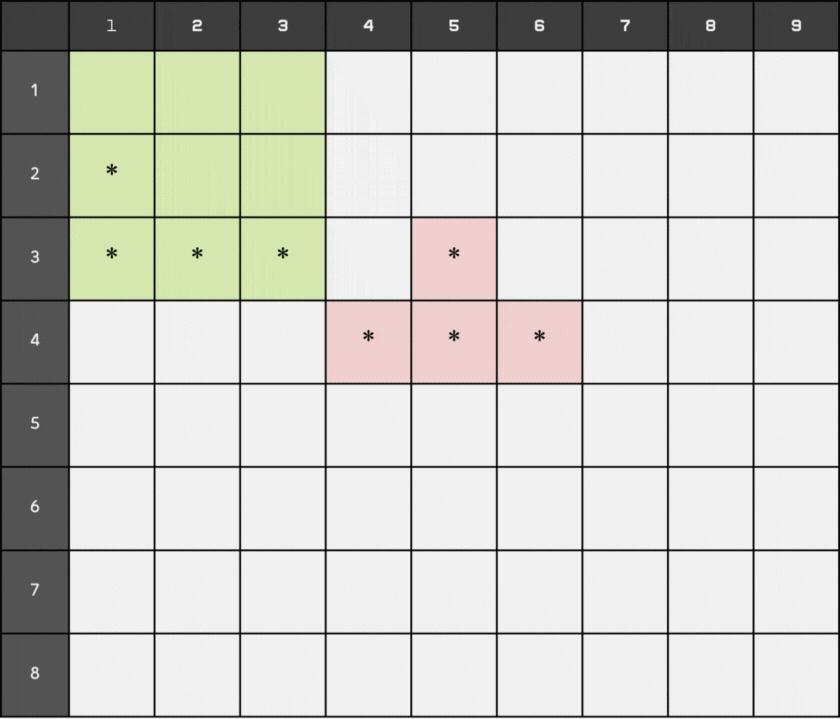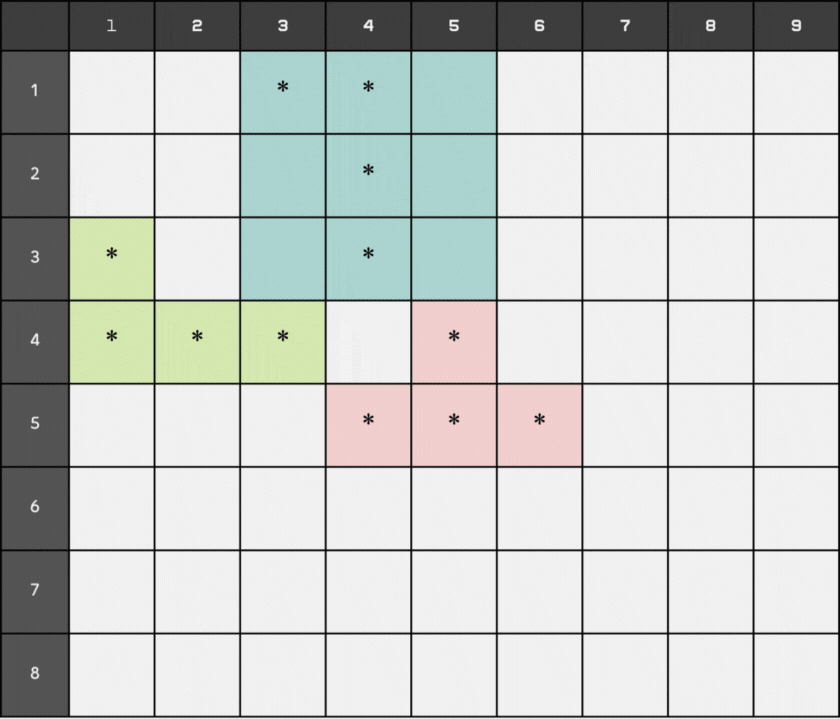
At time 8, a block is added at position (5, 7). At this moment, the first block that was added reaches the bottom and becomes stationary. It is represented by '#' instead of '*'.

When the time reaches 9, all blocks become stationary blocks. At this moment, the bottom row is entirely made up of stationary blocks, so an elimination is performed.


This problem is a partial judge.
Please implement functions defined in the header file.
- update: Update the game state to reflect the situation at P-th second.
- addBlock: Add a block to the scene at position (X, Y) .
- checkRow: Check whether the row needs to be eliminated.
- eliminate: Eliminate the row.
- print: Print the game screen.
Input
The first line contains three integers N, M, T, indicating the Tetris game size is N * M and the game lasts for T seconds.
The second line contains an integer K, indicating K blocks will be placed during the game.
The next K groups contain block information:
-
The first line of each group contains three integers Pi , Xi , Yi , indicating the i-th block will be placed at Pi seconds into the game, in a 3×3 grid with top-left corner at coordinates (Xi , Yi ) . Each placed block is guaranteed not to split.
Pi is guaranteed to appear in ascending order, and all blocks are guaranteed to have enough space for placement. -
Following this is a 3×3 grid using
'*'to represent cells with blocks and'.'to represent empty cells, showing the block's shape.
Constraints
- 1 ≤ N, M ≤ 100
- 1 ≤ T, P ≤ 15000
- 1 ≤ K ≤ T
- 1 ≤ X ≤ N
- 1 ≤ Y ≤ M
Subtasks
- Testcases 1 ~ 3: K = 1
- Testcases 4 ~ 6: No elimination operation
- Testcases 7 ~ 9: No additional restrictions
Output
Output the game screen at the time the game ends.
'*'represents blocks that will continue to move'#'represents stationary blocks that have stopped'.'represents position where no block has appeared yet
Please remember to print "\n" at the end.