Description
Registration Robots

Background
Thanks to advancements in AI and robotics, the organizers of the Taiwanese Lantern Festival are introducing a new robot model to help manage the large crowds this year.
This robot is designed to handle the registration process automatically and efficiently. With its wheels for smooth mobility and an advanced vision system (featuring two large, expressive eyes), it can navigate through the crowd and assist with registration based on the current queue situation. This ensures that everyone can enter the festival as quickly as possible, even during peak traffic.
Explanation
The government has provided significant funding to help the organizers deploy the new robot model. As a result, many registration robots are available this year, allowing multiple robots to handle family registrations simultaneously.
New families entering the festival must complete a registration process, which takes 2 minutes per family, like HW1. Once registered, they can proceed directly to join the festival activity.
Although there are many robots this year, their total number is still limited. Families must queue based on their arrival order and arrival time (like HW1), waiting for registration.
Similar to HW1, a certain number of families arrive each minute, each with a family ID and the price they have to pay.
Illustration of example:
At the start (0 minutes), all robots are lined up in a repair station, waiting in order based on their robot ID. The first in line is Robot 0 (R0), followed by Robot 1 (R1), then Robot 2 (R2), and so on.
- Robots move from left to right in a line, while families arrive and queue from right to left.
- If the frontest robot encounters an unserved family, it serves (does the registration task for) the family.
- And, the next robot becomes the frontest robot.
- When new families arrive, robots are dispatched from the repair station to assist them.

As robots leave the repair station, they move toward the family queue. Each robot encounters a family one by one and immediately begins the registration process (For example, the frontest robot will serve the first family). The remaining outside robots (if there are any robots outside of the repair station) continue moving rightward until they find a family to serve.
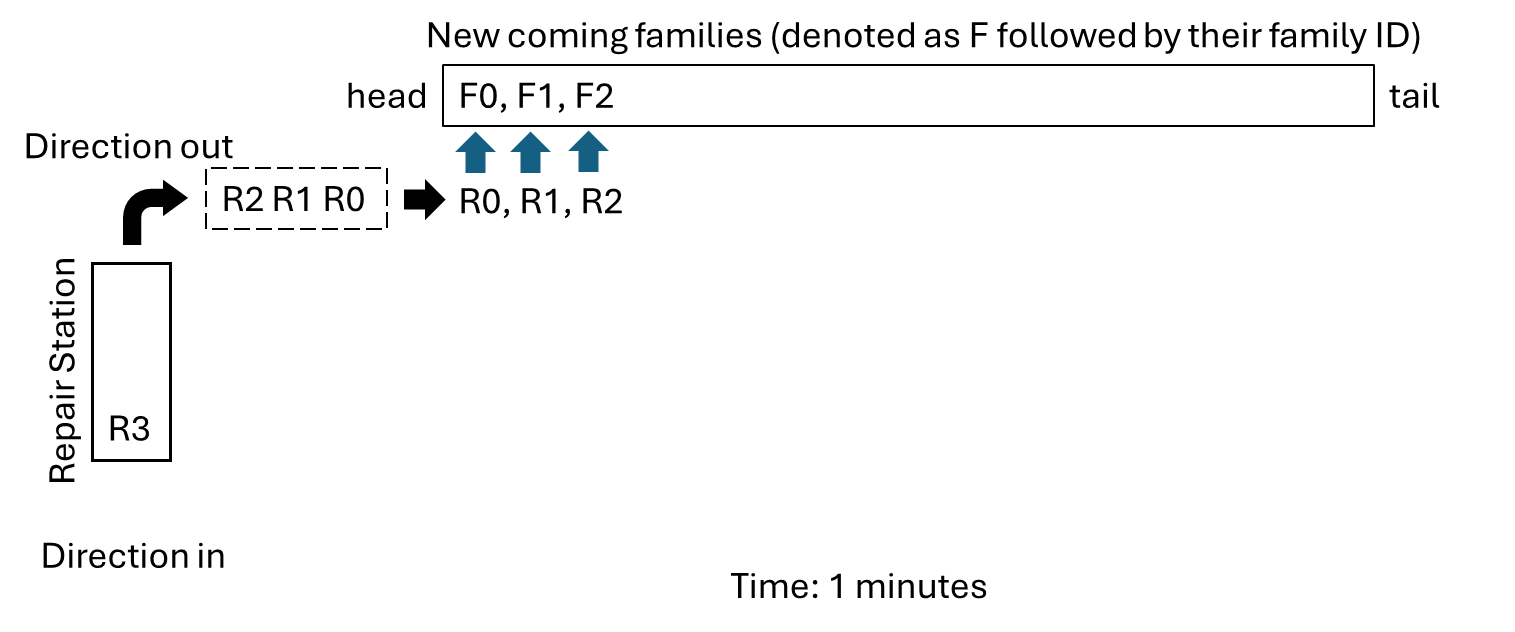
For example, if three families (F0, F1, and F2) arrive, the first three robots are dispatched:
They move rightward with R0 being the frontest robot. R0 encounters the first unserved family F0 (Family with ID 0) and processes the registration for F1. Then, R1 becomes the next frontest robot. R1 encounters the next unserved family F1 (Family with ID 1). And so on.
- R0 registers F0
- R1 registers F1
- R2 registers F2
Since only three families are in line, only three robots are dispatched, while the rest (R3) remain at the repair station
Note that we assume that the robots move instantly, so their moving time is ignored.
You don’t need to consider the moving time while solving the problem.
Once robots complete their registration, if no more families to serve, they become standby robots, waiting to find the next coming unserved family. If a/some standby outside robots already exist, then join them from the back (also maintain their relative position order).
- Robots maintain their relative position order while they finish the task and continue to search for the next family. Example: Once R0, R1, and R2 finish their task (their current position is R0 R1 R2 with R2 being the rightest among them) at minute 3 if there is no robot standby in front of them (there is no standby robot previously), R2 becomes the frontest standby robot, R1 becomes the next, and R0 becomes the last.
- If there are already enough available (standby) robots outside, no new robots will be dispatched from the repair station.
- If all the outside robots are processing and there is still any unsaved family in the queue, then dispatch the remaining robots (if there are any) from the repair station according to the number of current unserved families in the queue.
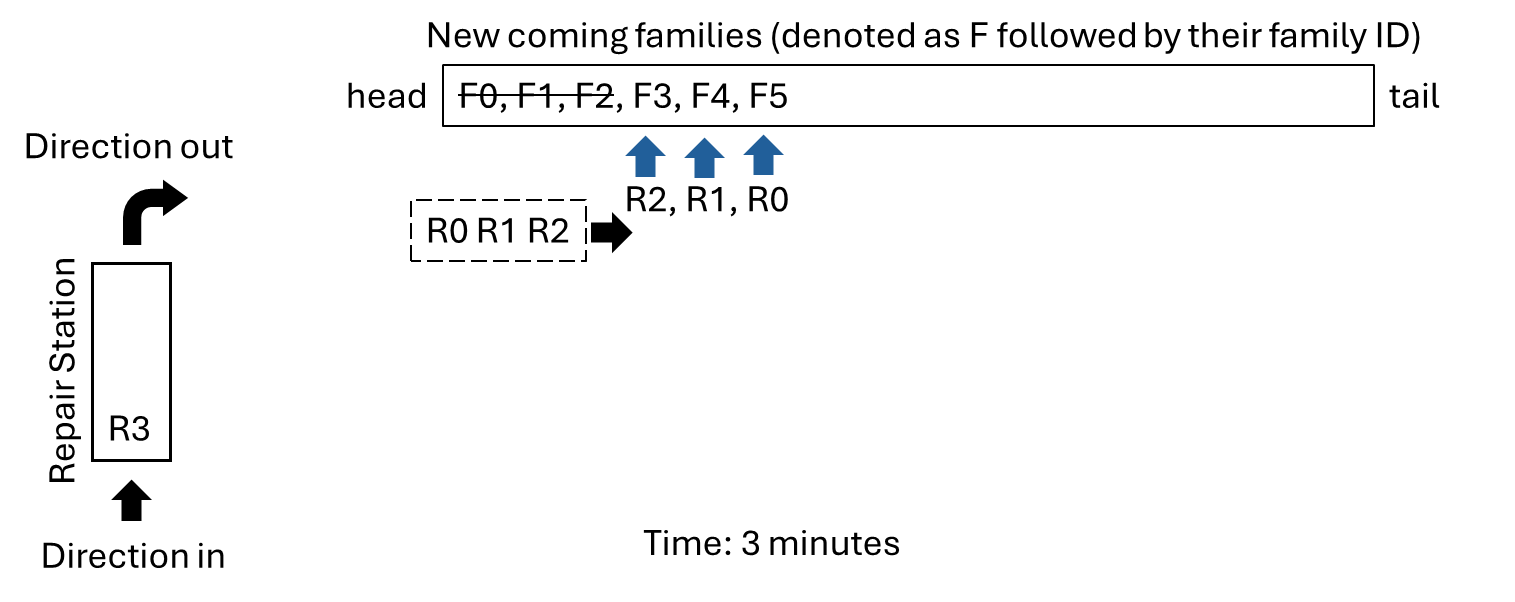
By minute 3, R0, R1, and R2 have finished their 2-minute tasks. At the same time, three new families (F3, F4, F5) arrive.
Instead of dispatching new robots, the outside available robots continue moving rightward to find any unserved families: As mentioned, the frontest robot (R2) encounters the first unserved family(F3). And so on.
- R2 serves F3
- R1 serves F4
- R0 serves F5
By the next time (4 minutes), new families arrived, since we didn’t have any available robots on standby outside, we dispatched the R3 to serve the F6.
However, we don’t have more robots so F7 will keep waiting in the queue.

The green arrow means they have processed for 1 minute. The blue arrow means they just start the process.
At the next time step (5 minutes), R2, R1, and R0 have just finished their tasks. As we have mentioned, they automatically move rightward, passing by all the working robots, and becoming on standby to find the next family that needs registration.
R0 meets F7 to serve. R1 and R2 are on standby, waiting to find a new family. Note that, R1 is in front of the R2.

At the next time step (6 minutes), R3 will have just finished its task, and new families F8, F9, and F10 will arrive.
- R1 which is on standby, will encounter the first unserved family, F8, and begin the registration process.
- R2 will then meet F9 and start serving them.
- R3 who has just finished its previous task, will continue moving forward until it reaches F10 and begins its registration.
Those robots are on standby have priority over the just-finish robot.

Battery Check
Since the robots operate on electrical power, strict battery management rules must be followed. After completing Y registration tasks, a robot must return to the repair station for a battery check.
Battery checking takes 1 minute. It means that if this minute a robot goes for a battery check. Then, in the next minute, it will be in the repair station and available to serve.
For example, if Y = 10, it means that if a robot has processed registrations for 10 families, it must go back to the repair station to check its battery status immediately.
After the check, it can be dispatched again at the next minute if necessary.
If multiple robots need to go back for a battery check at the same time, they will enter the repair station in the same order. For example, R3 is the frontest, R2 is the next, and R1 is the last. This ensures a smooth moving process.
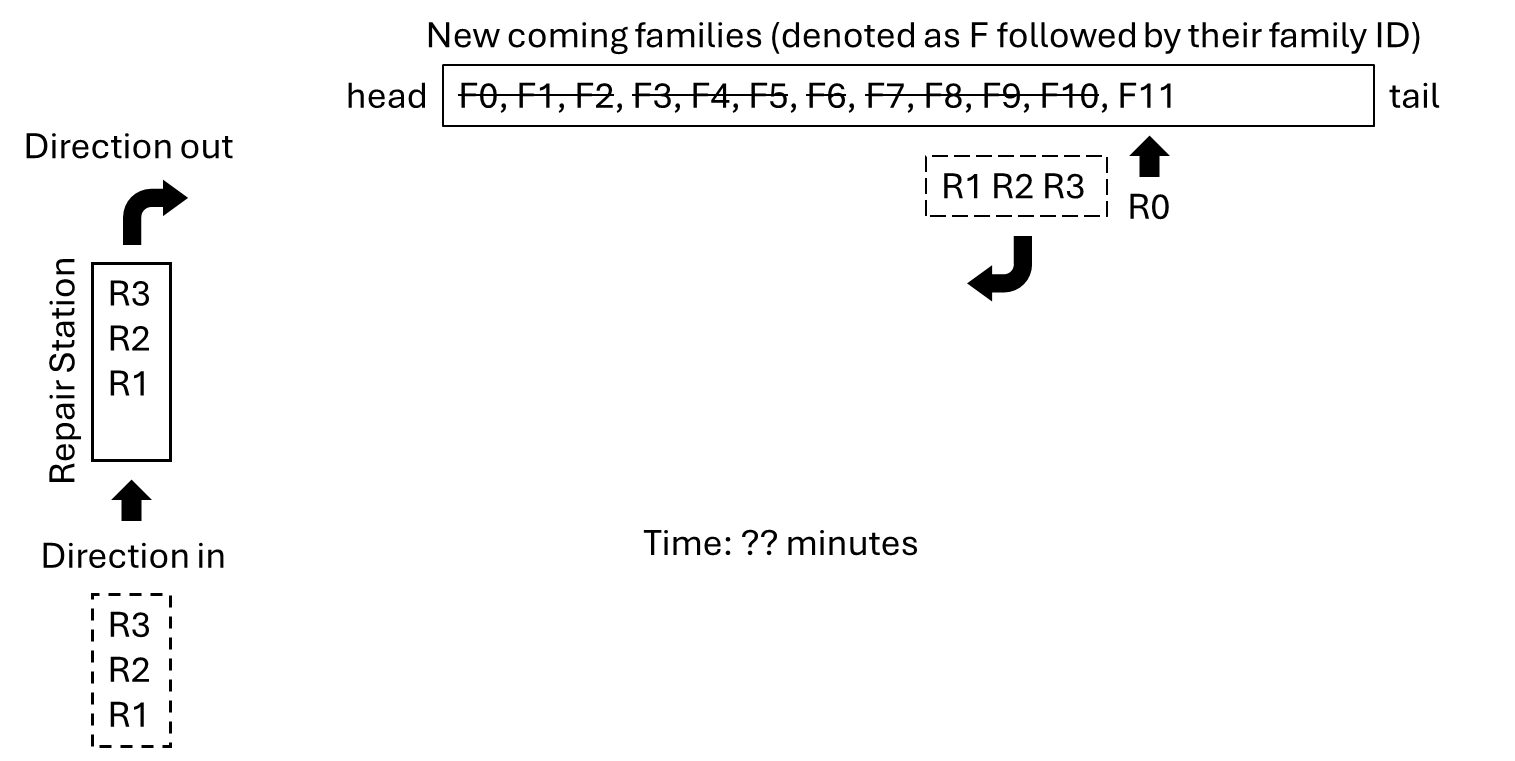
Quick Summary
- Multiple robots manage the festival's registration process.
- Once dispatched, a robot stays outside until it reaches its registration limit.
- Each registration takes 2 minutes.
- Families pay the robot that registers them after registration has been completed.
- Families queue based on their arrival time and order.
- Once robots complete their tasks (unless they need a battery check), if there is no more family, they become standby outside robots, maintaining their relative positions. If other robots are already on standby outside, they should join the group at the end of the line.
- Robots follow a specific movement rule, and relative positioning determines which robot serves which family.
- Take care of the battery check if a robot runs out of its registration limit.
Test case difficulty level:
1. Only a few robots and a few families will come, no battery check event.
2. Robots are more than coming family. No battery check event.
3. Several Robots and families which the number of families is several times the number of robots. No battery check.
4. Frequent battery check (Y is small).
5. Cover all conditions.
Input
The first line of input will be 3 numbers, N, Y, M
- N is the number of robots we have this year (their ID are 0, 1, 2, …, N-1)
- Y is the number of registration limit (each robot after processing Y registrations needs to go back to the repair station for battery-checking)
- M is the minutes to simulate (from 1 to M)
The following M lines indicate the new families that arrived at the i-th minutes (i from 1 to M)
Each line means the list of pairs of their family ID, and the price they need to pay separated by a comma, and each pair is separated by a space.
For example:
0,100 1,100 2,100 3,400 4,200
5,100 6,200
7,220
The family ID is determined by their arrival order. The first coming family has its ID 0.
Output
List the robot's information from Robot 0 to Robot N-1
- Robot ID
- Number of families the robot has completed their registration (only consider the families that have finished their registration)
- The total price they have collected
- Number of times that the robot had their battery-checking
List the family’s information (only for the families who have finished their registration)
- the family ID
- The ID of the robot that processes them
- the moment (which minutes) that they finish their registration
Don’t forget to add a new line at the end