Description
Big Orange Cat (大橘) found a strange orange tree in his backyard, represented as a syntax tree with n nodes. Each node is either a number or an operator, including basic operators (+, -, *) and m custom operators.
Each custom operator (the i-th one) is defined as follows:
- oi: the symbol representing the operator.
- ki: the number of input parameters (child nodes) it accepts.
- si: the preorder traversal of the syntax tree defining its computation rule, consisting of +, -, *, numbers, and operators defined earlier. In other words, the syntax tree of a custom operator may include other previously defined operators; please refer to Example 6.
In the syntax tree, parameters are denoted as A (first parameter), B (second parameter), and so forth. For example:
Explanation of Sample Test Case 6:
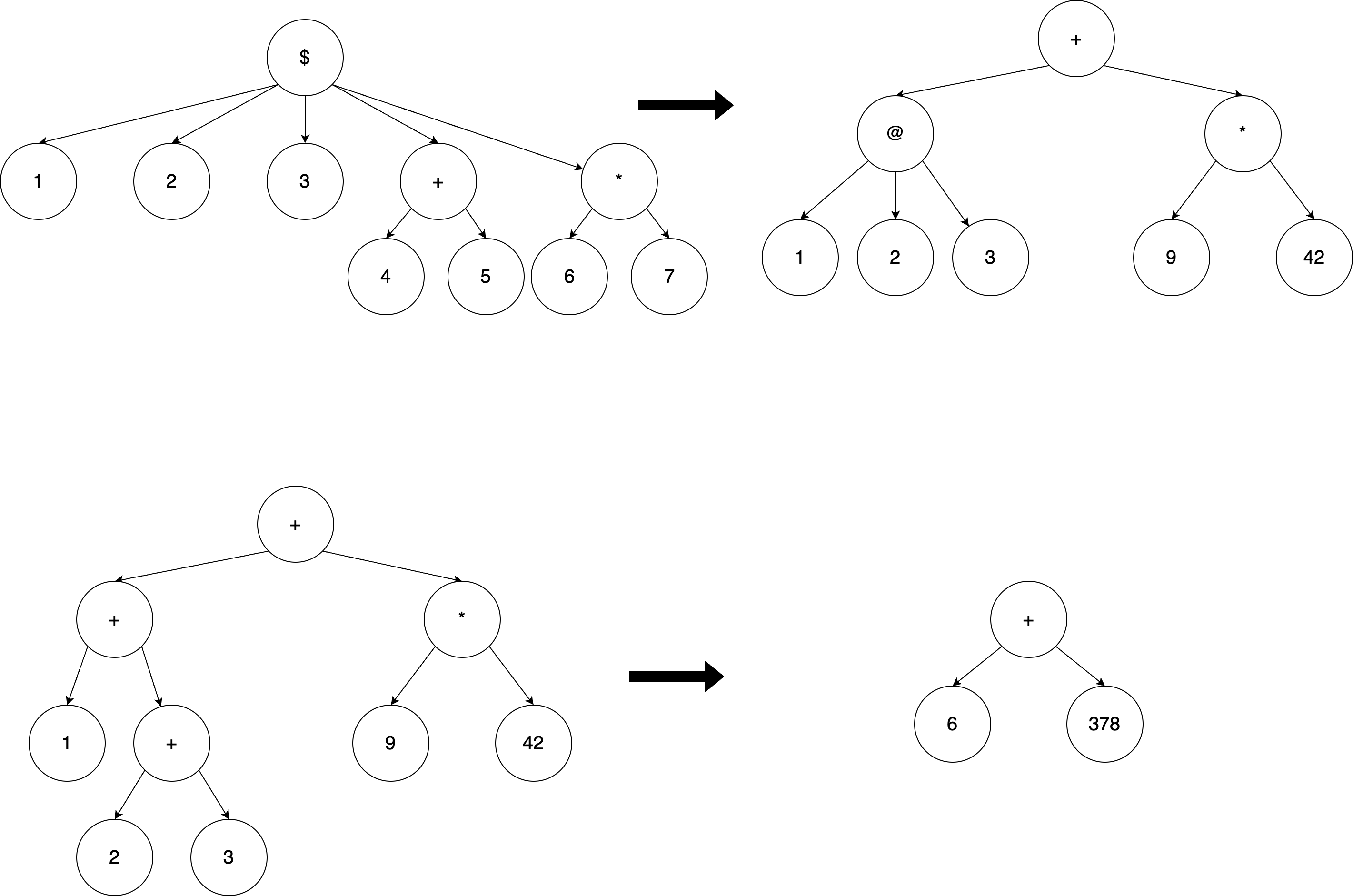
In this case, the custom operator @(A, B, C) computes A + B + C, represented by the preorder traversal + A + B C, and the other custom operator $(A, B, C, D, E) computes @(A, B, C) + (D * E), represented by the preorder traversal + @ A B C * D E
Given the expression 1 2 3 + 4 5 * 6 7, where A = 1, B = 2, C = 3, D = 4 + 5, E = 6 * 7,we break down $ and obtain the syntax tree + @ 1 2 3 + 4 5 * 6 7. Then, we break down @ and get + @ 1 2 3 * 9 42. Finally, we compute the result as 6 + 378 = 384.
The syntax tree can be visualized as:
Next, there are q operations, and each operation can be one of the following:
- Given index, change the value or symbol of a node at positions index in the initial syntax tree’s preorder traversal.
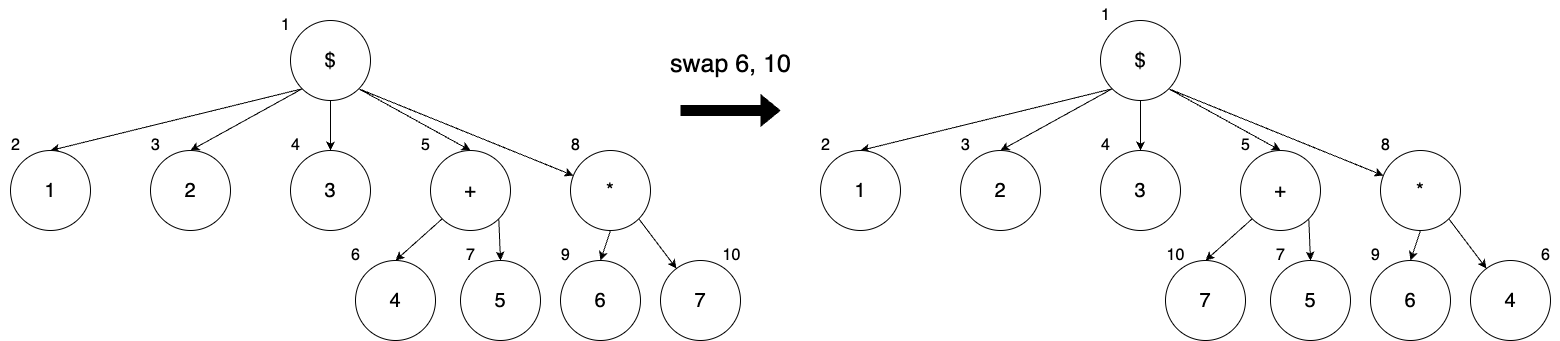
- Given index1 and index2, swap the subtrees of the nodes at positions index1 and index2 in the initial syntax tree’s preorder traversal. Note that after swapping the two nodes, their indices will also be swapped. Refer to the diagram below for clarification.
- Output the result of the syntax tree after calculation.
Input
The first line contains three integers: n, m, and q, which represent the total number of nodes, the number of custom operators, and the number of operations, respectively.
The next m lines describe the custom operators. Each line includes:
- A character oi: the symbol of the i-th custom operator.
- A positive integer ki: the number of input parameters it takes.
- A string si: the preorder traversal result of the syntax tree created by this operator’s rule, made up of numbers and operators (including +, -, *, and operators defined earlier.), with each operator or number separated by a space.
Next line contains a string representing the syntax tree’s preorder traversal result, with each element separated by a space.
The following q lines represent q operations, where each operation can be one of these:
1 index num: Change the number of the node at position index to num.2 index1 index2: Swap the subtrees of the nodes at positions index1 and index2.3: Output the result of the current syntax tree after calculation, modulo 109 + 7.
Constraints
- 1 <= n <= 104
- 0 <= m <= 10
- 1 <= q <= 105
- t and si are made up of numbers and visible characters, and si will contain other custom operators defined earlier.
- 1 <= | si | <= 150
- oi will be a visible character other than
+, -, or* - All numbers are between [0, 109].
- 2 <= ki <= 5
- The number of type 3 operations (output results) is <= 100.
- In the third type of operation, the parents of the two nodes will be different, and the two nodes being swapped will have the same properties (both are numbers, or both are operators that take the same number of parameters).
Subtasks
- testcase 1: m = 0, q = 1, ki = 2, and only the third operation is present.
- testcase 2: m = 0, ki = 2
- testcase 3: q = 1, ki = 2, and only the third operation is present.
- testcase 4 ~ 6: ki = 2
- testcase 7 ~ 8: q = 1, and only the third operation is present.
- testcases 9 ~ 10: No additional constraints.
Output
Whenever the operation 3 is encountered, output the result of the current syntax tree after calculation, modulo 109 + 7. If the result after applying 109 + 7 is negative, add 109 + 7 to it before outputting. You can refer to Example 2: the original calculation result is -69, and after adding 109 + 7, it becomes 999999938.
You can consider modifying the following code to solve this problem: