Description

A decision tree is a popular machine learning algorithm that models decisions and their possible consequences. The tree structure consists of nodes representing attributes, branches representing decision rules controlled by threshold values, and leaf nodes representing labels. For each input to a decision tree, we follow the attribute and its corresponding threshold values to decide which subtree to traverse. Once a leaf node is reached, the input is classified to the label on that node.

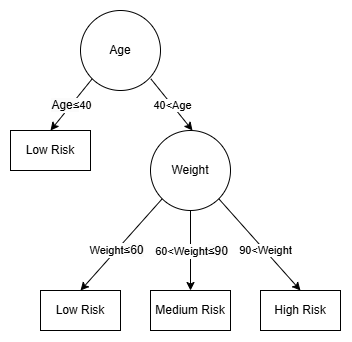
Here is an example:

For simplicity, we define a decision tree as follows:

Attribute  := Non-negative integer  
Label      := Capital letter 
CNT        := Positive integer
Threshold  := Integer
Thresholds := List of Threshold seperated by `,` 
TREE       := Attribute '/' CNT '[' Thresholds ']' {CNT+1}*{'(' TREE ')'} | Label

Attribute are numbered from $0$ to $n-1$ if there are $n$ attributes in total. We use a single capital letter to represent a Label and CNT to represent the number of threshold values at a node. It is guaranteed that there are exactly CNT threshold values in Thresholds and CNT+1 subtrees.

Then the previous example can be modeled as:

1/1[40](B)(0/2[60,90](B)(C)(A))

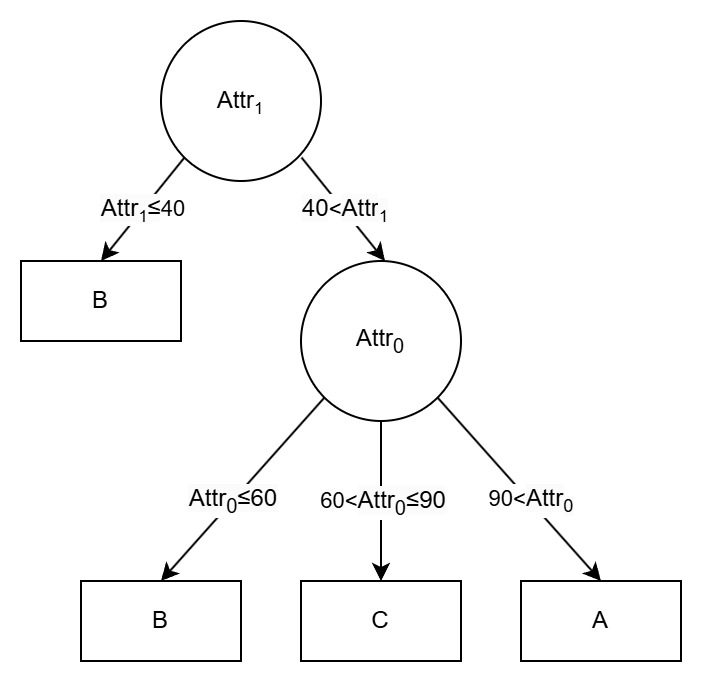
Your task is to classify each input to the decision tree, which is a list of integers where each integer represents the value of an attribute. Here is an example decision tree input if there are three attributes in total, and how to classify this input:

90 45 10

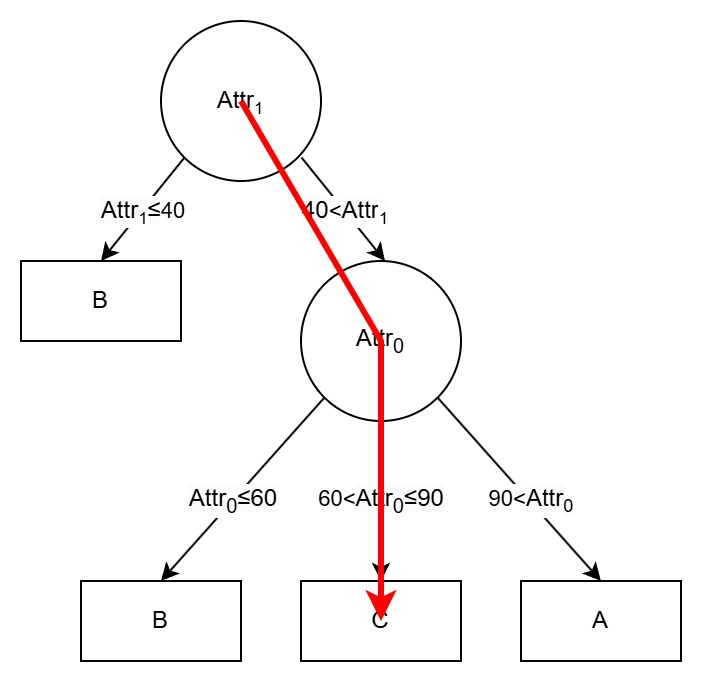
Noted that not every attribute will be used in the decision tree

Input

The first line contains two integers $n$ and $q$, representing the number of attributes and the number of query.

The second line contains a string $S$, representing the decision tree.

The following $q$ lines, each contain $n$ integers, representing the value for each attribute of an input, where $a_{i,j}$ is the $j^{th}$ attribute's value of $i^{th}$ input.

$n \quad q$
$S$
$a_{0,0} \quad a_{0,1} \quad \dots \quad a_{0,n-1}$
$a_{1,0} \quad a_{1,1} \quad \dots \quad a_{1,n-1}$
$\quad\vdots$
$a_{q-1,0} \quad a_{q-1,1} \quad \dots \quad a_{q-1,n-1}$

Constraints

• $1 \leq n \leq 100$
• $1 \leq q \leq 5000$
• $1 \leq |S| \leq 10^6$
• $1 \leq$ CNT $\leq 5$
• $-10000 \leq$ Threshold $\leq 10000$
• $0 \leq$ Attribute $< n$
• Label is a single capital letter.
• Threshold values in one node are unique and sorted in increaing order

Output

Output $q$ lines, each containing only one capital letter, the classified label of each input to decision tree.

Sample Input  Download

Sample Output  Download

Tags

Discuss