Description
This is a multi-testcase problem. You need to solve \(q\) testcases.
Procat has some maps. But some of them are duplicated. For each testcase, he will give you two of them, labeled \(X\) and \(Y\), hoping you could determine whether they are the same or not.
Each map is a rooted tree. The tree consists of \(N\) vertices, numbered from \(1\) to \(N\). There are exactly one simple path between any two vertices.
Procat will give you the map in a special format. The format is described by the following EBNF (Extended Backus–Naur form):
TREE ::= INT "(" TREE ")" "(" TREE ")"
| NIL
It means that a tree is a integer followed by two subtrees or a NIL. The integer represents which vertex the root of the tree is. If the tree is a NIL, it means that the tree is empty.
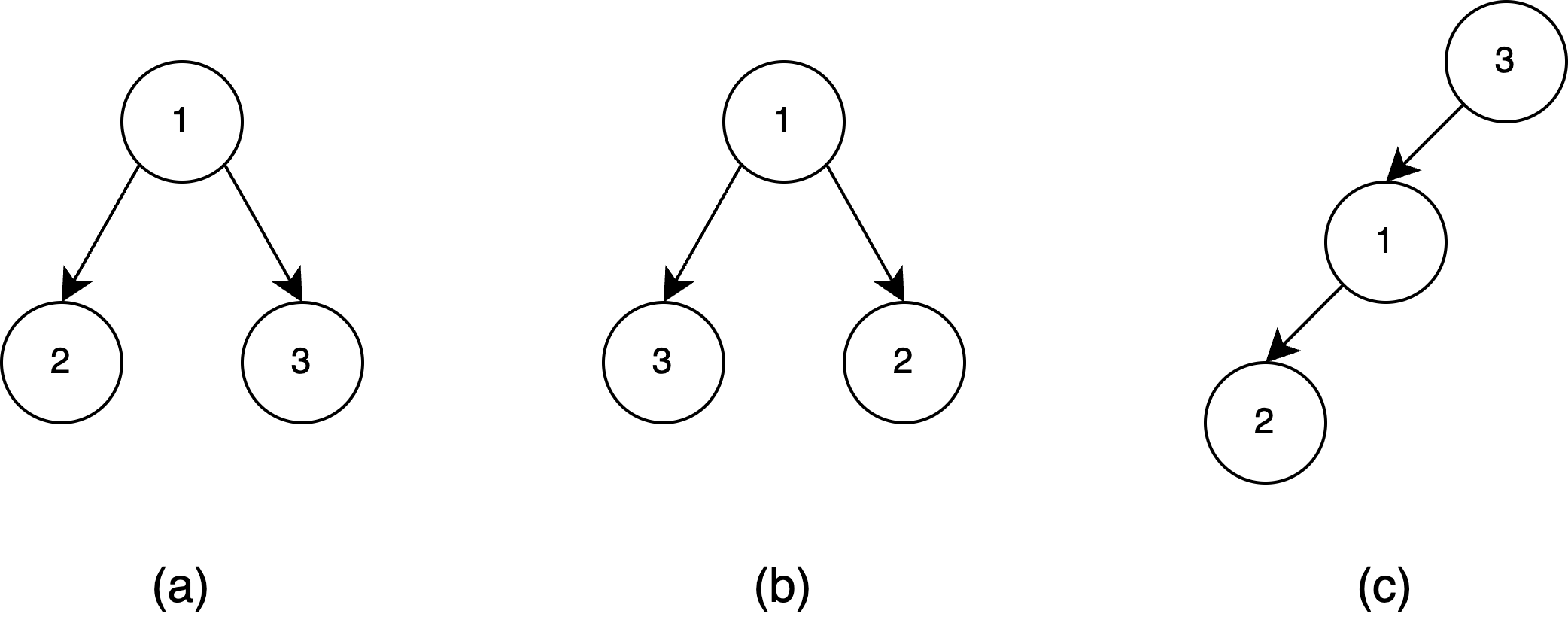
Let’s look at some examples. In the figure below, tree (a) will be represented as 1(2()())(3()()), tree (b) as 1(3()())(2()()), and tree (c) as 3(1(2()())())(). However, only tree (a) and tree (b) are considered the same.
Two maps are considered the same if and only if they have the same root and for every pair of vertices \((u, v)\) \((1 \le u, v \le N)\), which means the path from \(u\) to \(v\) in the first map is the same as the path from \(u\) to \(v\) in the second map.
Input
The first line contains an integer \(q\), the number of testcases.
For each testcase, the first line contains an integer \(N\), the number of vertices in each map. The following two lines contain two strings, representing map \(X\) and \(Y\) respectively in the EBNF format.
\(N\) \(X\) \(Y\)
Constraints
- \(1 \leq N \leq 10^5\)
- length of \(X\) and \(Y\) won’t exceed \(10^6\) characters
- \(X\) and \(Y\) only contains characters
(,)and digits.
Output
For each testcase, output YES if the two maps are the same, otherwise output NO.
You need to output a newline after each answer.