Description
Given an adjacency matrix of a directed graph with n vertices, compute its transitive closure.
An adjacency matrix A of a directed graph with n vertices is an n x n matrix where:
- a[i][j] = 1 if there is a direct edge from vertex i to vertex j.
- a[i][j] = 0 if there is no direct edge from vertex i to vertex j.
The transitive closure of a directed graph is another n x n matrix B, where:
- b[i][j] = 1 if there exists a path (direct or indirect) from vertex i to vertex j.
- b[i][j] = 0 if there is no path from vertex i to vertex j.
The goal is to compute the matrix B, representing the transitive closure of the graph.
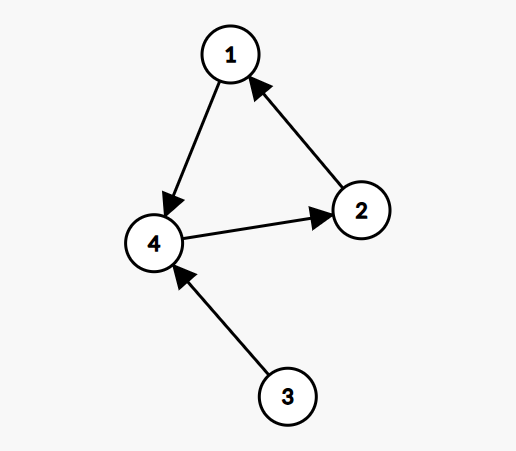
(Graph from sample input)
Input
The input consists of n+1 lines:
- The first line contains a positive integer n, where 1 ≤ n ≤ 1000 (the number of vertices in the graph).
- The next n lines contain n integers each. The i-th row and j-th column contains the value a[i][j], which is either 0 or 1
Output
The output should consist of n lines:
Each of the n lines should contain n integers, where the i-th line and j-th column should contain the value b[i][j] from the transitive closure matrix.