Description

In the previous mission, Bee Agent User333 performed excellently, so he has now been dispatched on a mission to Pollen Kingdom, an ally of Honey Kingdom.

Pollen Kingdom, a nation established by butterflies, also organizes its areas in a regular hexagonal (正六邊形) pattern due to historical reasons. This means the map of Pollen Kingdom consists entirely of hexagonal cells.

To facilitate development, they use a unique coordinate system where each hexagonal cell is represented by coordinate (x,y) as shown below:

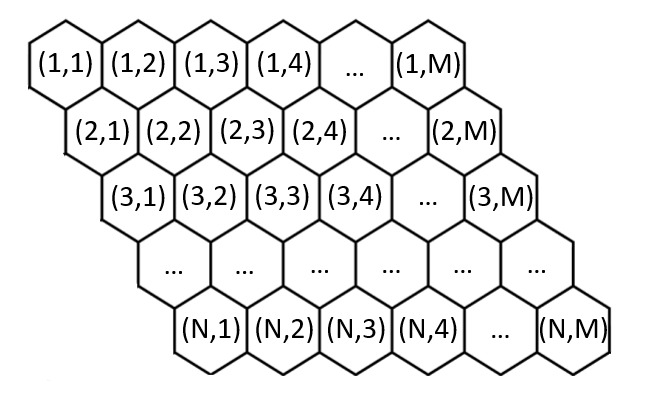
The map is structured such that the first row has coordinates:

(1,1) , (1,2) , ... , (1,M)

The second row then has:

(2,1) , (2,2) , ... , (2,M)

...

In this system, each cell (x,y) is positioned between (x−1,y) and (x−1,y+1).

For any cell located at (x,y), its neighboring cells are:

(x-1,y) , (x-1,y+1) , (x,y-1) , (x,y+1) , (x+1,y-1) , (x+1,y)

Agent User333 has been assigned T missions, each with a different map. On each map, the starting point is always (1,1), and the destination is (N,M).

Each cell on the map contains specific information represented by A_i,j ​:

• If A_i,j = 'X', the cell is mostly water. For safety reasons, User333 cannot travel across water.
• If A_i,j = '0', the cell is open grassland, which User333 can freely cross.
• If A_i,j is a number between '1' and '5',it indicates the presence of a "magic circle" with a "teleport radius" A_i,j​. Standing on this magic circle allows the agent to teleport to any cell within A_i,j​ steps, ignoring obstacles like water while moving, but they cannot teleport directly onto water cells. 

  Whenever User333 arrive at a magic circle, you can choose one of the following options:

  • Spend one bottle of potion to use the magic circle's teleportation ability.
  • Don’t spend any potion and treat it as an open grassland cell.

Agent User333 has been assigned T missions, each with a different map. On each map, the starting point is always (1,1), the destination is (N,M), and he has C bottles of magic potion for that mission.

Input

The first line of input contains a positive integer T, representing the number of maps.

For each map, the input is structured as follows:

• The first line contains three positive integers, N, M, and C, representing that this is an N × M map and that User333 has received C bottles of magic potion for this mission (note: unused bottles cannot be carried over to the next mission; each mission has a separate allocation of potions).

• The next N lines each contain M entries:

  A_1,1 , A_1,2 , ... , A_1,M
  ​A_2,1 , A_2,2 , ... , A_2,M
• Each entry A_i,j can be:
  • 'X' for water (impassable).
  • '0' for open grassland (passable).
  • A number between '2' and '5' for a magic circle with that radius.

Constraints

• 1 ≤ T ≤ 10
• 1 ≤ N,M ≤ 500
• 0 ≤ C ≤ 100
• A_i,j ∈ { 'X'  , '0' , '2' , '3' , '4' , '5' }
• Each map has at most 100 magic circles.
• The starting point (1,1) and the destination (N,M) are guaranteed to be open grassland.

Subtasks

• Testcases 1~2: N = 1, and there is no magic circle in the map.
• Testcases 3~4: N,M ≤ 10, and there is no magic circle in the map.
• Testcases 5~6: there is no magic circle in the map.
• Testcases 7~8: A_i,j ∈ { 'X'  , '0' , '2' , '3' } ; C = 100
• Testcases 9~11: C = 100
• Testcases 12 : C = 1
• Testcases 13 : C = 2
• Testcases 14: No additional restrictions.

Hint:

• For testcases 1 ~ 6: You only need to consider whether you can reach the goal; you don't need to worry about the magic circles.
• For testcases 7 ~ 11: You don't need to worry about the number of potions you have; they are sufficient for you to use all the magic circles.

Output

For each map, output a single line containing "YES" if it is possible to reach the destination from the start point, and "NO" otherwise (without quotes).

Please remember to print "\n" at the end of each line.

Sample Input  Download

Sample Output  Download

Tags

Discuss