Description

Given n rectangle R_i, i = 1, 2, ..., n in the Euclidean plane. The lower left point and upper right point of R_i is (0, 0) and (u_i, r_i) repectively.

Find the number of pairs (i, j) such that R_i can be contained in R_j after rotating 90^o or 0^o. Formally speaking, find the number of pairs (i, j) that satisfy at least one of the following conditions:

• u_i ≤ u_j and r_i ≤ r_j
• u_i ≤ r_j and r_i ≤ u_j

For example, the following two rectangles satisfy the condition, since the blue rectangle can be contained in the red rectangle by rotating 90^o (see picture on right hand side).

      

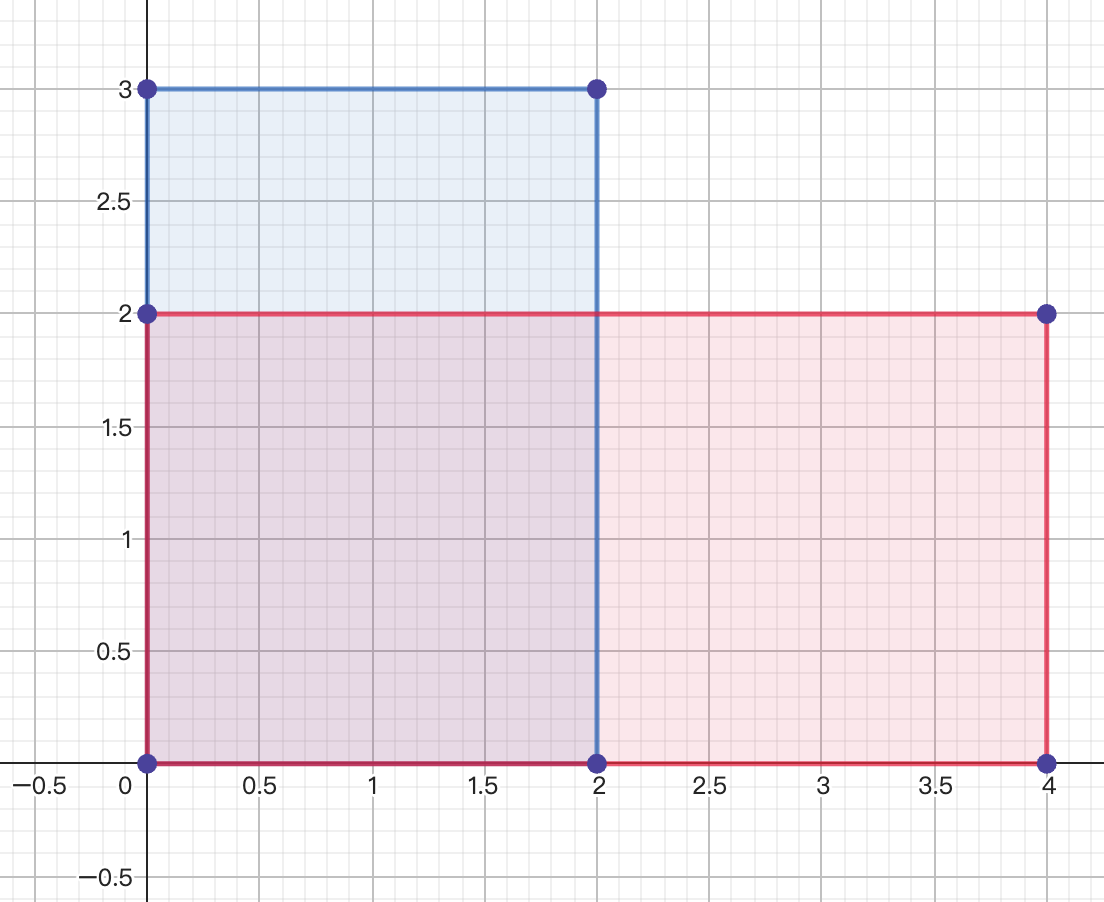
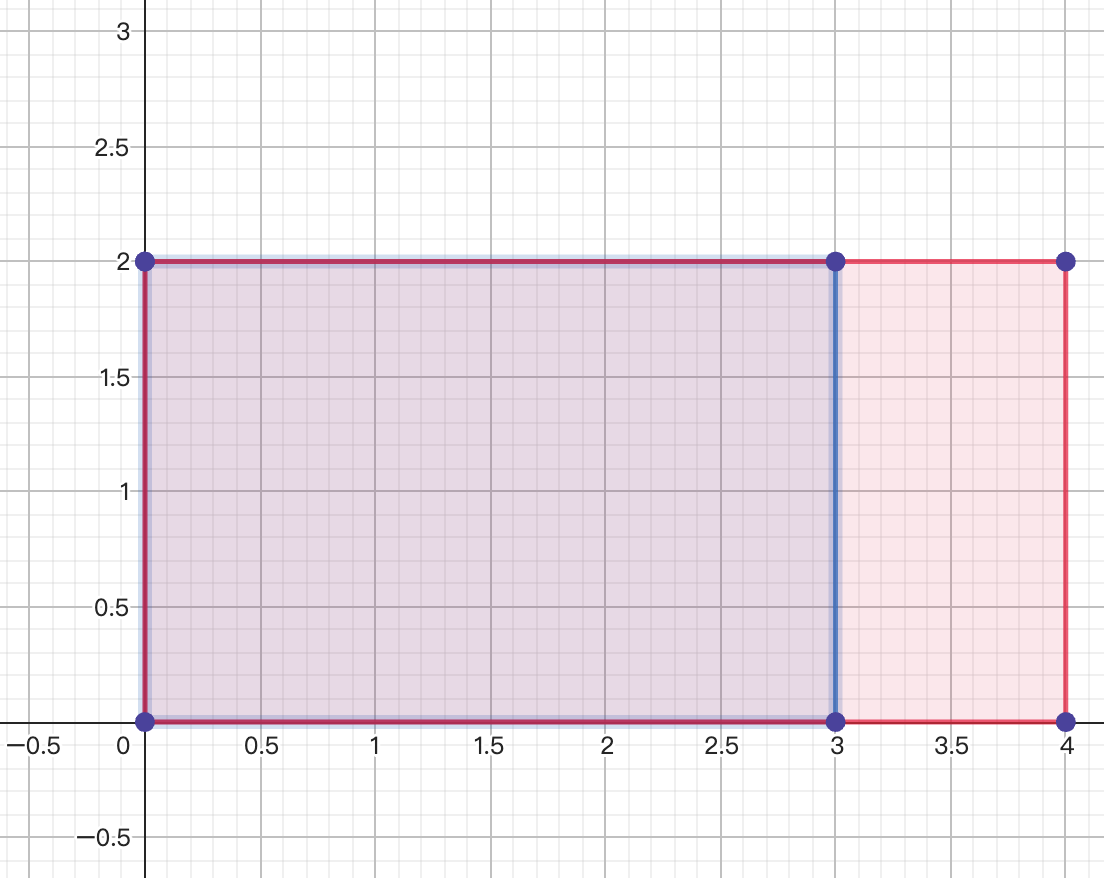
Input

The first line contains an integer n. For the next n line, each line contains two integers u_i, r_i, i = 1, 2, ..., n.

Constrain

• 1 ≤ n ≤ 10⁵
• 1 ≤ u_i, r_i ≤ 10⁹, i = 1, 2, ..., n
• No two rectangles are identical after rotating 90^o or 0^o.

Output

Output one integer: the number of pairs satisfying the condition above.

Sample Input  Download

Sample Output  Download

Tags

Discuss