Description

Notice. Some of the TODOs are identical to those in Part 1: Tic-tac-toe (these are marked with TODO_xx in function.h). If you have already completed Part 1: Tic-tac-toe, you can copy the solution from Part 1 and further implement the remaining 3 TODOs in this problem (Board::Board(const Board& b), Board& Board::operator=(const Board &b) and TetrisBoard& TetrisBoard::operator+=(const Move& m)).
Your task is to adapt the framework that supports board games to also support another classic game, Tetris (俄羅斯方塊).
To simplify the problem, we will modify the rules of Tetris. In Tetris, players drop differently shaped blocks that descend onto the playing field, and the game ends when the blocks exceed the top of the playing field. (Tips for those familiar with Tetris: In the original version of game, completed lines disappear; however, in this version, they won't disappear)
We are interested in determining how many blocks can be dropped given a sequence of blocks with specific rotations and dropping positions.
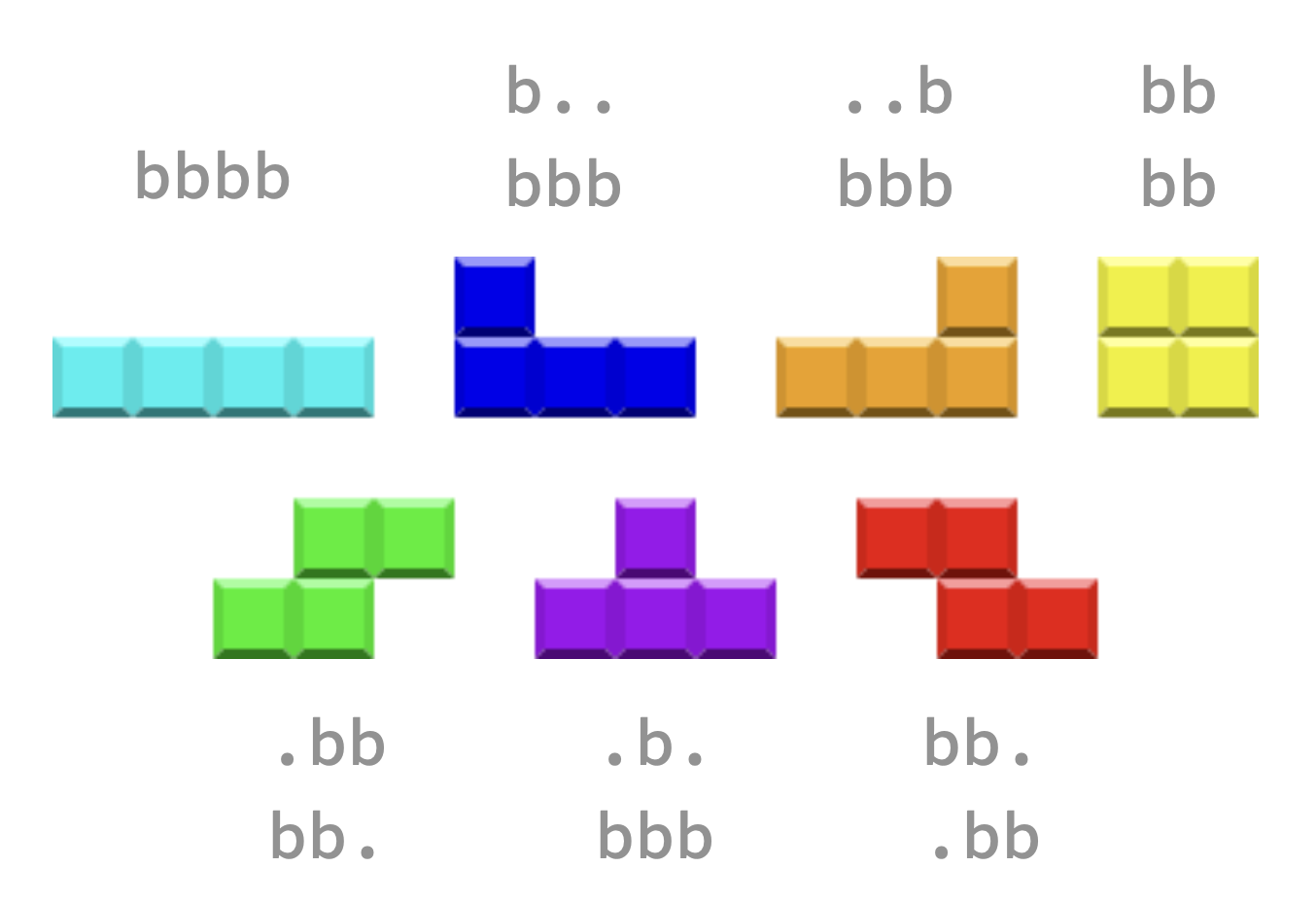
There are 7 types of blocks, each represented by '.' and an arbitrary lowercase letter.
The following GIF illustrates the 1st sample I/O.
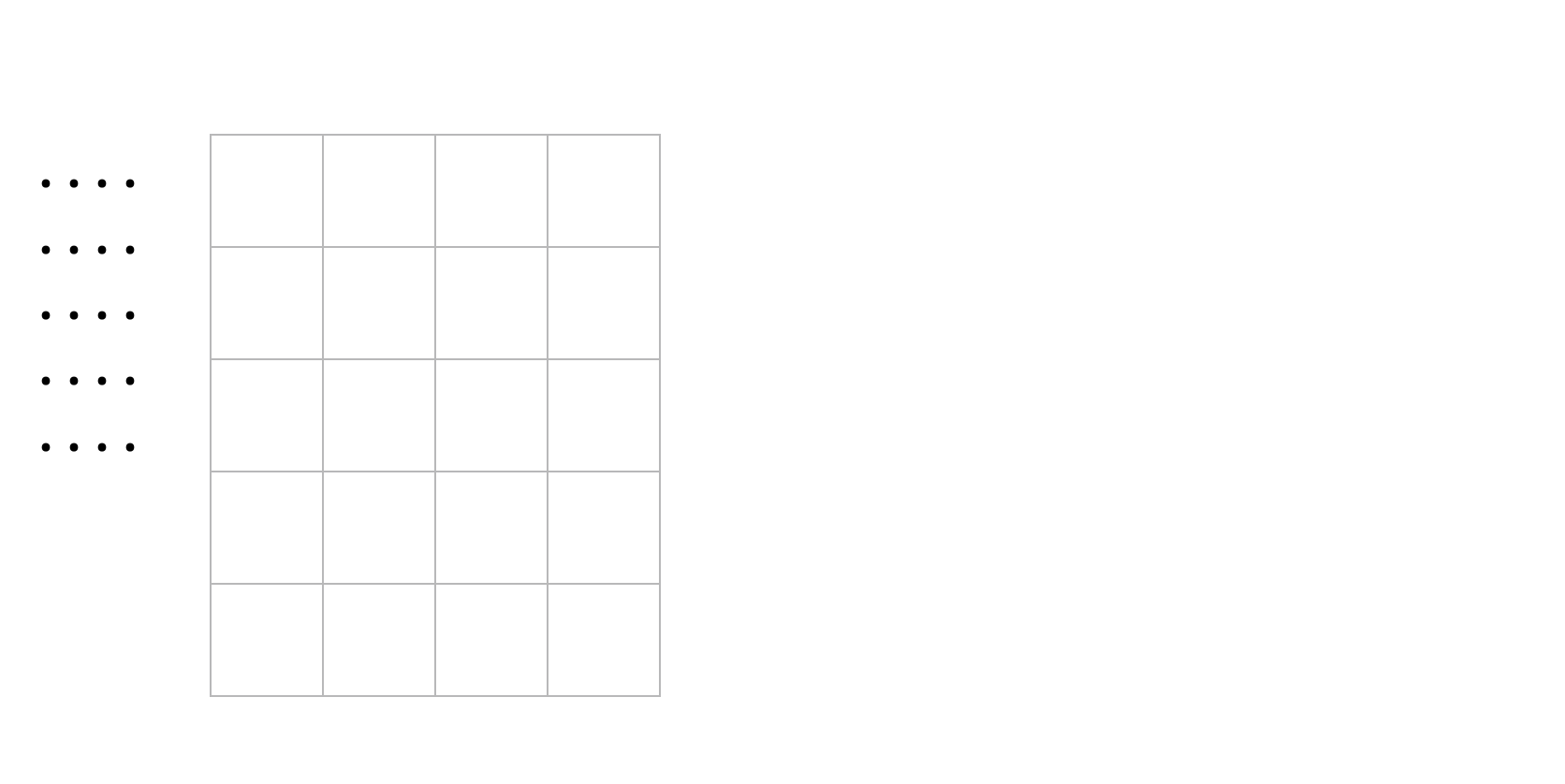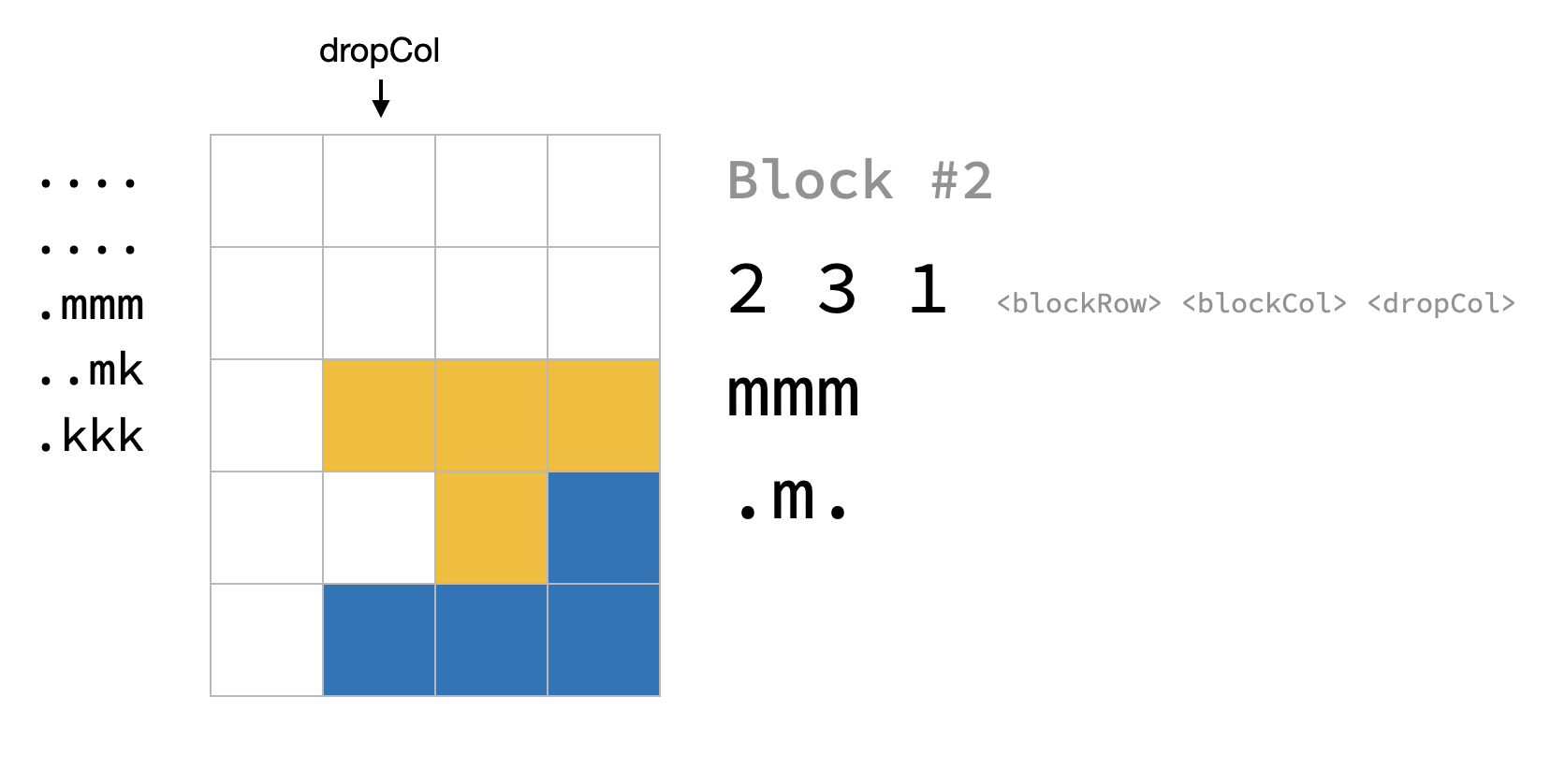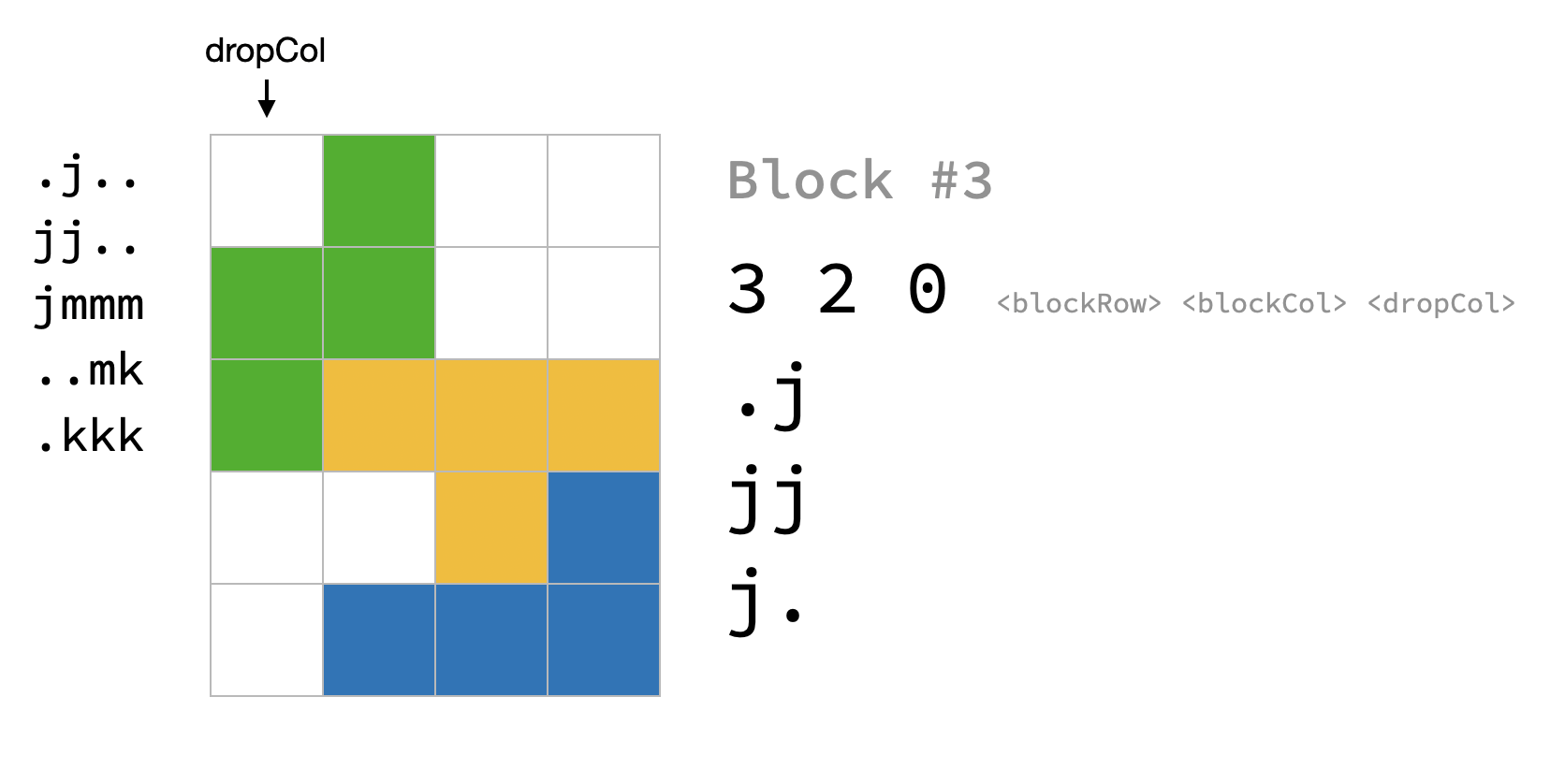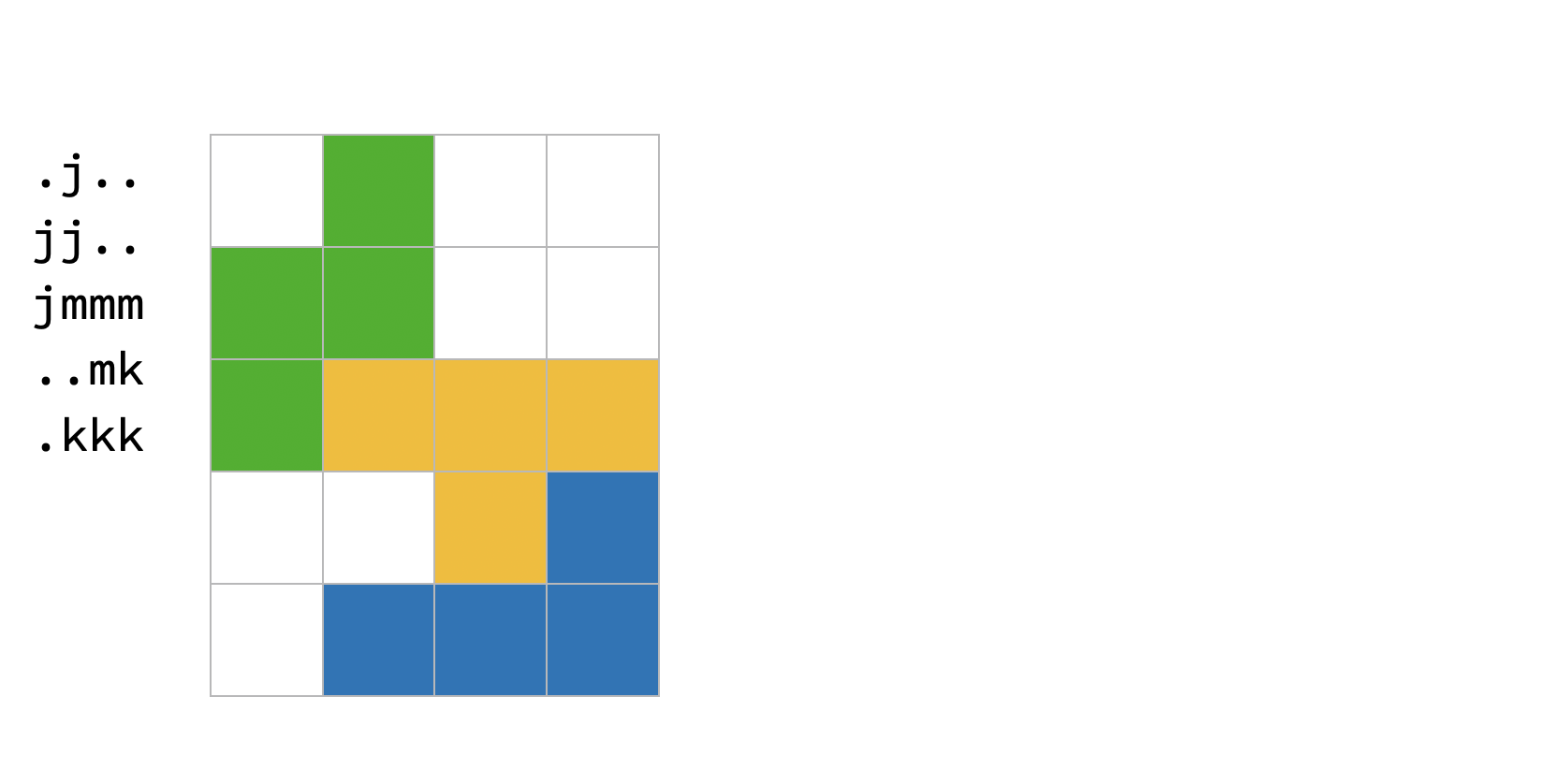
This is a partial judge problem. Please review the provided code and refer to the sections labeled "TODO" in the function.h file for further details, and using C++17 to submit your solution.
Input
The first line of the input contains an integer N, representing the number of test cases (1 ≤ N ≤ 5,000).
For each of the N test cases, the first line contains two integers, x and y (4 ≤ x, y ≤ 20), representing the height and width of the playing field, respectively. This is followed by a sequence of blocks to be dropped.
Each block in the sequence is preceded by three integers: bx, by, and c, where bx and by denote the height and width of the block, and c indicates the leftmost column position for dropping the block. Each block is represented by '.' and an arbitrary lowercase letter (stored in a vector<string>; please review the provided code). The sequence or test case ends when bx = by = c = 0.
We guarantee that the position for dropping the block will not exceed the width of the playing field.
Test Case Constraints
- Testcases 1, 2: For these test cases, only the following block will be given as input:
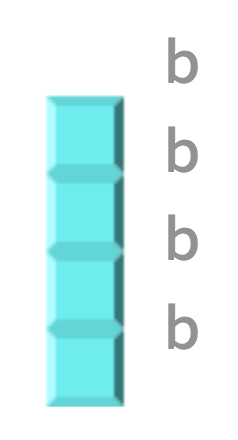
Since there is only one possible block, we provide a trivial implementation ofTetrisBoard::operator+=for your reference. You can simply paste the code to pass the two test cases.
int rows = getRows(), dc = m.getDropColumn(), st_row = rows - 4;
for (int i = 0; i < rows; ++i) {
if ((*this)[i][dc] != '.') {
st_row = i-4;
break;
}
}
if (st_row < 0) isGameEnd = true;
else {
for (int i = 0; i < 4; ++i) {
(*this)[st_row+i][dc] = m.getBlock()[i][0];
}
}
return *this;
}
- Testcases 3, 4: For these test cases, only the following blocks will be given as input:
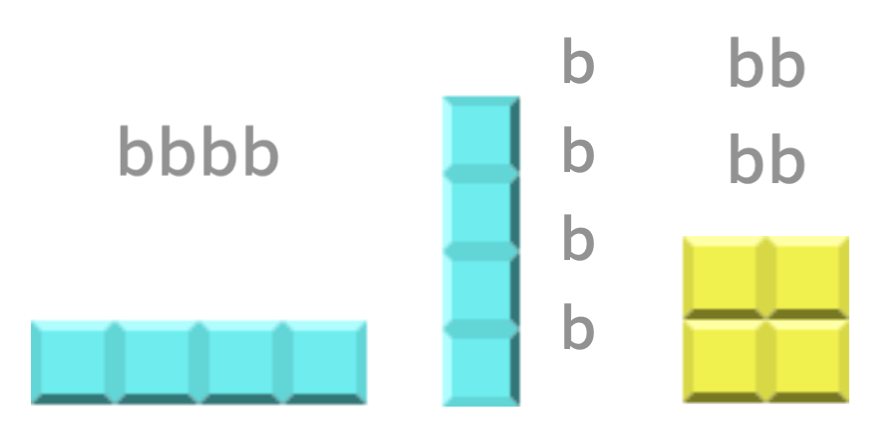
- Testcases 5, 6: All seven blocks can be dropped in rotations of 0, 90, 180, and 270 degrees.
Output
Output the playing field as shown in the sample output provided.