Description
"Run?"
"Who's running?"
"Running where?"
"And why?!" said Shadow sama. At the same time, Shadow sama spreads his mana all over Midgar Kingdom.

"Observe!"
"And witness for yourselves!"
"Supremely ultimate, almighty and unparalleled attack!"
"I..."
"...am..."


Beta (one of the Seven Shadows, higher-ups of Shadow Garden), who is keen on writing down feats of Shadow sama, is stunned by the sight of Shadow Sama's attack, and missed the chance to record it.


Beta has the map of Midgar Kingdom, which is a tree with \(N\) nodes, numbered from \(1\) to \(N\). Shadow Sama is at one of the nodes as he spreads his mana. With \(k\) unit of mana, Shadow Sama can cover the node he is at, and all the nodes that are at most \(k\) edges away from him.
Beta knows that Shadow Sama is so smart that he must have chosen the place he was at wisely, and spent the least amount of mana to cover the whole Midgar Kingdom. Sasuga Shadow Sama!
However, since Shadow Sama's attack is so breathtaking, Beta forgot to record the details of it. In order to demonstrate Shadow Sama's wisdom, you need to calculate the minimum amount of mana required for him to cover the whole Midgar Kingdom.
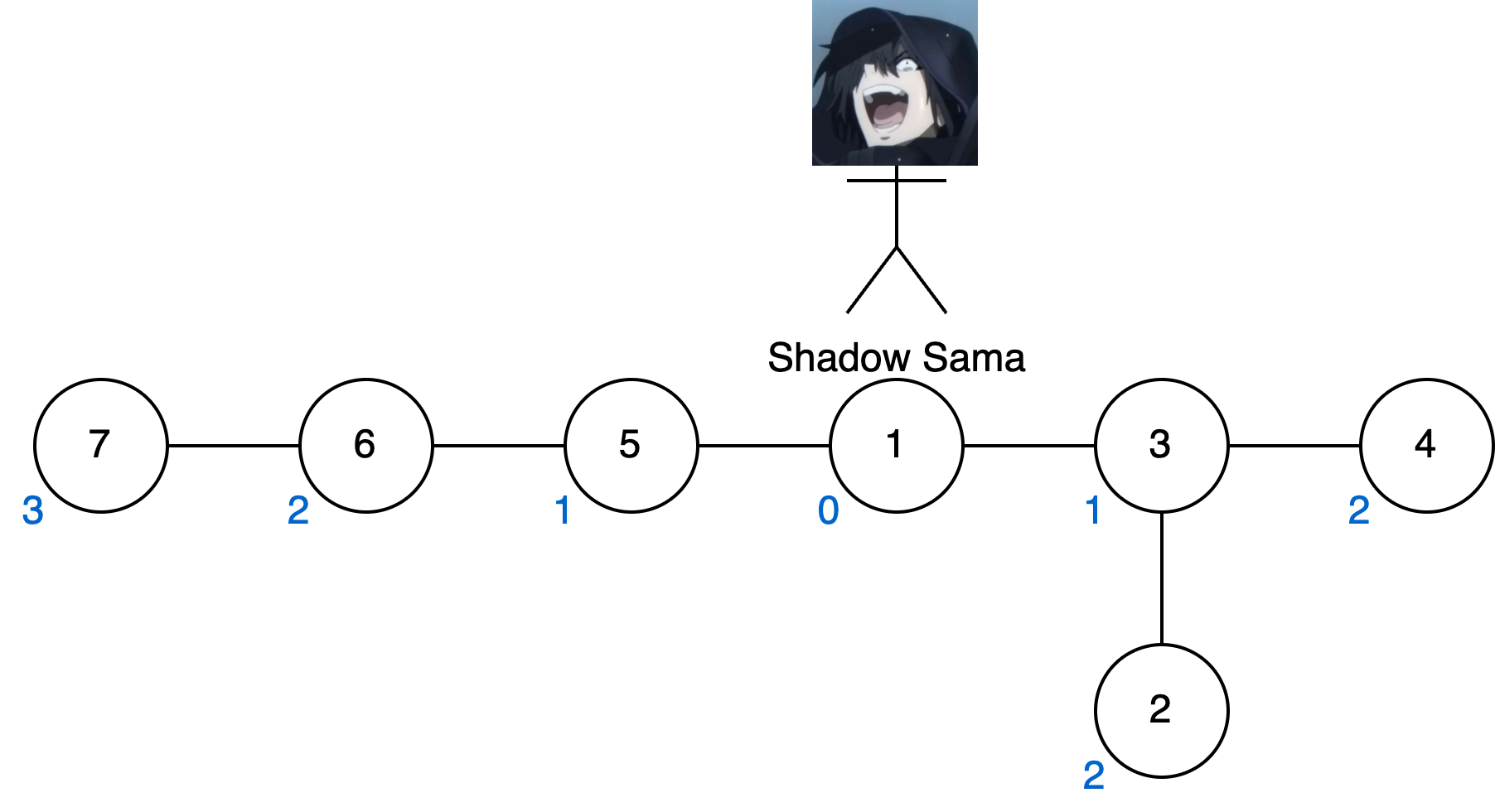
For the sample test case, we can draw the tree as shown below. When Shadow Sama is at node #1 (or node #5), he can cover all the nodes with 3 units of mana.
Input
The first line contains an integer \(N\), the number of nodes in the tree.
For the following \(N-1\) lines, each line contains two integers \(u_i\) and \(v_i\), indicating that there is an bidirectional edge between node \(u_i\) and node \(v_i\).
\(N\)
\(u_1 \quad v_1\)
\(u_2 \quad v_2\)
\(\vdots\)
\(u_{N-1} \quad v_{N-1}\)
Constraints
- \(1 \leq N \leq 10^5\)
- \(1 \leq u_i, v_i \leq N\)
- The input is a tree.
Output
Output contains one line with an integer, the minimum units of mana required to cover the whole Midgar Kingdom.
You don't have to print spaces or newlines at the end of the line.