Description
Today is your birthday, your father wants to prepare a gift for you. He ranks his brains and finally decides what to give. Since you are a college student major in computer science, he gives you a rooted binary tree for your birthday! But at the time you are unpacking the gift, you accidentally damage the binary tree! What a pity! You have tried very hard to restore the information of the binary tree but end up failure. For each node, you know which two nodes are its children, but you don't know which one is left child and which one is right child.
Fortunately, your father told you this is a binary search tree (BST) originally, and you want to know whether the broken information of the binary tree is possible to reconstruct the original binary search tree (BST) and get its inorder traversal sequence.
Note: the value of each node is same as its index in this problem.
What is a Binary Search Tree?
A binary search tree (BST) is a binary tree data structure with the following properties:
- Each node in the tree has at most two child nodes (binary tree).
- For any node, its value is greater than or equal to the values stored in the left subtree.
- For any node, its value is smaller than the values stored in the right subtree.
- For any node, the left subtree and the right subtree are binary search trees respectively as well.
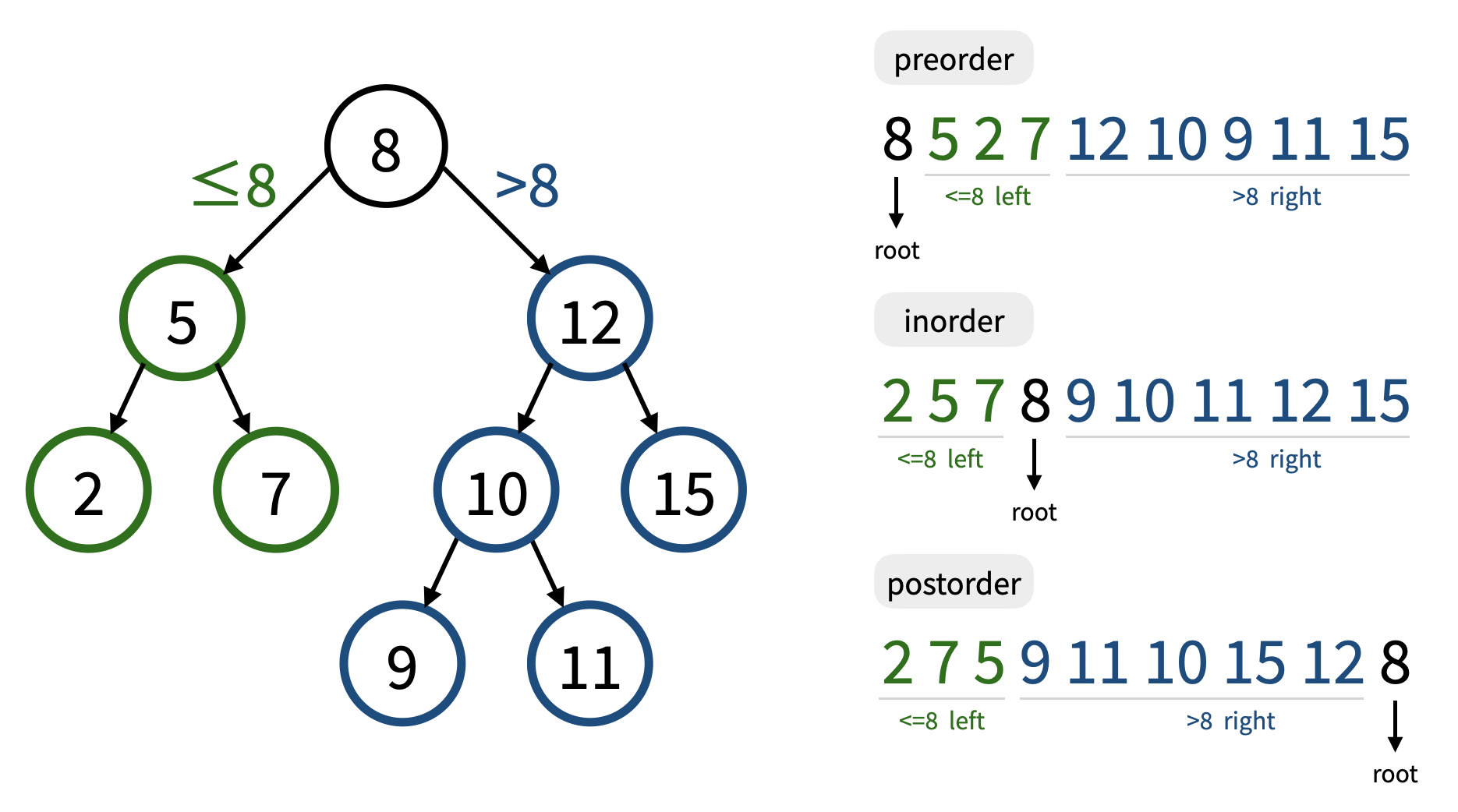
Hint: observe what is special about BST's inorder traversal.
Input
The input contains T testcases.
The first line of each testcase contains a single integer N, representing the number of nodes in the binary tree.
The indices of nodes in the binary tree are 1-based, ranging from 1 to N, and the value of each node is same as its index in this problem.
For the following N lines, each line contains two integers. For i-th line, the two integers represent the children of i-th node. 0 represents that the node doesn't exist.
Constraint of testcases:
for all testcases: 1 ≤ N ≤ 100000, 1 ≤ T ≤ 10
Testcase 1: the answer is always "YES", and when input the children of each node, the first one is always the left child, the second one is always the right child (You just need to print the inorder traversal of the tree).
Testcases 2, 3: the answer is not always "YES". but when input the children of each node, the first one is always the left child, the second one is always the right child (You just need to print the inorder traversal of the tree).
Testcases 4, 5: No additional constraint.
Output
For each testcase, if there exists a way to distribute nodes to left child or right child that it becomes a BST, then output "YES" otherwise "NO".
If the answer is yes, please output the inorder traversal of the tree in the next line. Otherwise, don't ouput anything in the next line.
Remember to add a newline character at the end of every line, and there is no spaces at the end of line.