Description
Procat (aka Procastinator Cat) has some maps. But some of them are duplicated. He will give you two of them \(X\) and \(Y\), hoping you could determine whether they are the same or not. However, Dogeon (aka Doge the Pigeon) has eaten part of the maps. Fortunately, Dogeon only ate all the empty brackets (i.e. ()), so the structure of the maps is still preserved.
Each map is a rooted tree. The tree consists of \(N\) vertices, numbered from \(1\) to \(N\). There are exactly one simple path between any two vertices.
Procat will give you the eaten map in a special format. The format is described by the following EBNF (Extended Backus–Naur form):
TREE ::= "(" INT TREE TREE ")"
| "(" INT TREE ")"
| "(" INT ")"
It means that a tree is a integer followed by no more than two subtrees. The integer represents the value of the vertex. If there is no subtree, it means the vertex is a leaf. Otherwise, the first subtree is the left child and the second subtree is the right child.
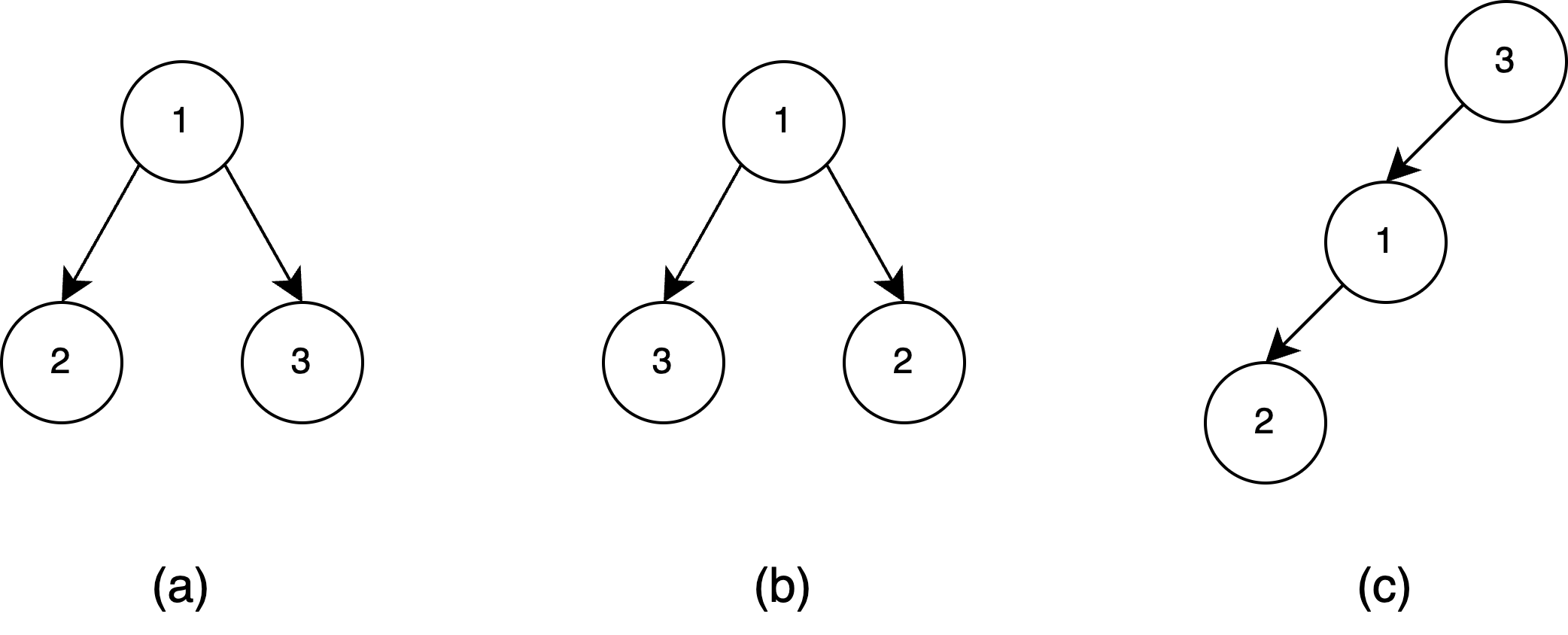
Let's look at some examples. In the figure below, tree (a) will be represented as (1(2)(3)), tree (b) as (1(3)(2)), and tree (c) as (3(1(2))). However, only tree (a) and tree (b) are considered the same.
Two maps are considered the same if and only if they have the same root and for every pair of vertices \((u, v)\) \((1 \le u, v \le N)\), which means the path from \(u\) to \(v\) in the first map is the same as the path from \(u\) to \(v\) in the second map.
Input
The first line contains an integer \(T\), the number of subtasks of the testcase. For all subtasks:
-
First line contains one integer \(N\) indicates the number of vertices in each map.
-
Each of the following two lines contains a string, representing map \(X\) and \(Y\) respectively in the EBNF format.
\(N\)
\(X\)
\(Y\)
Constraints
- \(1 \leq T \leq 5\)
- \(1 \leq N \leq 10^5\)
- length of \(X\) and \(Y\) won't exceed \(10^6\) characters
- \(X\) and \(Y\) only contains characters
(,)and digits.
Output
For each subtask, output one line containing "YES" if the two maps are the same, otherwise output "NO". Print a newline character after each line.