Description
Dogeon likes everything to be perfect, just like himself. When Dogeon learned about the data structure: Tree, he hoped every tree would be a perfect BST (binary search tree).
A perfect BST is a type of binary tree, in which every internal node has exactly two child nodes, and all the leaf nodes are at the same depth. What's more, every value stored in the left subtree's nodes will be less than the root's value, and every value stored in the right subtree's nodes will be greater than the root's value. For example, the tree shown below is a perfect BST.
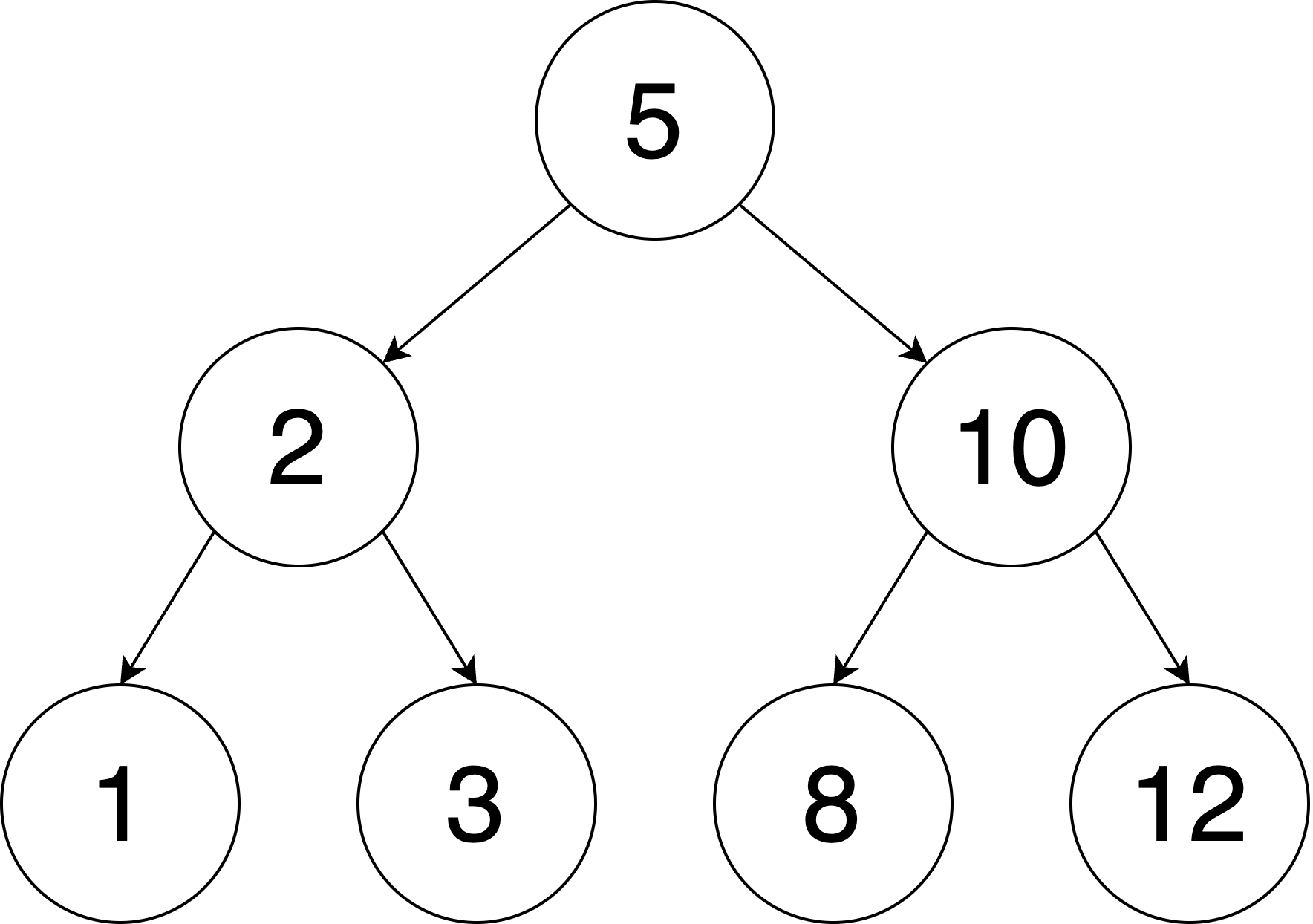
One can easily observe that a perfect BST has exactly $2^k-1$ nodes. Now you will be provided a list of $2^k-1$ numbers, and you should work with Dogeon to construct the perfect BST out of these numbers. Since Dogeon knows that your previous lab has been tough, he will only give you two tasks:
int* pickPivot(int* begin, int* end)- Given pointers to the begin and one after the end of an array, you should select a number from the array and return a pointer to it. Dogeon will do a quick sort on the array based on the pivot you selected.printPostorder(int *begin, int n)- Given pointers to the begin of a sorted array and its length, you should print the post-order traversal of the perfect BST.
- Hint: Is it possible to not build the actual tree?
Input
The first line contains an integer $N$, which is the size of the list.
The second line contains $N$ unique integers $a_1, a_2, a_3,\dots$, which are the elements of the array.
$N$
$a_1 \quad a_2 \quad a_3 \quad \dots \quad a_N$
Constraints
- $N = 2^k-1$, where $k$ is a natural number $(1,2,3,...)$
- $N \le 10^6$
- $-10^9 \le a_i \le 10^9$
Output
The output contains one line, the post-order traversal of the perfect binary search tree. Print a space after each number. You don't need to print a newline at the end.