Description
Procat (破貓) has a lot of electrical appliances in his dormitory, such as computer, refrigerator, and electric fan. He wants to connect all the appliances to the power outlet. There is only one power outlet in his dormitory, so he needs to use extension cords and power strips to connect all the appliances to the power outlet.

Extension cords and power strips Procat currently using don't have overcurrent protection. As a friend of Procat, you are very concerned about electrical safety. You want to help Procat to connect all the appliances to the power outlet in a safe way. Luckily, you have some spare power strips with overcurrent protection. But you don't have any spare extension cords.
Power strips you have got one input and two outputs. Power strips can connect to extension cords, but power strips cannot directly connected to each other.
The price of the high-quality extension cord you want to buy is proportional to the current flowing through it. You wants to minimize the total price of the extension cords you needs to buy.
Calculate total price of the extension cords you need to connect all the appliances to the power outlet.
- After connecting all the appliances to the power outlet, it should look like a binary tree. The power outlet is the root of the tree, and the appliances are the leaves of the tree. The power strips are the internal nodes of the tree. The extension cords are the edges of the tree.
Sample
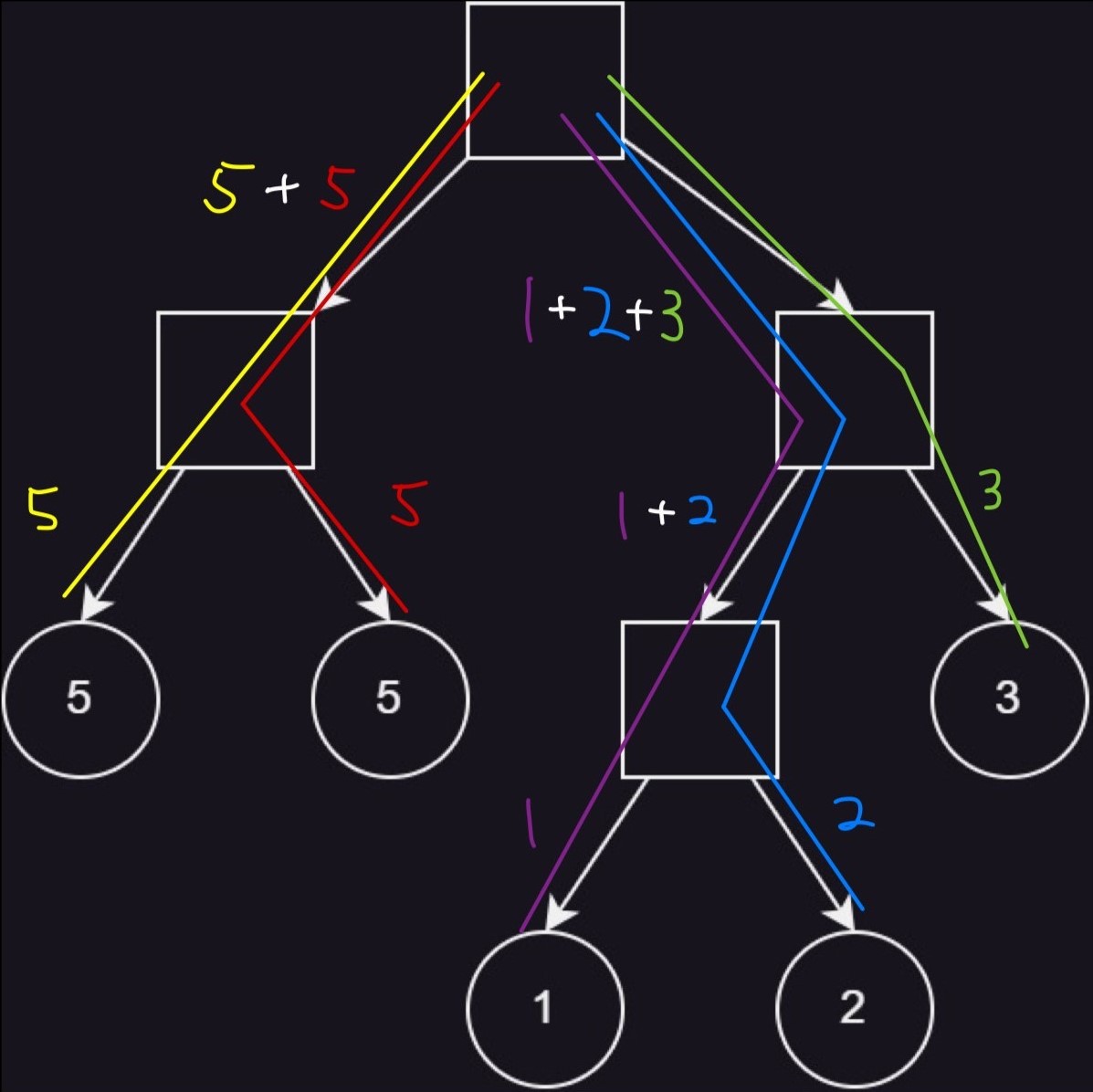
Following figures show examples of optimal ways to connect the appliances to the power outlet in each sample testcase. In each figure, squares represent power strips, circles represent appliances, and edges represent extension cords. The total price of the extension cords is the sum of current flowing through all the edges.
Sample testcase 1:
Sample testcase 2:
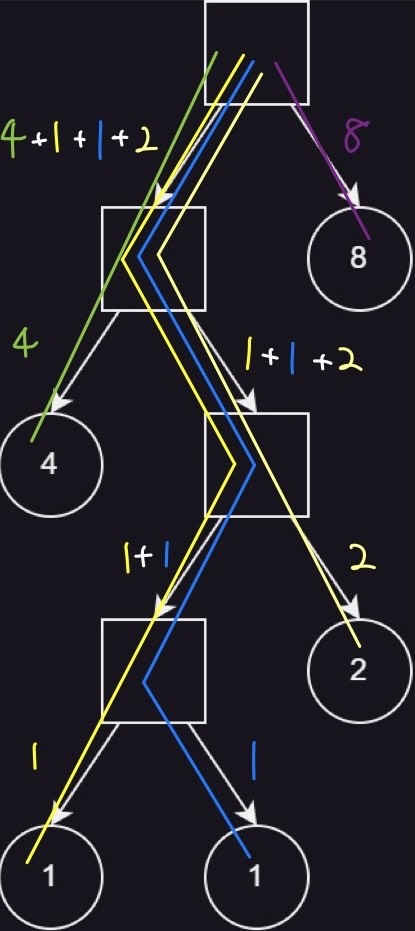
- Hint: Huffman Coding
Input
First line contains an integer \(N\), the number of electrical appliances Procat wants to connect to the power outlet.
The second line contains \(N\) integers \(a_1, a_2, \dots, a_N\), the power consumption of the \(N\) electrical appliances.
\(N\)
\(a_1 \quad a_2 \quad \dots \quad a_N\)
Constraints
- \(1 \leq N \leq 10^4\)
- \(1 \leq a_i \leq 10^9\)
Output
Output contains one line, the minimum total price of the extension cords Procat needs to buy. You don't need to output a newline at the end of the output.