Description

Domo is a brilliant dog. One day, he accidentally gets trapped in a maze with multiple floors. Let's find the shortest path for him to escape!
This maze is cube-like, with each block, except the barricade blocks, containing an integer that represents the time required to pass through it.
When you want to exit this maze, the time you spend will be the sum of integers on your path from the start to the exit, including the starting block and the exit block.
You can move only right, forward, and down from every position. However, please note that you cannot move into a barricade block or move out of the cube.
i.e.: If you are at pos[i][j][k], you can move to three positions (only when it's inside the cube and not a barricade):
- pos[i+1][j][k]
- pos[i][j+1][k]
- pos[i][j][k+1]
If the size of this cube is N * M * K, the exit is always at position maze[N-1][M-1][K-1], and you always start from maze[0][0][0].
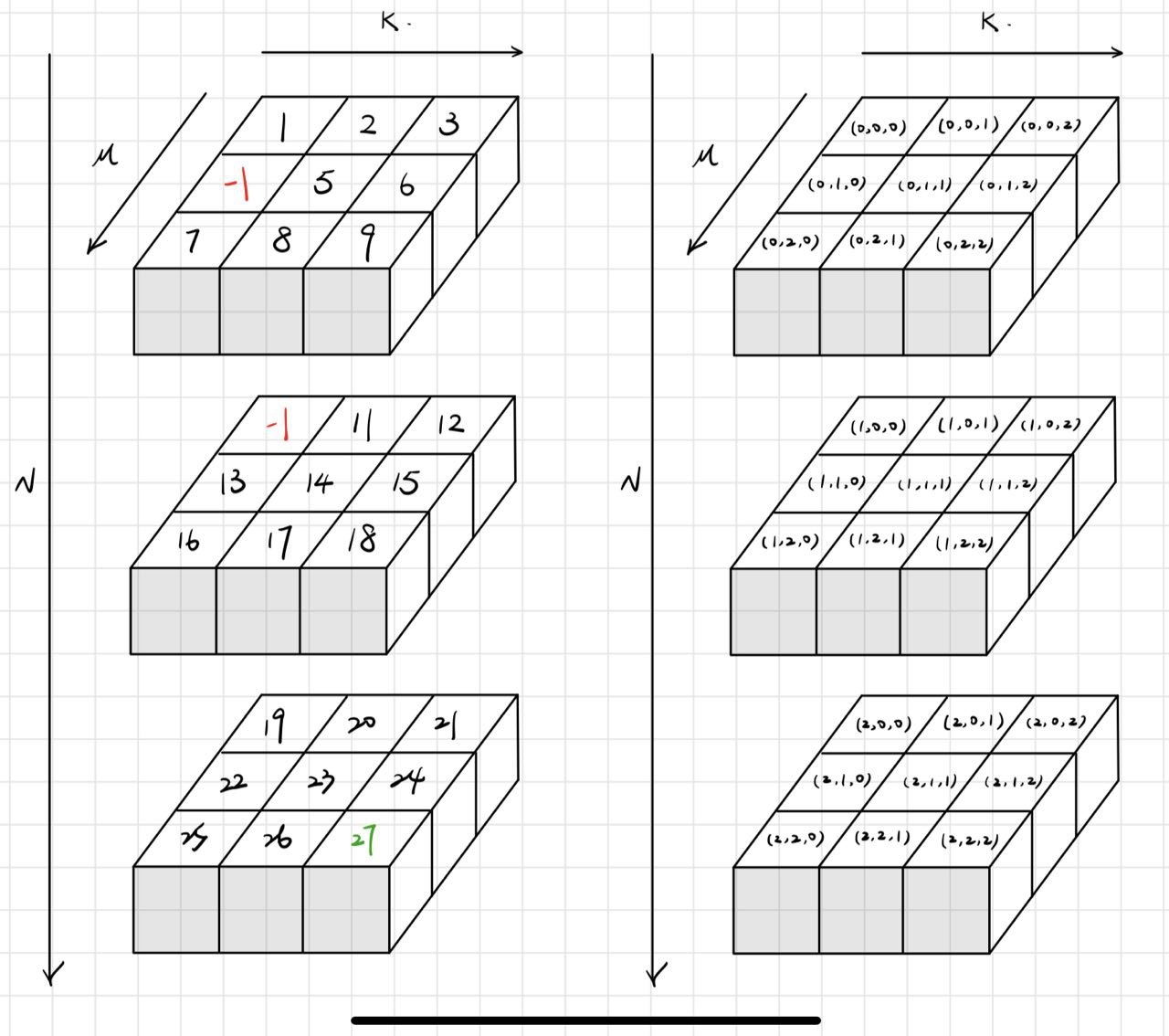
For example, in a 3 * 3 * 3 maze, with the cost of each block and barricades shown below, the shortest path to the exit would be [1, 2, 3, 6, 9, 18, 27], and the cost would be 66.
In this picture, the left side indicates the time you spend on the block, and the right side indicates the index of each block.
Input
The first line consists of three integers N, M, K (1 ≤ N, M, K ≤ 100), describing the size of the maze. The number of floors is N, and each floor is M * K.
For the next N * M lines, each line contains K integers A1, A2, ..., Ak, describing the layout of the maze. (1 ≤ Ai ≤ 100 or Ai is -1)
If Ai is -1, it indicates that the block is a barricade, and you cannot enter that block.
Lines 2 through M+1 describe the layout of the first floor,
lines M+2 through 2M+1 describe the layout of the second floor,
and so on.
Output
Output the minimum cost of the time you spend to exit this maze. Remember to print a newline character at the end of the line.