Description

Just before the deadline for Doraemon to submit his final project to the eeclass system, another power outage occurred, causing him to lose all of his homework files. It seems that fate has determined that Doraemon will have to retake the course next year...

Fortunately, the government is making efforts to assist Doraemon's university in addressing this power issue by establishing a new electrical substation! The electrical grid for the campus consists of n-1 cables connecting each of the n locations, ensuring that any two locations can be connected.

Previously, we established a substation (in problem 14080 - Power Outage), but power outages have occurred again... It appears that the strategies to balance the number of locations haven't proven effective. However, we have discovered that minimizing the distance from each location to the substation can efficiently reduce energy loss and significantly decrease the chance of encountering another power outage issue.

To determine the optimal location for its construction, they need to find the location where the greatest distance from the station to any other location is minimized.

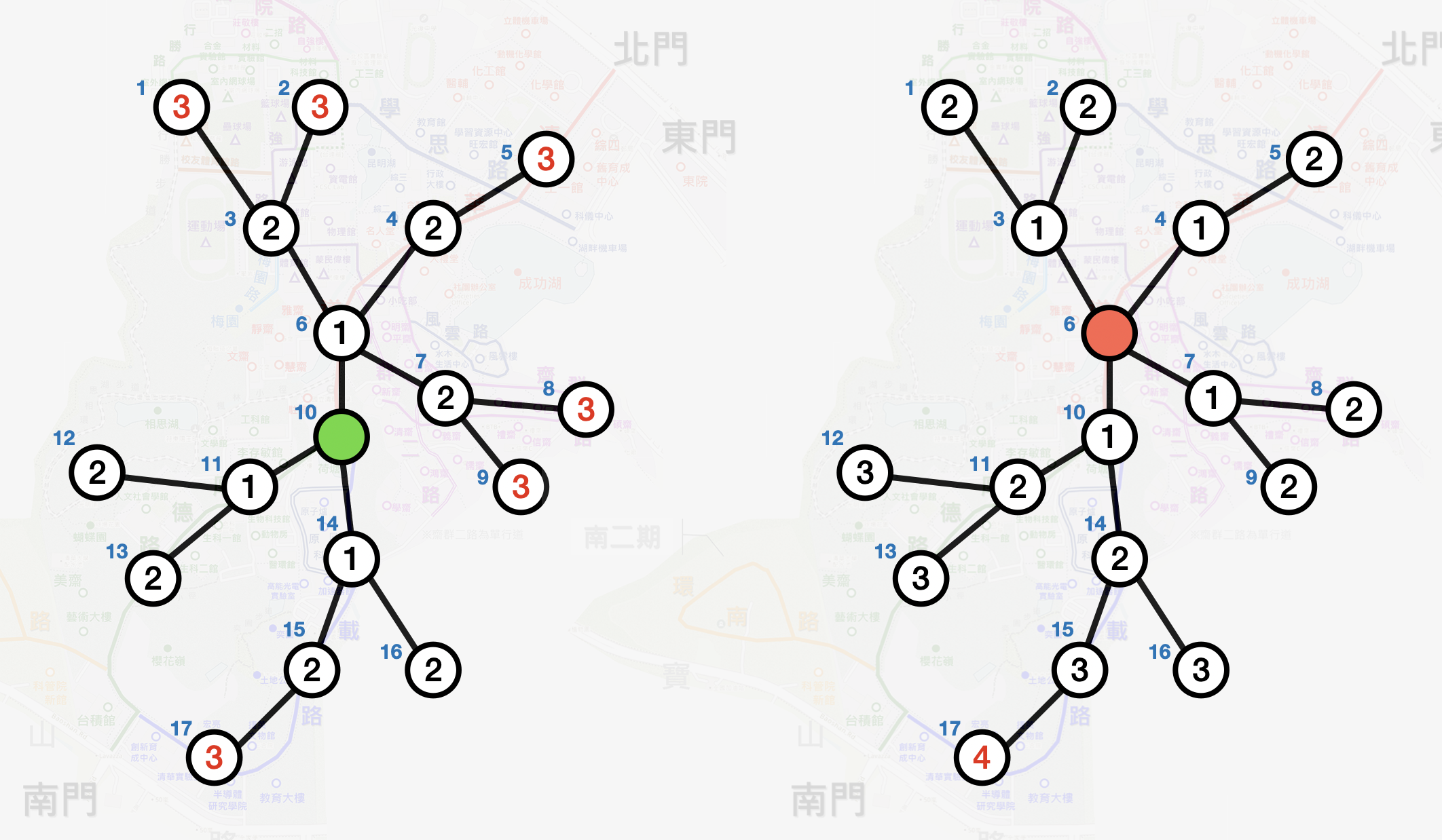
The graph above represents the layout of the electrical grid for the campus. Each circle represents a location, and each line connecting the locations represents a power cable with a distance of 1 unit. The blue numbers beside the circles indicate the index number of location, and the value inside each circle represents the distance from the electrical substation.

If we establish the substation at location index number 10 (in green), the farthest distance from there would be 3 units.
However, if we establish the substation at location index number 6 (in red), the farthest distance from there would be 4 units.
Therefore, it seems that establishing the electrical substation at location index number 10 might be the best choice.

Template

#include <stdio.h>
#include <stdlib.h>
#define N 100001

int cable[N][2], neighborCount[N], *neighbor[N];
int n;

void readGraph() {
    scanf("%d", &n);
    for (int i=0; i<n-1; i++) {
        scanf("%d %d", &cable[i][0], &cable[i][1]);
        neighborCount[cable[i][0]]++;
        neighborCount[cable[i][1]]++;
    }
    for (int i=1; i<=n; i++) {
        neighbor[i] = (int*)malloc(neighborCount[i] * sizeof(int));
    }
    int neighborIndex[N] = {};
    for (int i=0; i<n-1; i++) {
        int u = cable[i][0], v = cable[i][1];
        neighbor[u][neighborIndex[u]++] = v;
        neighbor[v][neighborIndex[v]++] = u;
    }
}

int main() {
    readGraph();
    // Test the following code
    /*
    for (int i=1; i<=n; i++) {
        int neighborCnt = neighborCount[i];
        printf("%d connects to ", i);
        for (int j=0; j<neighborCnt; j++) {
            printf("%d ", neighbor[i][j]);
        }
        printf("\n");
    }
     */
    return 0;
}

Utilizing the provided readGraph() function can help in managing the preprocess of the given graph:

• neighborCount[i] stores the number of neighbors for the i-th location.
• neighbor[i] is a dynamic array with a size equal to neighborCount[i], and it stores the index number of neighbors for the i-th location.

Try uncommenting the code in the main() function to see how it works.

Constraints

• Testcase 1~6 - n ≤ 10³
  • 1: he provided electrical grid is arranged in a straight line. (a₁ <--> a₂ <--> a₃ <--> ... <--> a_n)
  • 2~3: For the optimal location of a substation, the sum of the number of locations for each cable direction yields the same value, and the farthest distance for each direction of cable is also the same.
  • 4~6: No additional constraints.
• Testcase 7 (Bonus) - n ≤ 10⁵
  • ​No additional constraints. (hint: consider to conduct multiple tree searches and record additional information)

Input

The first line contain one positive integer n (1 ≤ n ≤ 10⁵) - the number of locations in the electrical grid.
Each of the following n-1 lines contains two integers u and v (1 ≤ u, v ≤ n) - a power cable connecting location index numbers u and v. It is guaranteed that the provided graph is a tree.

Output

Output one line contain one integer - the number of the location that is the best choice for establishing the electrical substation.

In this problem, there may be multiple locations considered optimal;
you should output the one with the smallest index number.

Sample Input  Download

Sample Output  Download

Tags

Discuss