Description

Just before the deadline for Doraemon to submit his final project to the eeclass system, another power outage occurred, causing him to lose all of his homework files. It seems that fate has determined that Doraemon will have to retake the course next year...

Fortunately, the government is making efforts to assist Doraemon's university in addressing this power issue by establishing a new electrical substation! The electrical grid for the campus consists of n-1 cables connecting all of the n locations, ensuring that any two locations can be connected. (This structure is also known as a tree, you can refer to the link for more detail.) 

The campus will be divided into different areas based on the location of the electrical substation after its construction. To maintain a balanced distribution of locations in each area and ensure a stable power supply, the goal is to identify the optimal location for the electrical substation where the maximum number of locations in each area is minimized.

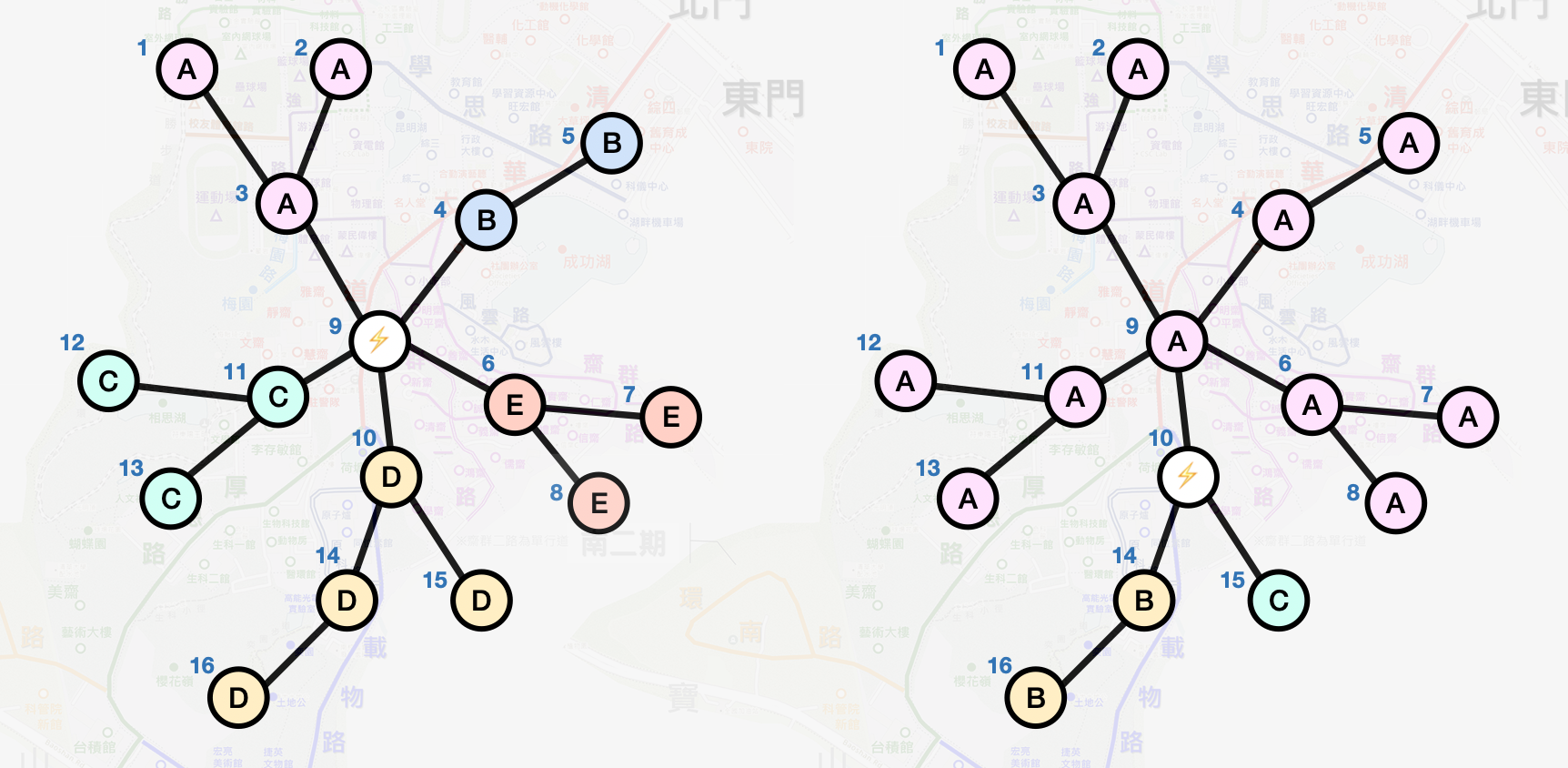
The graph above represents the layout of the electrical grid for the campus. Each circle represents a location, and each line connecting the locations represents a power cable with a distance of 1 unit. The blue numbers next to the circles indicate the index number of each location, and the English letter inside each circle represents the area split by the substation.

If we establish the substation at location index number 9 (left graph), we have:
Area A: 3 locations, Area B: 2 locations, Area C: 3 locations, Area D: 4 locations, Area E: 3 locations => max(3, 2, 3, 4, 3) = 4

If we establish the substation at location index number 10 (right graph), we have:
Area A: 12 locations, Area B: 2 locations, Area C: 1 location => max(12, 2, 1) = 12

Therefore, it seems that establishing the electrical substation at location No. 9 might be better than location No. 10.

Template

#include <stdio.h>
#include <stdlib.h>
#define N 100001

int cable[N][2], neighborCount[N], *neighbor[N];
int n;

void readGraph() {
    scanf("%d", &n);
    for (int i=0; i<n-1; i++) {
        scanf("%d %d", &cable[i][0], &cable[i][1]);
        neighborCount[cable[i][0]]++;
        neighborCount[cable[i][1]]++;
    }
    for (int i=1; i<=n; i++) {
        neighbor[i] = (int*)malloc(neighborCount[i] * sizeof(int));
    }
    int neighborIndex[N] = {};
    for (int i=0; i<n-1; i++) {
        int u = cable[i][0], v = cable[i][1];
        neighbor[u][neighborIndex[u]++] = v;
        neighbor[v][neighborIndex[v]++] = u;
    }
}

int main() {
    readGraph();
    // Test the following code
    /*
    for (int i=1; i<=n; i++) {
        int neighborCnt = neighborCount[i];
        printf("%d connects to ", i);
        for (int j=0; j<neighborCnt; j++) {
            printf("%d ", neighbor[i][j]);
        }
        printf("\n");
    }
     */
    return 0;
}

Utilizing the provided readGraph() function can help in managing the preprocess of the given graph:

• neighborCount[i] stores the number of neighbors for the i-th location.
• neighbor[i] is a dynamic array with a size equal to neighborCount[i], and it stores the index number of neighbors for the i-th location.

Try uncommenting the code in the main() function to see how it works.

Input

The first line contain one positive integer n (1 ≤ n ≤ 10⁵) - the number of locations in the electrical grid.
Each of the following n-1 lines contains two integers u and v (1 ≤ u, v ≤ n) - a power cable connecting location index numbers u and v. It is guaranteed that the provided graph is a tree.

Output

Output one line contain one integer - the number of the location that is the best choice for establishing the electrical substation.
It's guaranteed that there is only one optimal location.

Sample Input  Download

Sample Output  Download

Tags

Discuss