Description
In the previous problem, you helped Stiff Waist Beast implement a basic convolutional layer. However, in the real use of CNN, there are more variations of convolutional layers such as stride and padding, and more additional steps including rotation and max pooling. Stiff Waist Beast now wants you to implement these features for him.
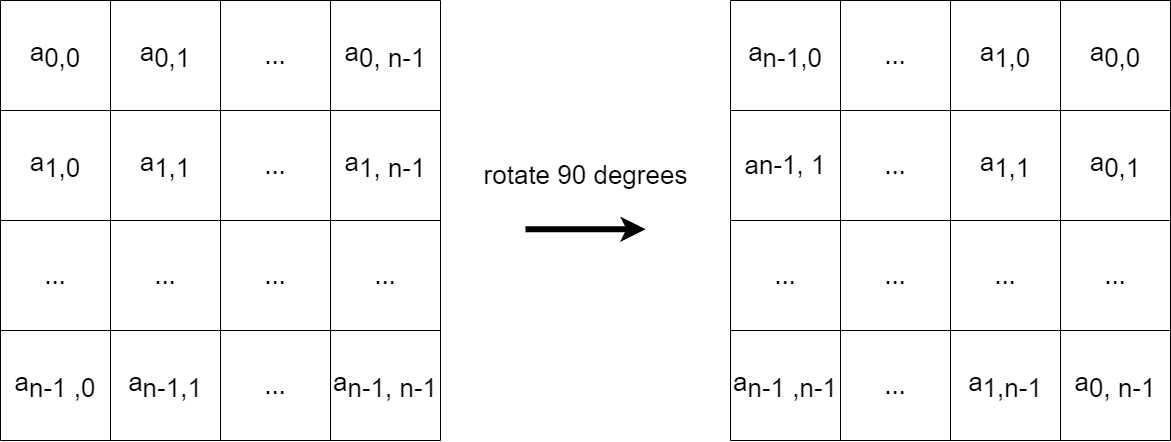
In this problem, given an n * n image and an m * m filter, you need to rotate it 90 degrees clockwise for r times first, then apply the convolution with two parameters p and s, and finally do the max pooling with k * k's square.
- Step 1: Rotate the image with 90 degrees clockwise for r times
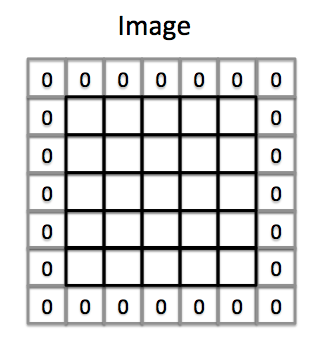
- Step 2: Padding
In a complete convolution layer, padding is a commonly used operation. The definition of padding is to add p rows and p columns extra zeros around the edges of the image before convolution, so that we can control the size of output.
- Step 3: Strided Convolution
Besides, the stride defines how many pixels the filter shifts at each iteration of convolution. Note that for an iteration where the filter exceeds the boundary of the image, the iteration should be skipped.

The complete convolution is defined as follows:
Given an n * n image A and an m * m filter B, we will first pad A to the size of (n+2p)*(n+2p) and notate it as Apad, and then do the convolution while shifting the filter with s pixels. The resulting feature map after convolution is another matrix C, where each element of C is computed as
The size of matrix C is thus ceil((n + 2*p - m + 1) / s) * ceil((n + 2*p - m + 1) / s), where ceil(.) returns the smallest integer value which is greater than or equal to the specified number and the term ceil((n + 2*p - m + 1) / s) can be calculated as follows:
int conv_size = (n+2*p-m+1)/s;
if((n+2*p-m+1)%s != 0) conv_size++; - Step 4: Max Pooling
After convolution, we need to use max pooling to help reduce data size, which is defined as follows:
After convolution, in every k * k square of the feature map C, we will choose the maximum value. If the length of some boundary part is less than k, you can still pick the maximum value of that part.
Explanation of the sample input:
After rotation:
21 16 11 6 1
22 17 12 7 2
23 18 13 8 3
24 19 14 9 4
25 20 15 10 5
After padding:
0 0 0 0 0 0 0
0 21 16 11 6 1 0
0 22 17 12 7 2 0
0 23 18 13 8 3 0
0 24 19 14 9 4 0
0 25 20 15 10 5 0
0 0 0 0 0 0 0
After convolution with stride = 2:
42 6 -4
46 25 5
50 29 9
Note1:
Since the array is large, please declare it as a global variable:
int A[505][505];
int main(){
//your code
return 0;
}
Note2:
In max pooling, the maximum value can be negative. So remember to initialize the "maximum" variable to be an extremely small negative value.
Input
The first line is an integer T, denoting that there will be T testcases.
The first line of each testcase will have six integers: n, m, k, r, p, s.
Each of the following n lines has n integers, denoting image A.
Each of the following m lines has m integers, denoting filter B.
1 <= t <= 10, 1 <= n <= 500, 1 <= m, k <= min(n, 5), 0 <= r <= 1e5, 0 <= p <= m, 1 <= s <= m
In testcases 1, 2: r = 0, p = 0, s = 1
In testcases 3, 4: r > 0, p = 0, s = 1
In testcases 5, 6: r = 0, p > 0, s = 1
In testcases 7, 8: r = 0, p = 0, s > 1
In testcases 9, 10: no other restriction
Output
Print the 2D array after rotation, padding, strided convolution and max pooling.
Remember to print '\n' after each line, and a space after each number.