Description
What is a Binary Search Tree?
A binary search tree (BST) is a binary tree data structure with the following properties:
- Each node in the tree has at most two child nodes (binary tree).
- For any node, its value is greater than or equal to the values stored in the left subtree.
- For any node, its value is smaller than the values stored in the right subtree.
- For any node, the left subtree and the right subtree are binary search trees respectively as well.
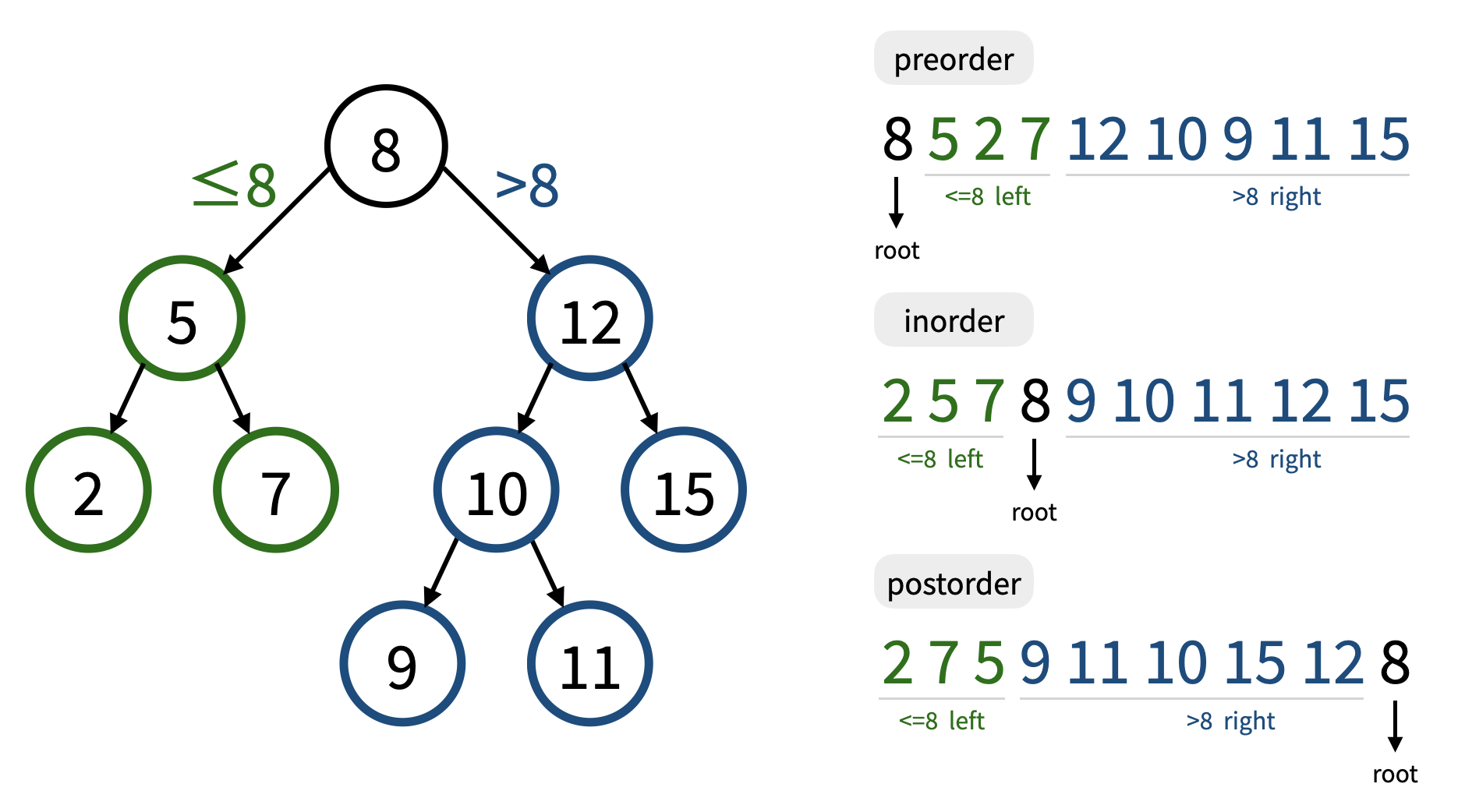
We know that the preorder traversal is based on the order "root -> left subtree -> right subtree". Therefore, for the preorder traversal sequence of a binary search tree, we can observe that the first number is the root of the tree, and in the following sequence, numbers smaller than or equal to the root belong to the left subtree (green part), while numbers larger than the root belong to the right subtree (blue part).
In this problem:
You are given the preorder and inorder sequences of a scrambled binary search tree with unique node values, where we would choose several internal nodes of the original tree and swap each of these nodes with its left or right child.
Please note that in this problem, we guarantee that every non-leaf node has two children, but we do not guarantee that the tree is a perfect binary tree. Besides, we guarantee that no two swapped pairs overlap (that is, contain a same node). In the following image, each color represents a node pair that has been swapped.
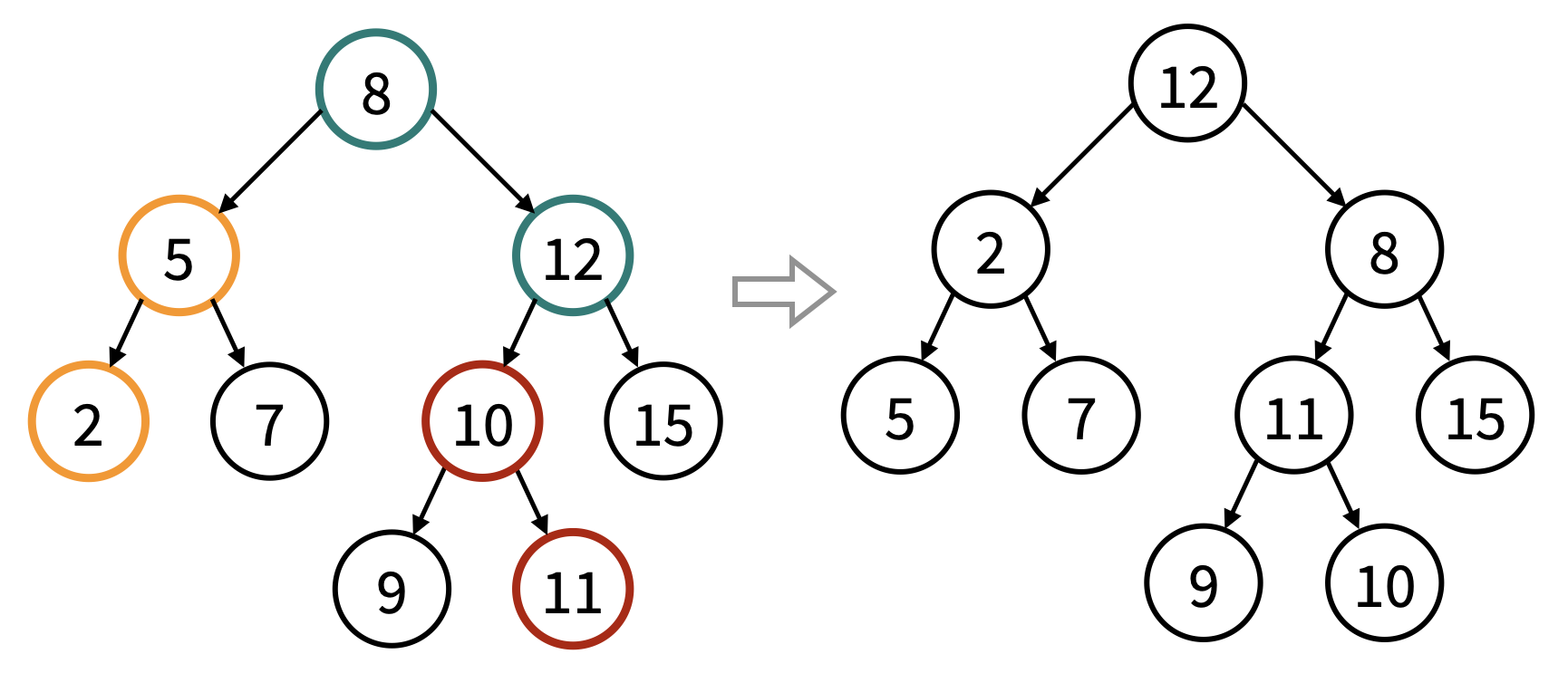
Can you help us reconstruct the original binary search tree and output its postorder sequence?
Input
- The first line contains an integer N (1 ≤ N ≤ 103) - the length of the preorder and the inorder sequences for the scrambled binary search tree.
- The second line contains N integers x1, x2, ..., xN (1 ≤ xi ≤ 105) - representing the preorder sequence.
- The third line contains N integers y1, y2, ..., yN (1 ≤ yi ≤ 105) - representing the inorder sequence.
Test case constraints
- Testcases 1-2: The given tree is a perfect binary tree (see the definition in 13846), and no swapping operations have been applied.
- Testcases 3-4: No swapping operations have been applied.
- Testcases 5-6: The given tree is a perfect binary tree, and for each operation, the chosen node can only be swapped with its left child.
- Testcases 7-8: For each operation, the chosen node can only be swapped with its left child.
- 如果同學已經通過前四筆,只要建樹的時候多檢查子樹的root和left child之間是否需要交換,並交換回來,即可通過第五到八筆。在陣列中,left child在root的下一位,只要一行判斷就好。
- Testcases 9-10: No further constraints.
Hints
- To pass Testcases 1-4, the tree construction method similar to that in 13846 can be applied based solely on the preorder sequence.
- To pass Testcases 5-8, the tree construction method similar to that in 13846 can be applied based solely on the preorder sequence. And, you know where the left child of the current subtree's root is located. See if they have been swapped.
- To pass Testcases 9-10, you should use both the preorder and the inorder sequences.
Output
Output one line that contains N integers - representing the postorder sequence of the original binary search tree. Remember to print '\n' at the end.