Description
What is a Perfect Binary Tree?
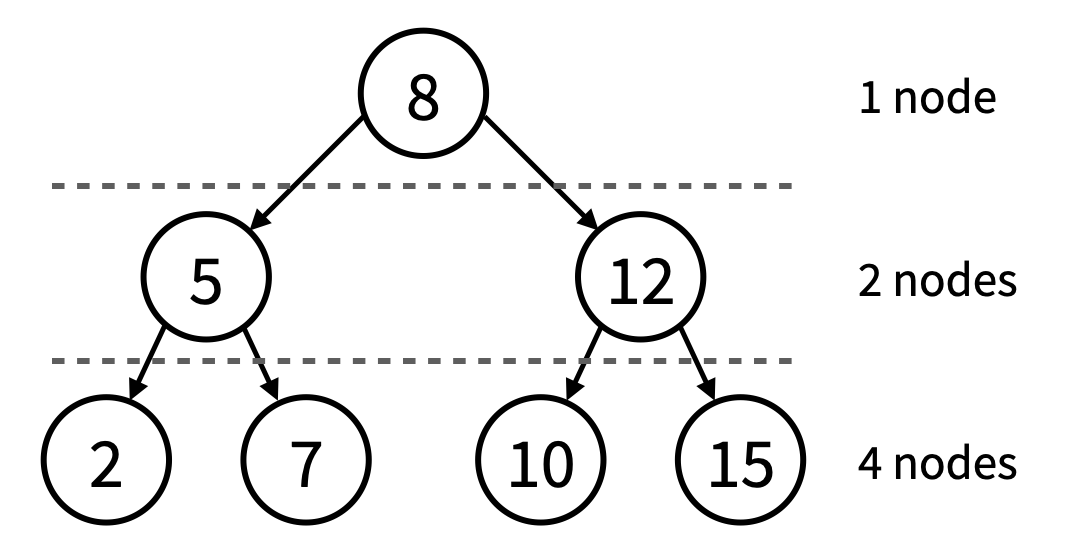
A perfect binary tree is a binary tree data structure with the following characteristics:
- Every level of the tree is completely filled with nodes. In other words, each level has the maximum number of nodes possible for that level.
- Each node in the tree has either two children or no children, and a node that has no children makes it a leaf node.
- The total number of nodes in a perfect binary tree of height h is 2h+1 - 1. (Note that the height of the following example tree is 2 not 3.)
What is a Binary Search Tree?
A binary search tree (BST) is a binary tree data structure with the following properties:
- Each node in the tree has at most two child nodes (binary tree).
- For any node, its value is greater than or equal to the values stored in the left subtree.
- For any node, its value is smaller than the values stored in the right subtree.
- For any node, the left subtree and the right subtree are binary search trees respectively as well.
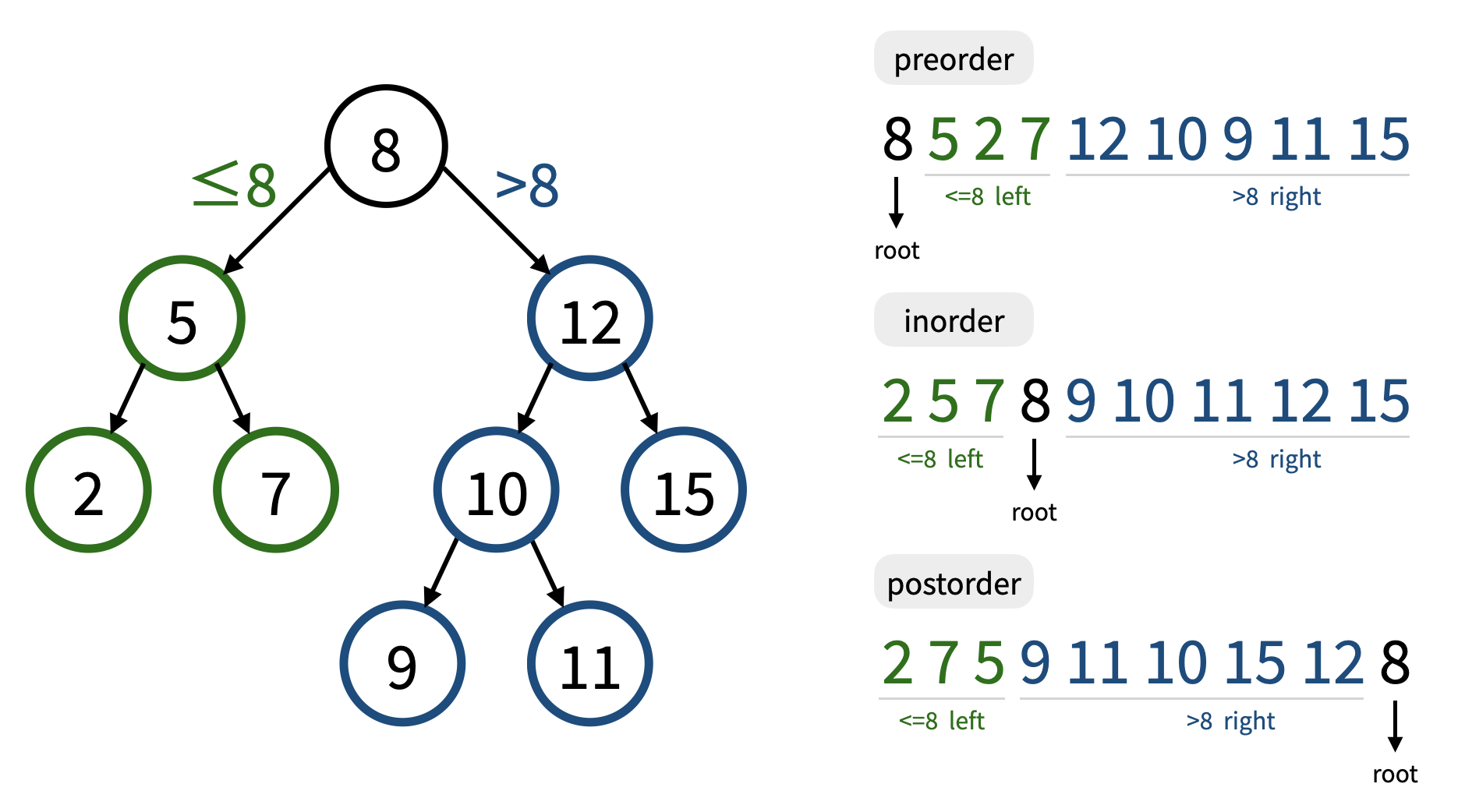
We know that the preorder traversal is based on the order "root -> left subtree -> right subtree". Therefore, for the preorder traversal sequence of a binary search tree, we can observe that the first number is the root of the tree, and in the following sequence, numbers smaller than or equal to the root belong to the left subtree (green part), while numbers larger than the root belong to the right subtree (blue part).
In this problem:
You are given the preorder sequence of a scrambled perfect binary search tree with unique node values, where the left and right subtrees of several nodes of the original tree have been swapped. See the following example of swapping node 8's and then node 12's left and right subtrees.
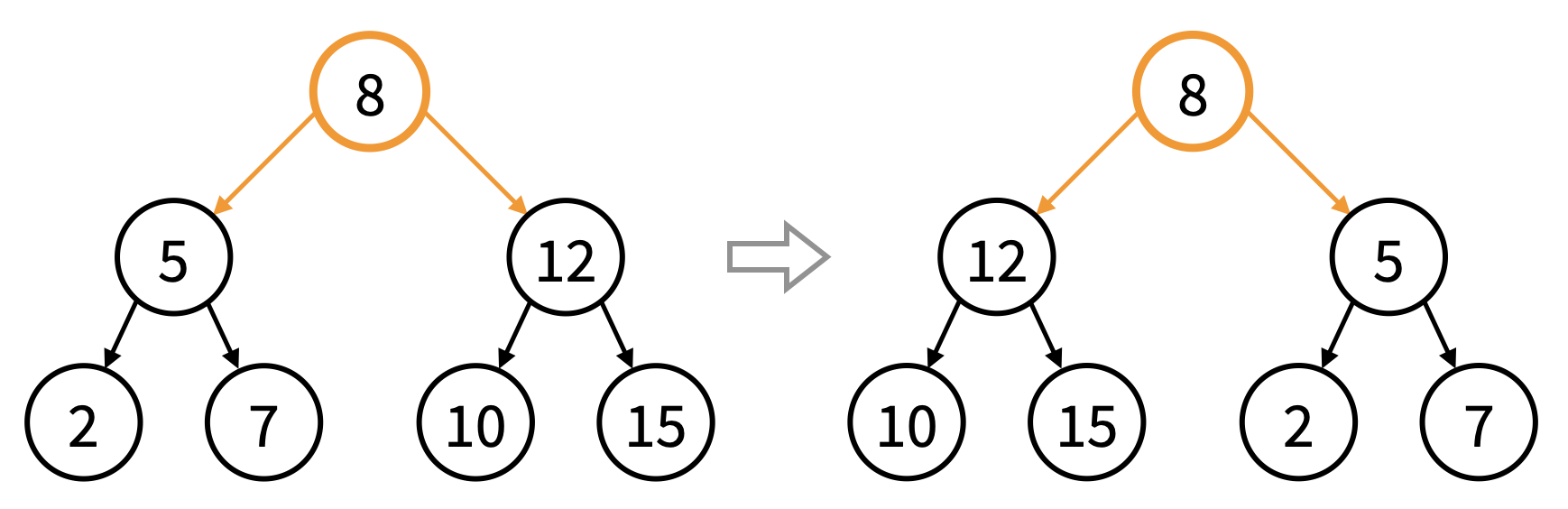
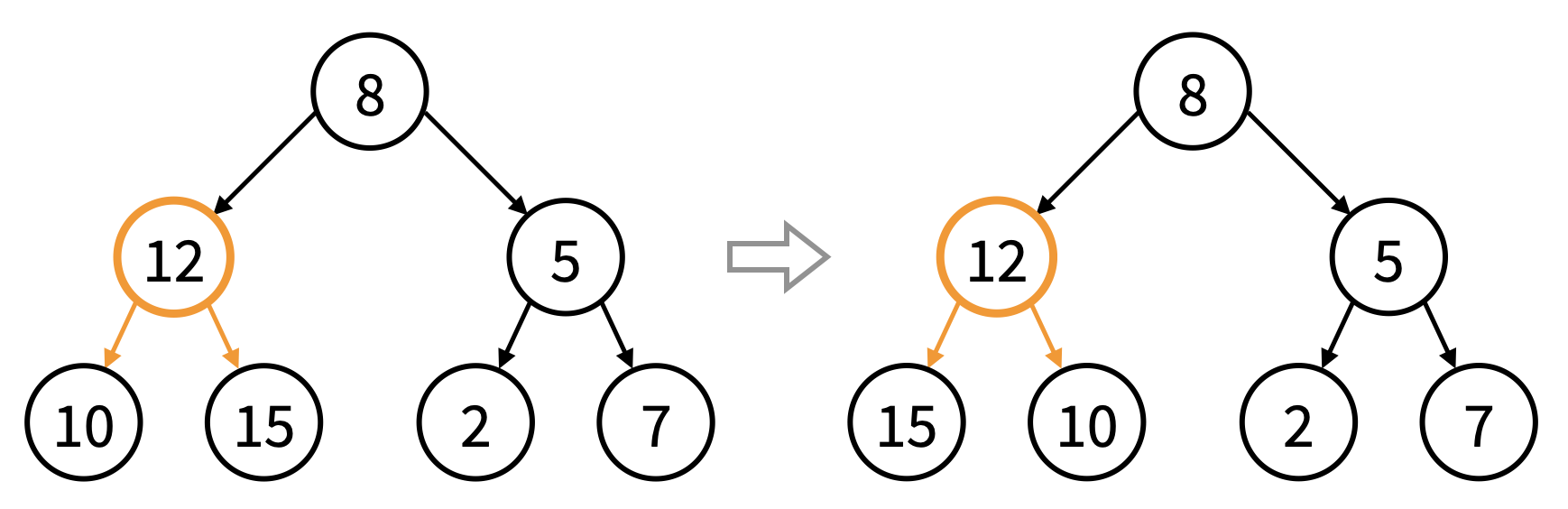
Can you help us reconstruct the original binary search tree and output its postorder sequence?
Input
- The first line contains an integer N (1 ≤ N ≤ 105) - the length of the preorder sequence for the scrambled perfect binary search tree.
- The second line contains N integers x1, x2, ..., xN (1 ≤ xi ≤ 109) - representing the preorder sequence.
Output
Output one line that contains N integers - representing the postorder sequence of the original perfect binary search tree. Remember to print '\n' at the end.