Description
Given several prefix expressions, each representing a function. Such an expression has at most 4 types of operations and 5 variables, described below.
We explain the 4 types of operations using infix:
- Addition. ‘a+b’ means a plus b, in which a, b are integers.
- Subtraction. ‘a-b’ means a minus b, in which a, b are integers.
- Multiplication. ‘a*b’ means a times b, in which a, b are integers.
- Function call. ‘f@a’ means return the value f(a), in which f is a function and a is an integer.
For variables, they are all integers, and the 5 variables are A, B, C, D, and X, respectively. For A, B, C, and D, you will get their values from input. For X, it is the parameter that you gave the function.
The function name will be a lowercase letter. Given the function name and the prefix expression of each function. Now here are q queries: given the function name and the parameter (i.e., X) for the function, and the values of A, B, C, and D, please output the calculation result.
For sample input 2, here are the syntax trees for the 2 functions.
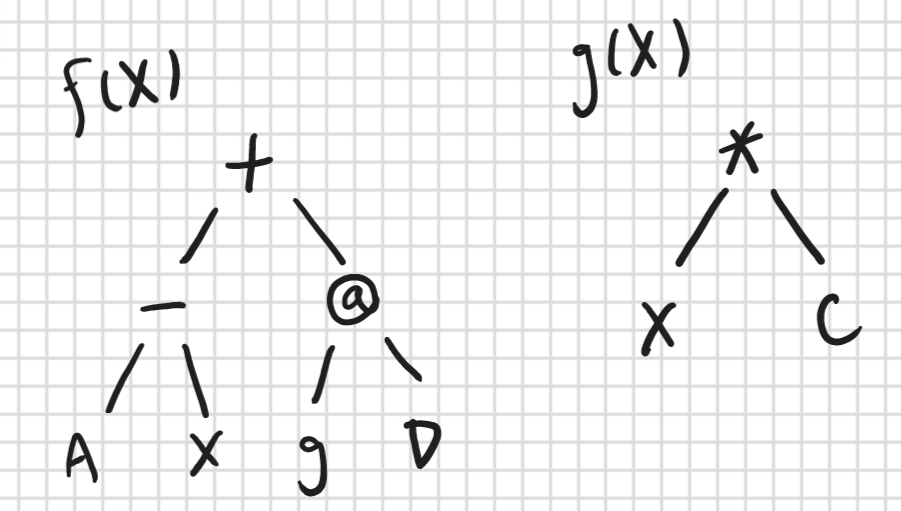
Note the parameter X for the functions are different. For example, in the second query, it’s 1 for f and it’s 5 for g.
Input
The first line contains two integers, n and q, which means there are n functions and q queries.
Each of the following n lines contains a lowercase letter representing the function name, and a string representing the prefix expression, separated by a space.
Each of the last q lines contains a lowercase letter and five integers, separated by spaces, representing the function name, the parameters X, A, B, C, and D, respectively.
Constraints:
1 ≤ n ≤ 26
1 ≤ q ≤ 100
-1000 ≤ A, B, C, D, X ≤ 1000
The expression would not contain over 200 characters.
For cases 1~3, the expressions only contain the first 3 operations.
For other cases, no further constraints.
Output
An integer that represents the calculation result. Since the answer could be large, please output the answer modulo 998244353. After modulo, the answer should be between 0 ~ 998244352.
Note
Since the answer should modulo 998244353, you should take the remainder after every operation (including returning the value of a single variable). Since the result of taking the remainder must be non-negative, the result should add 998244353 if it is negative after modulo. Be free to use the following function:
num %= 998244353;
if(num < 0) num += 998244353;
return num;
}