Description
In this problem, you have to implement a 2D convolution operation with zero-padding and stride.
Convolution is an operation that you elementwise multiply the sub-region in the original image(A larger 2D array) and the provided kernel(A smaller 2D array) and the summation of the multiplied values will be the new values in the output map(The size may be different from the original image). The multiplication follows a sliding window, so once we reach the bottom-right, we'll get a brand new 2D map.
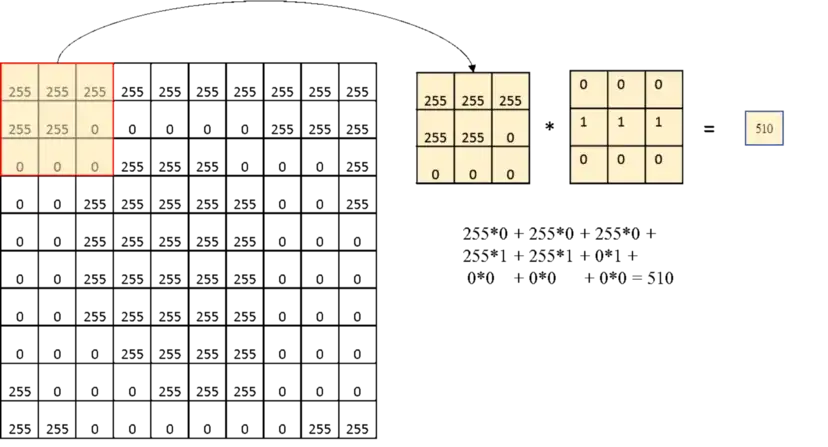
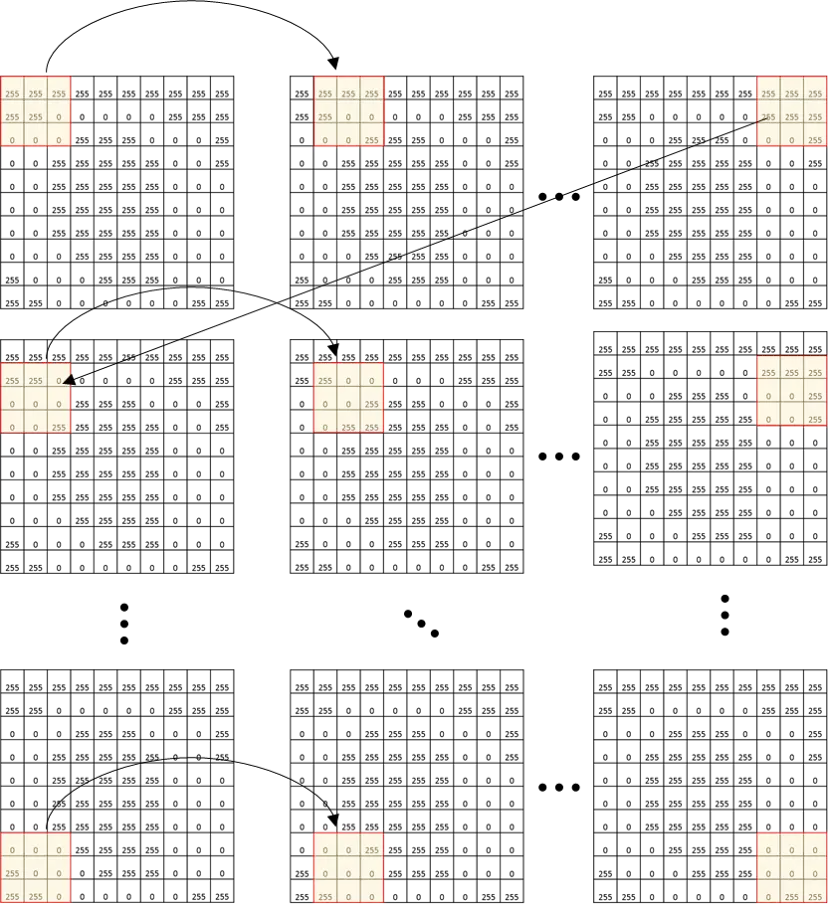
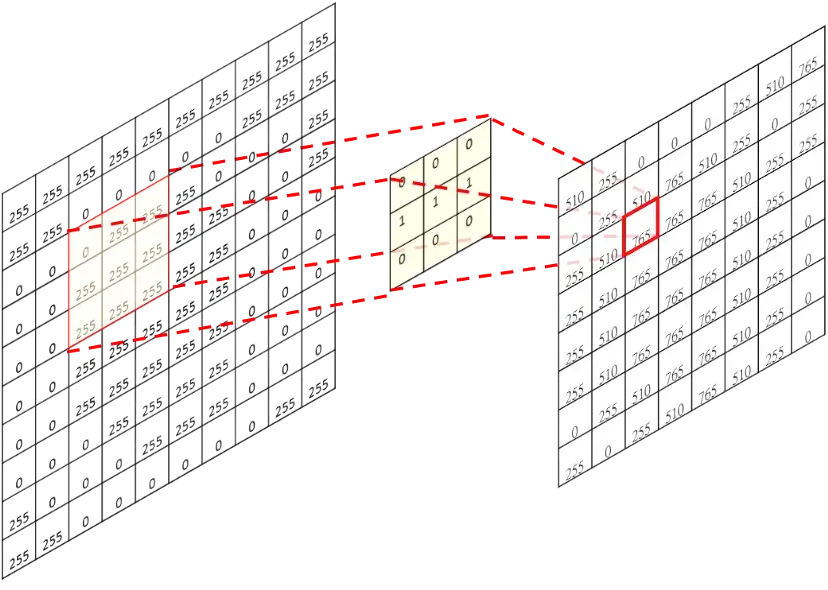
Once you understand how to do simple convolution, another trick in convolution is that you can pad the original map with zeros, which is called zero-padding.

Last, we can decide the step size of the sliding window, which is called stride.
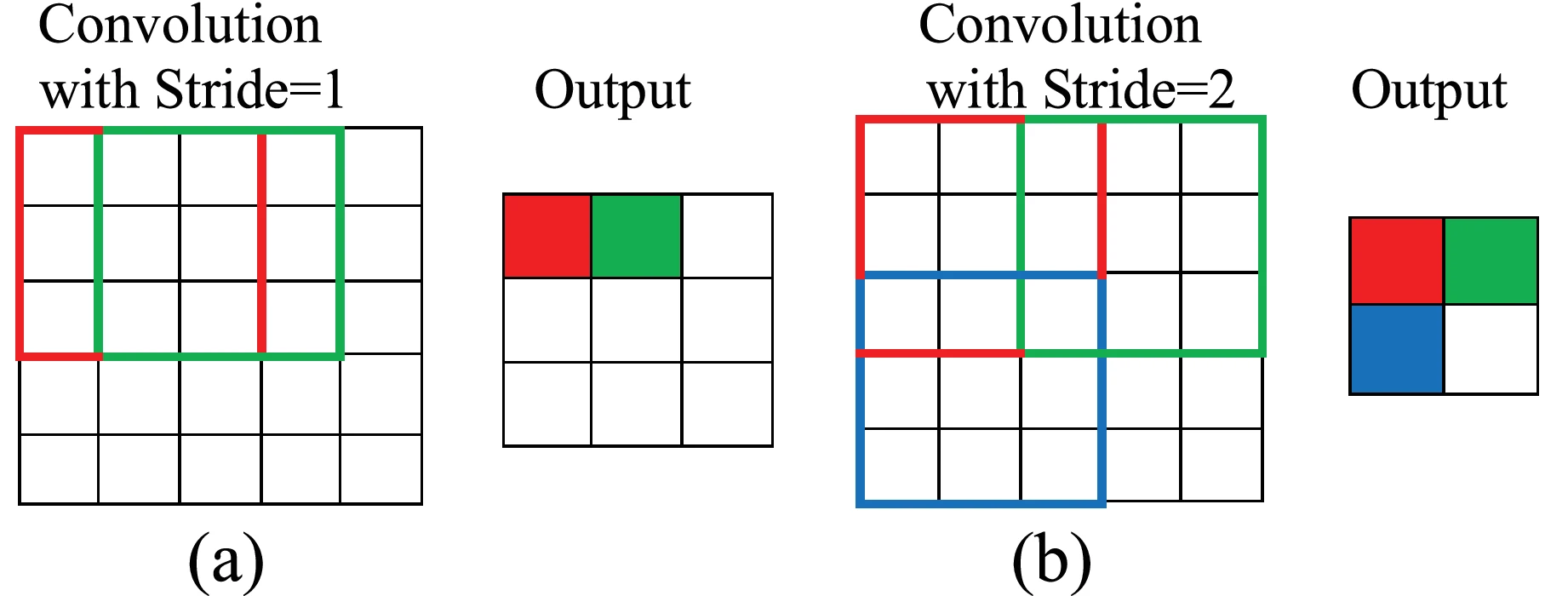
To sum up, you'll be given a 2D image and a 2D kernel, you are asked to do the convolution with the given padding size and stride.
Testcase 4: No padding, stride > 1 (Only considering stride)
Testcase 5: With padding, stride =1 (Only considering padding)
Testcase 6: With padding, stride > 1
Note that you only have to do the convolution in the valid region.
Input
The first line contains 2 integers, the height and the width of the 2D image, respectively. (1 <= height, width <= 1024)
Next, you have to read the whole 2D image.
The following line contains 2 integers, the height and the width of the 2D kernel, respectively. (1 <= height, width <= 10)
Then, you have to read the whole 2D kernel.
The last line will be the the size of stride and padding, respectively. (0 <= size of stride and padding <= 10)
All the values mentioned above are integers.
It is guaranteed every value of 2D images <= 255 and and 2D kernel is <= 10
Output
Please print the calculated 2D map.
The elements are separated by whitespace and you have to print '\n' at the end of each row.