Description
There is a tree consisting of n nodes, in which the root is numbered 1. The nodes are numbered 1, 2, …, n.
Each node has a lucky value v, and the range of the lucky value is in [1-10^9]. The lucky value is NOT distinct.
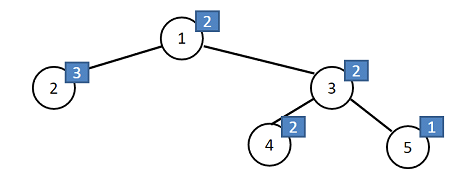
For example, below is a tree, where each number in the circle indicates the node ID, and the number in the blue square denotes the lucky value, e.g., node 1 has lucky value 2, and node 2 has lucky value 3.
For node 1, its subtree is the whole tree. All the distinct lucky values in node 1’s subtree are {1, 2, 3}.
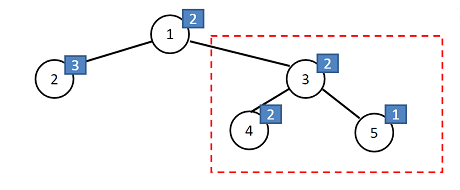
For node 3, its subtree contains nodes {3,4,5} (red dashed box below). All the distinct lucky values are {1, 2}.
We would like you to find out for each node i, the number of distinct lucky values in its subtree.
Input
Output
Print n integers: for integer i, print the number of distinct lucky values in node i's subtree. Every integer needs space behind it.
Please print '\n' at the end of output.