Description
Besides the shapes of tetrominoes and the width of the playing field, the basic description of this problem is the same as that of "13722 - Doraemon plays Tetris". (See the highlight of this part in red color.)

Doraemon's favorite video game is Tetris (俄羅斯方塊).
In Tetris, players complete lines by moving differently shaped pieces (tetrominoes), which descend onto the playing field. The completed lines disappear and grant the player points, and the player can proceed to fill the vacated spaces. The game ends when the uncleared lines reach the top of the playing field. - Wikipedia
You may refer to the gif for more detail demonstrating this game.
In this problem, we want to simulate the gaming process of Tetris, and several rules differ from the original Tetris:
- The playing field width is 4, and we have only 3 types of tetromino shapes.
- When the tetrominoes form a horizontal line, the line won't be disappeared but remains in the same place.
- You can only rotate the tetrominoes before you drop them into the field; you must decide the directions of the tetrominoes first and choose the place you want to put them in. The tetromino would fall until it touches the ground or the other tetrominoes.
The following figure shows the 3 types of tetrominoes. Please notice that their shape differs from "13722 - Doraemon plays Tetris".
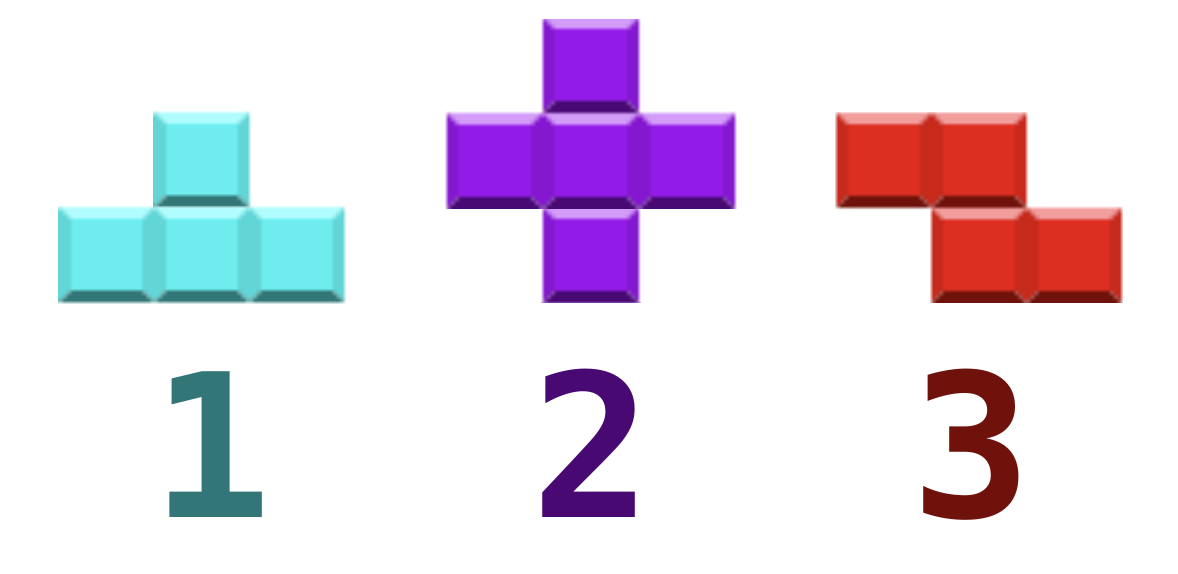
Given a sequence of the tetromino type, you must put it into the playing field by order.
If we put a tetromino into the field that the height of the stacked tetromino would exceed the top of the playing field, then the game would fail. In this problem, you only need to determine whether the game will end successfully; we can put all the tetrominoes into the field, and no tetromino exceeds the top of the playing field. (Notice: exactly reaching the top is acceptable in this problem)
If the game failed in the end, tell the game would end at x-th tetromino. Since we want to maximize the possible game time, please output the largest x.
******In this problem, please also notice the following part.
Since Doraemon keeps losing this game, he decides to use his gadgets (道具) to cheat on this! Symbols of two types of gadgets would appear in the sequence of the tetrominoes, representing the moment he can use them. You don't need to use them if you believe better strategies exist. If you choose to use a given gadget, you can only use it at the moment it occurs in the sequence, and the gadget can not be stored and used in the future.
Type 1: Air Cannon

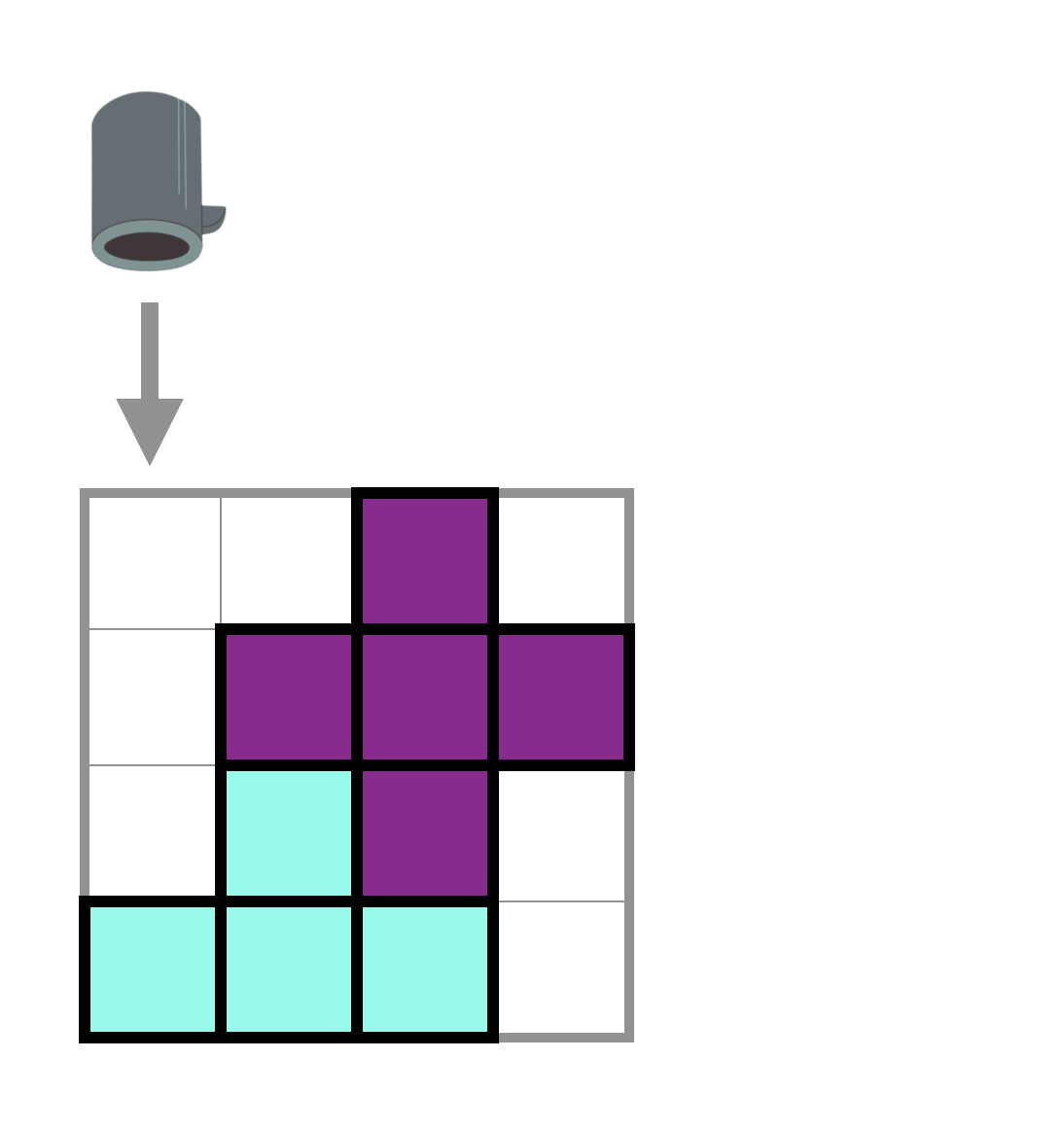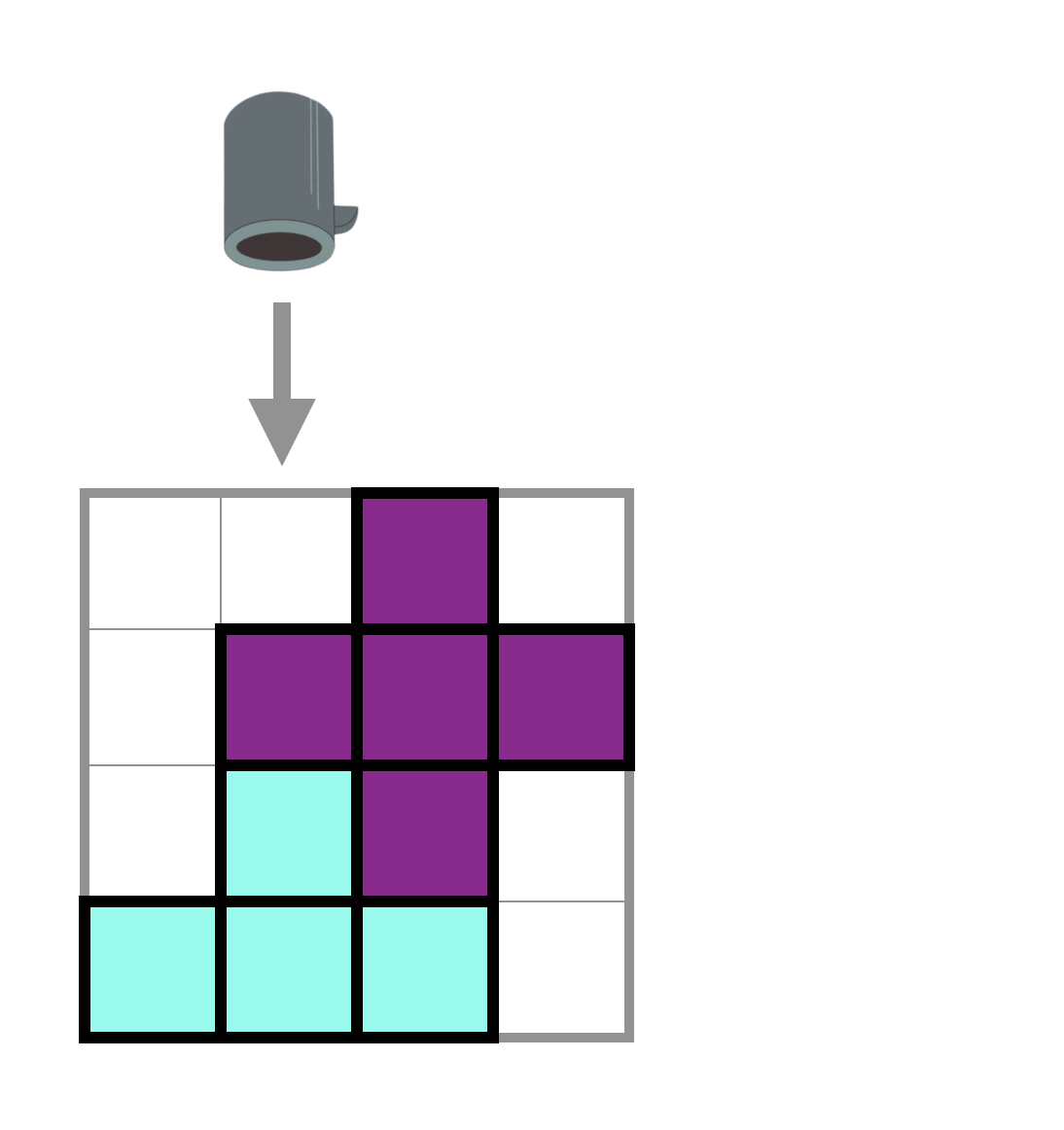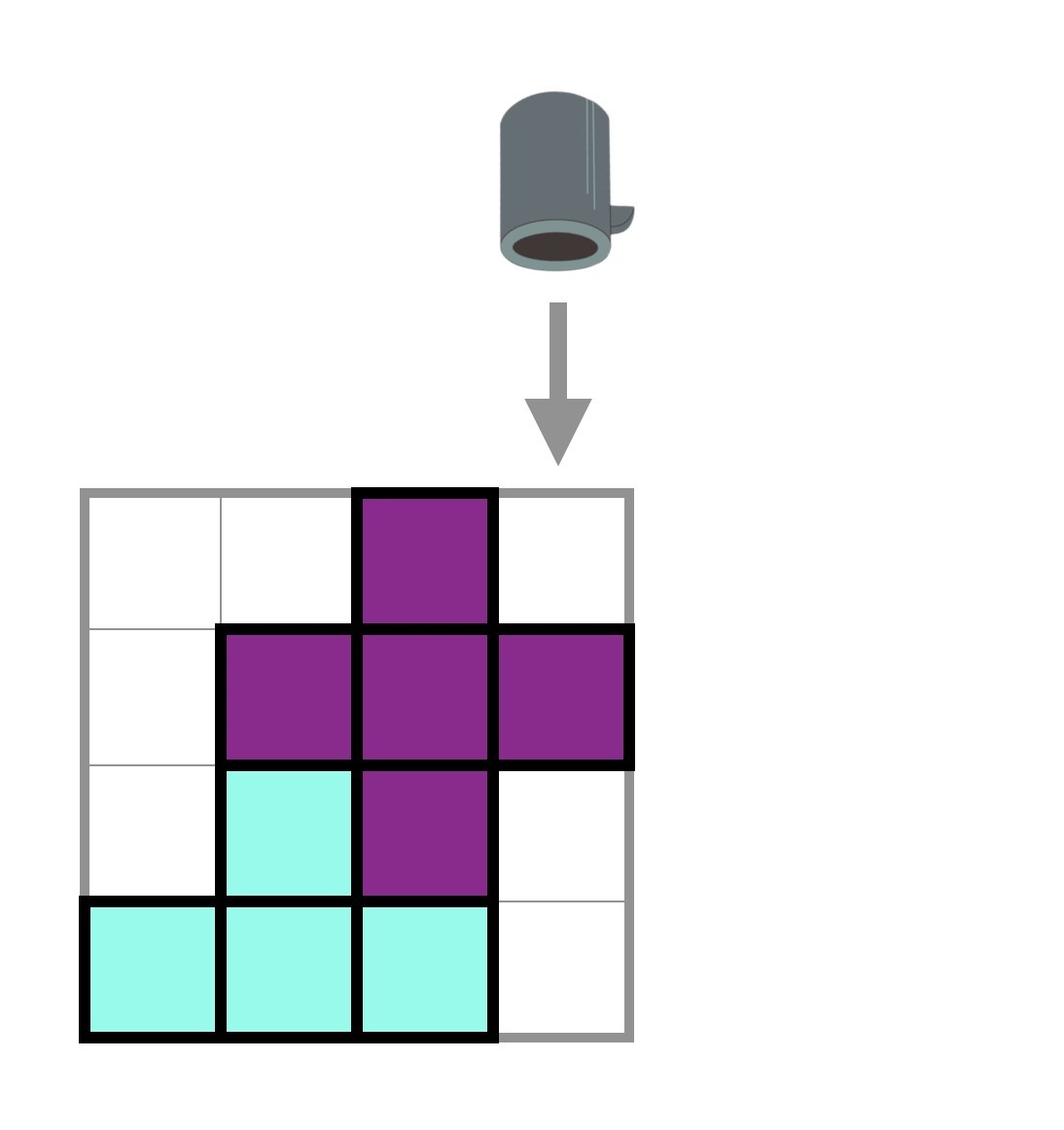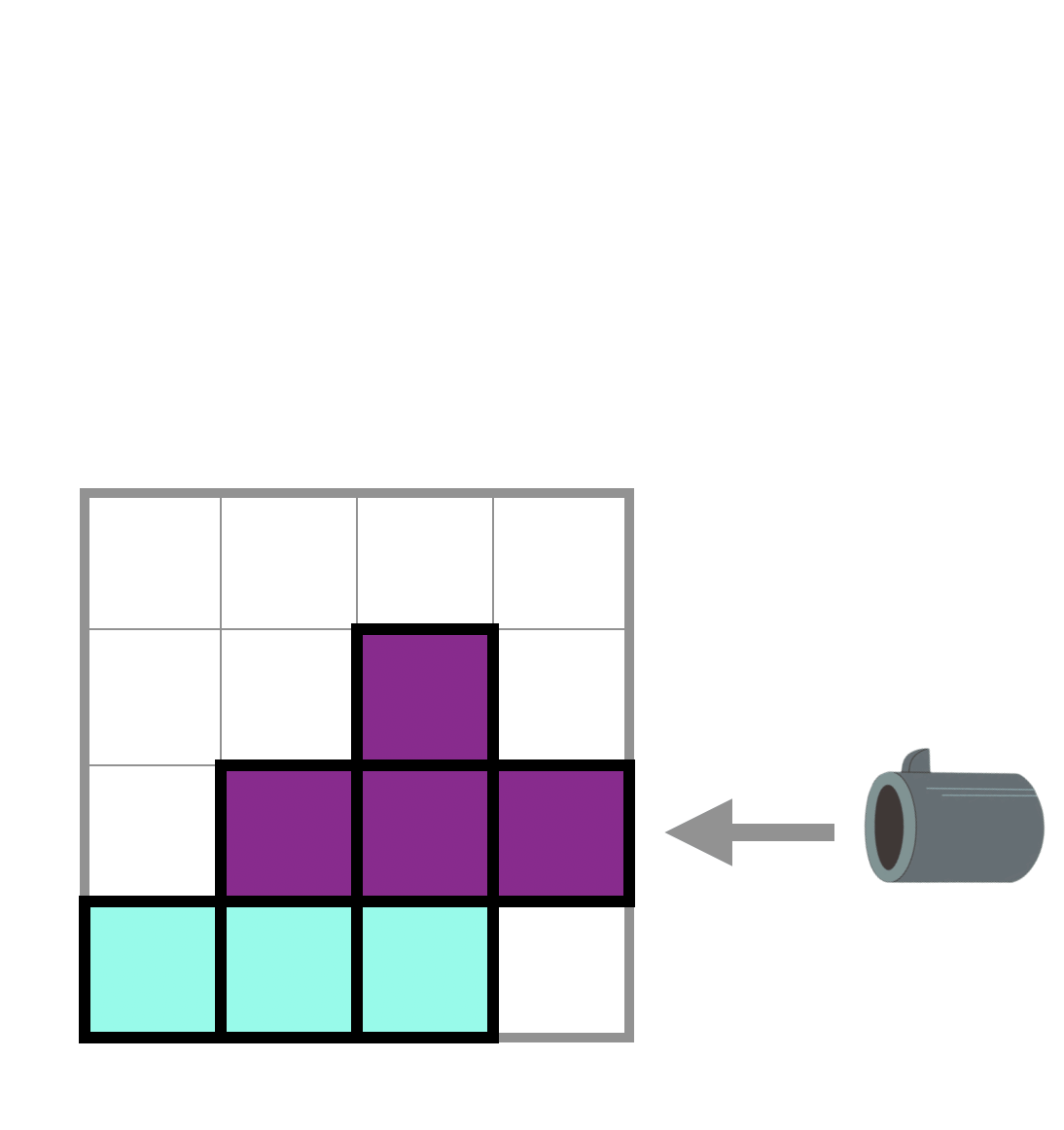
Using this type of gadgets, you can remove a specific row or column of the playing field. If you choose to remove a row of the playing field, all the remaining pieces above will descend by one block. We use -1 to represent this type of gadgets in the given sequence.
Type 2: Invisible Cape

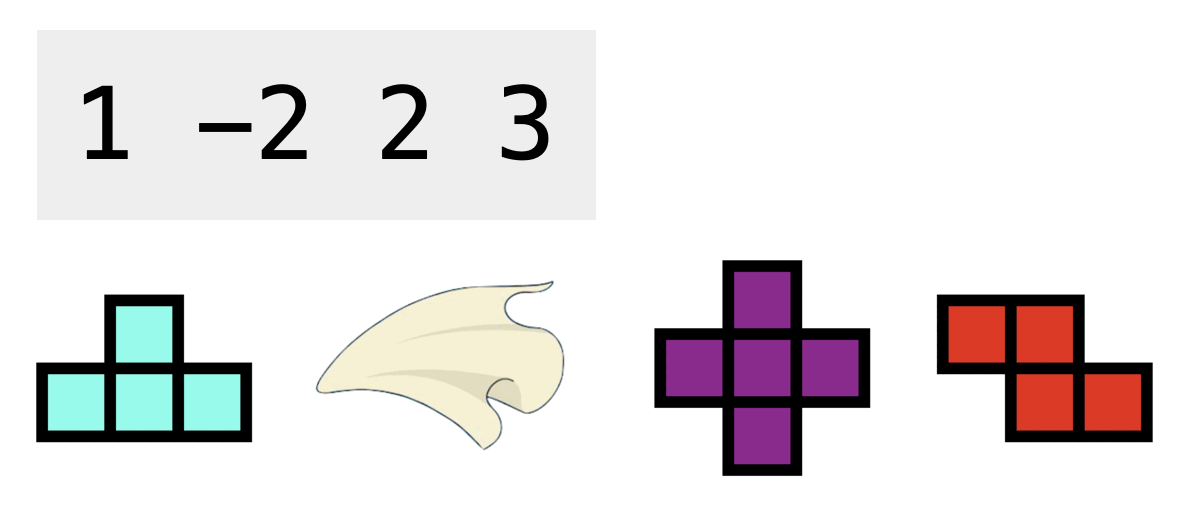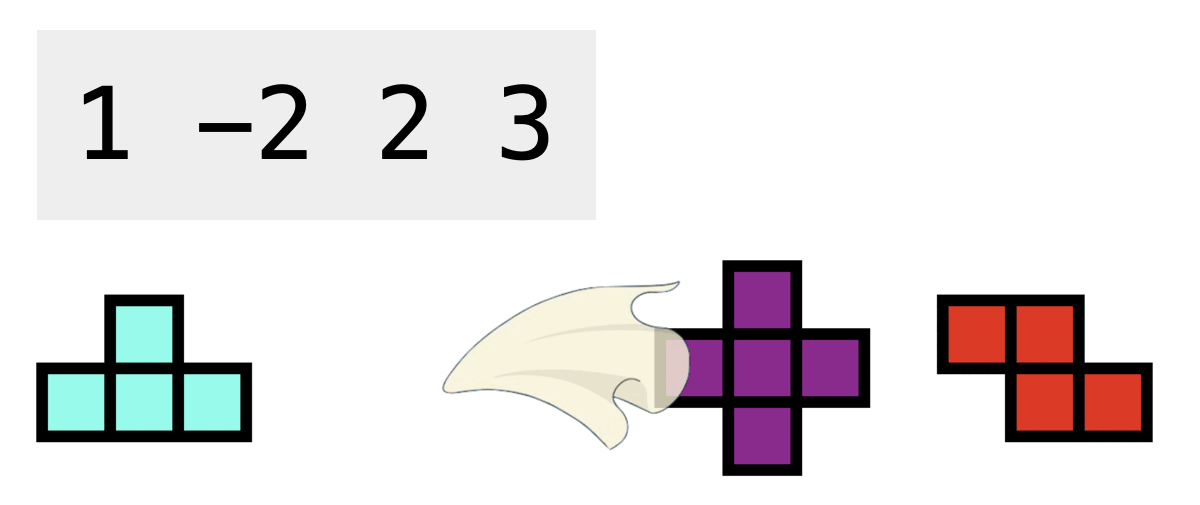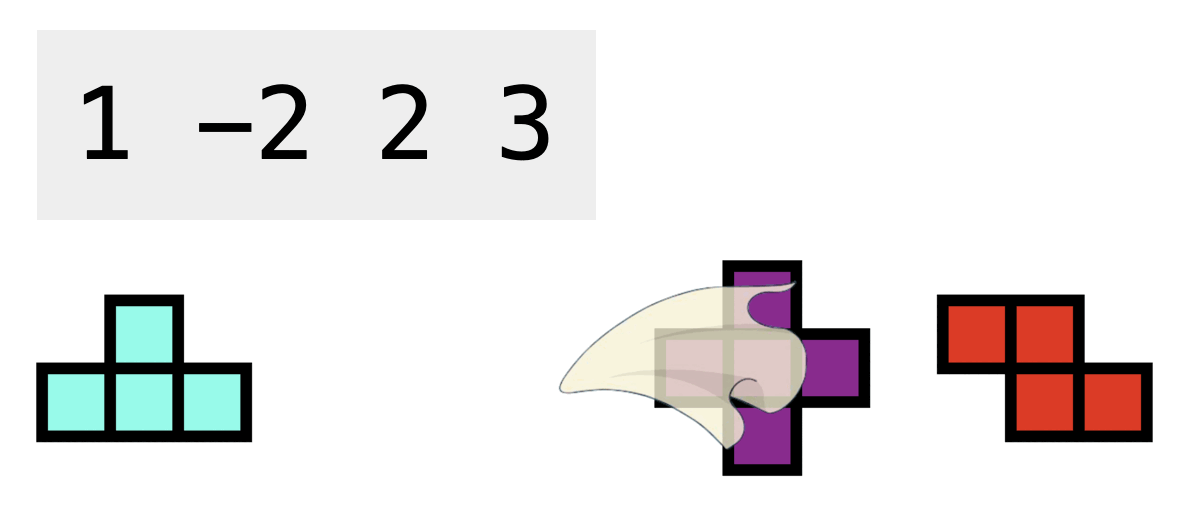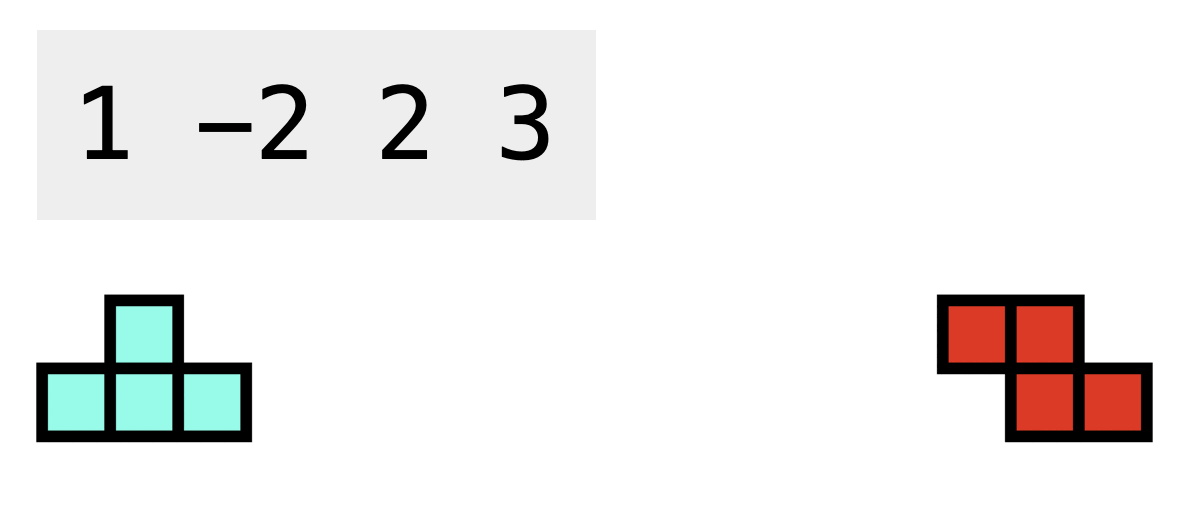
Using this type of gadgets, you can ignore the next upcoming tetromino, and we guarantee that it always comes before a tetromino in the sequence. This type of gadgets can only apply to the tetromino immediately after it. We use -2 to represent this type of gadgets in the given sequence.
You may refer to the following test case 2 demonstration to learn more about the operation of the gadgets.
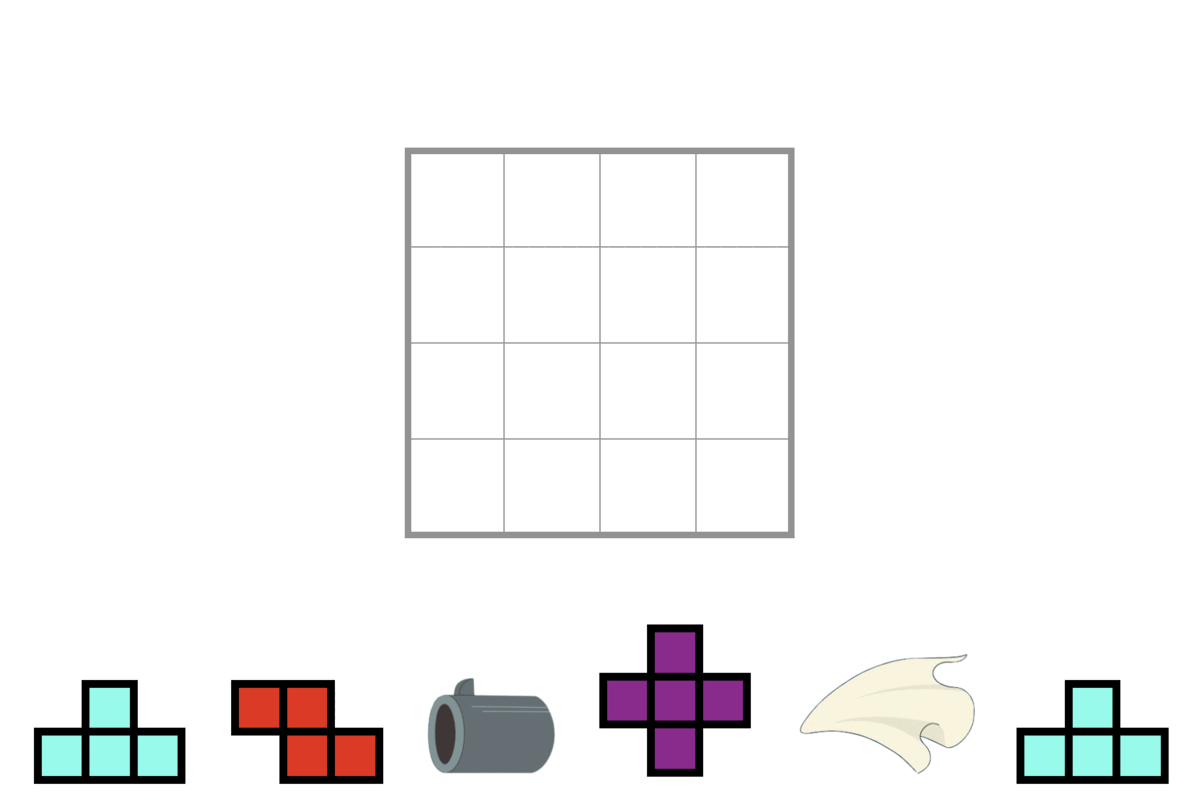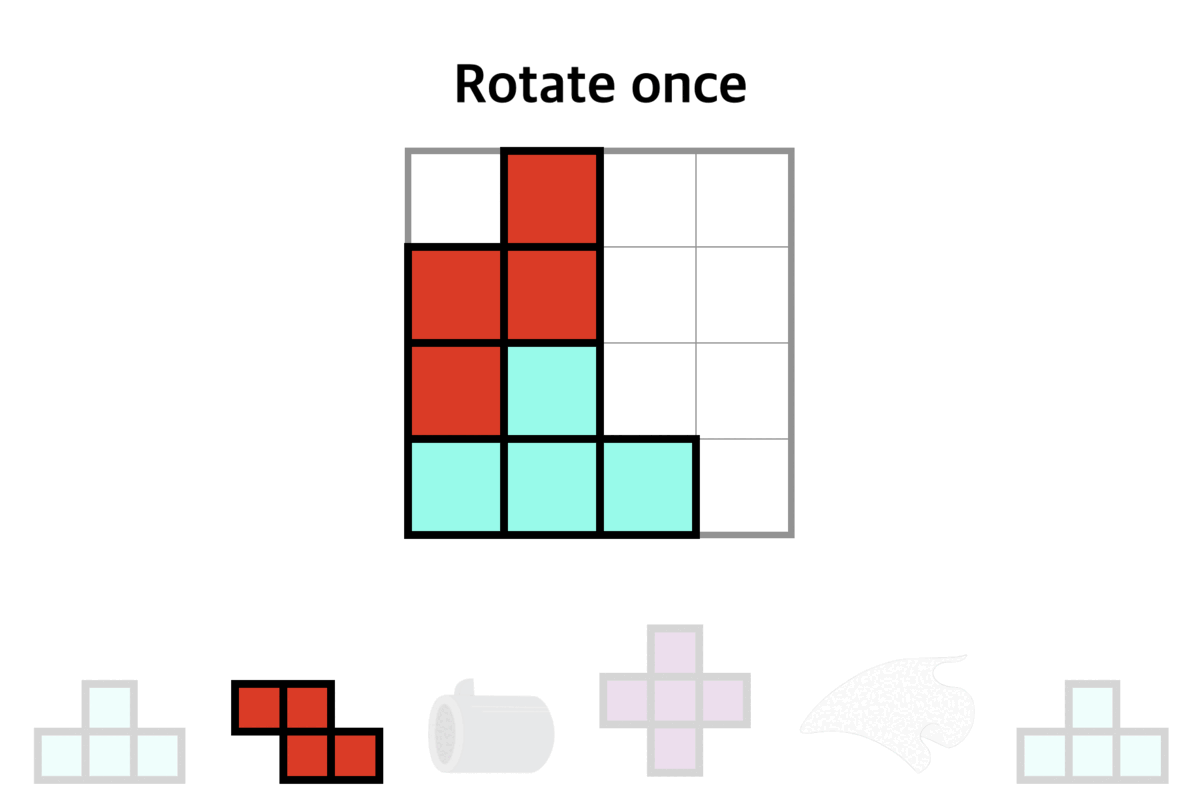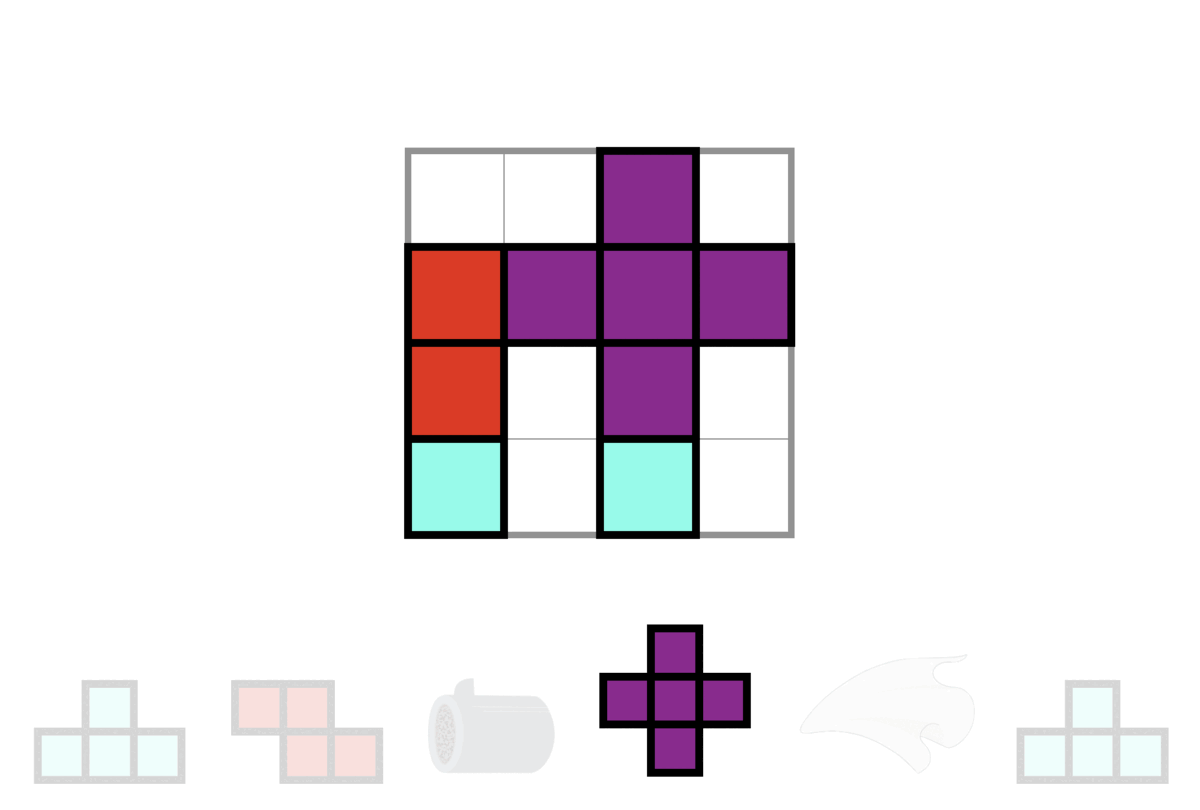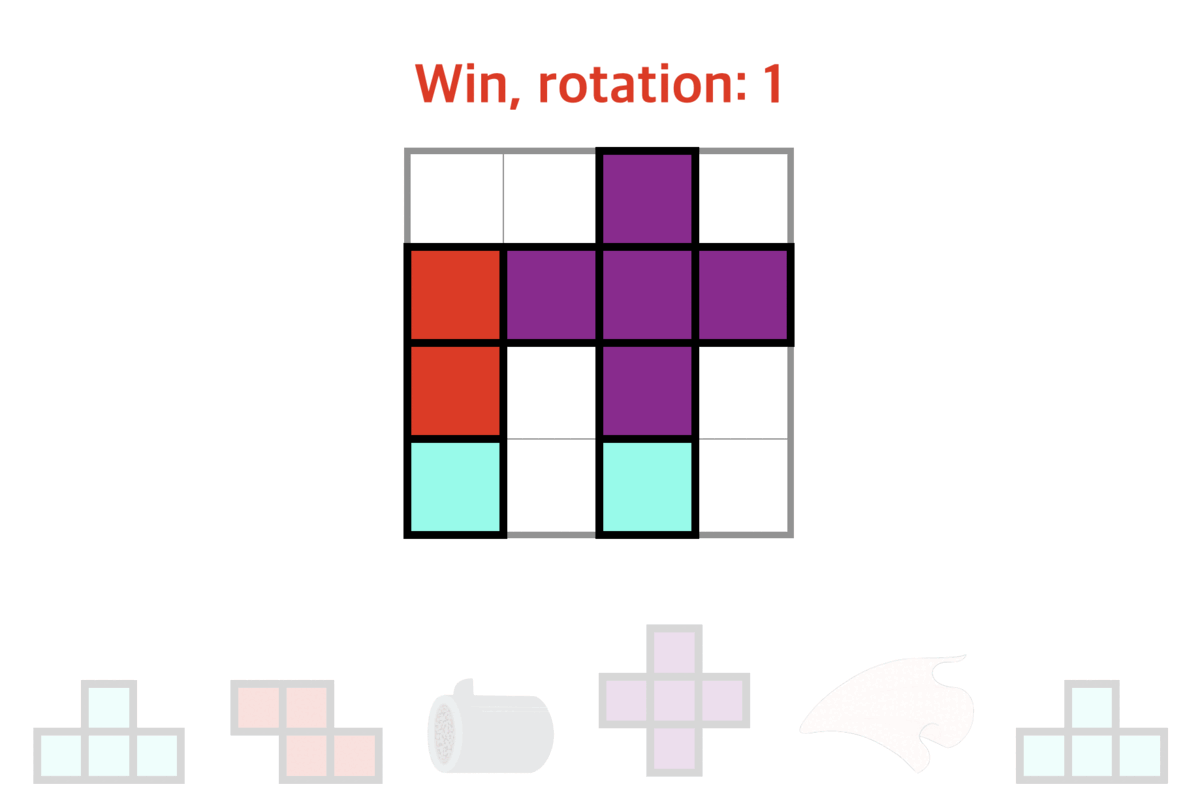
Since Doraemon is extremely lazy, he wants to minimize the number of "clockwise rotations" of tetrominoes. If he can win the game, please tell him the minimum times of clockwise rotations that are required.
So, in this problem:
- If Doraemon can win this game, calculate the minimum number of clockwise rotations.
- Otherwise, calculate the largest x that Doraemon would lose at the x-th term of the sequence. We can observe that the x-th term of the sequence must be a tetromino.
Test case constraints
Since Doraemon still needs to improve at this...
- 1~5: We guarantee that there won't have any gadgets in the sequence, and Doraemon will always lose
- 6~8: We guarantee that if Doraemon can win, the minimum number of times for the rotation must be 0
- 9~10: No further constraints in these test cases
Input
The first line contains a positive integer T ≦ 10, representing the number of test cases.
For each test case:
The first line contains two positive integers N, H ≦ 20, representing the tetrominoes' sequence length and the playing field's height. The second line contains N integers, which can be 1, 2, 3, -1 or -2, representing the type of each tetromino or gadget.
Output
For each test case, output one line.
- If Doraemon can win the game with a minimum of x times of clockwise rotations, print "Win, rotation: x\n".
- Otherwise, the game would end at the x-th term of the sequence, and you should print "Lose at x\n".