Description
In this homework, we are given a permutation P, where a permutation is an array consisting of n different integers from 1 to n. For example, [2,3,4,5,1] is a permutation, but [1,2,2] is not (2 occurs twice), and [1,3,4] is also not a permutation (n=3, but there is 4 in the array)
Assume there are n leaves in a full binary tree, from left to right. In each leaf, there is a number (called leaf number). Each leaf number is in the range [1,n], and the n leaf numbers form a permutation.
You could perform “operations” in the tree’s nodes. In a single operation, you can choose any non-leaf node in the tree and swap its left and right childs (along with their subtrees). For example, assume you have the tree below.
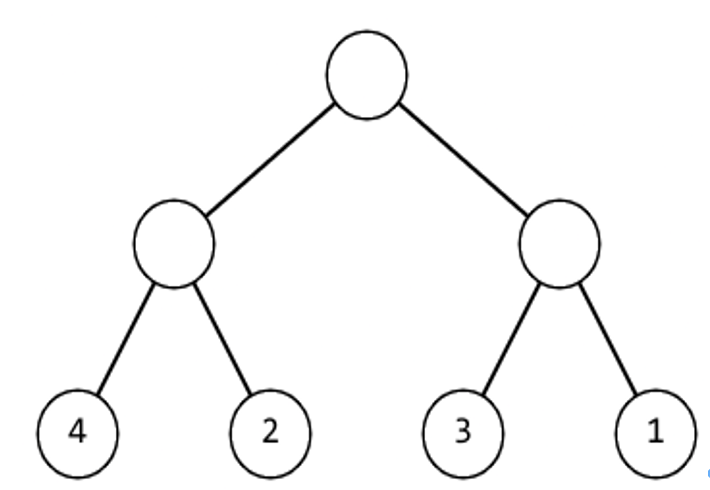
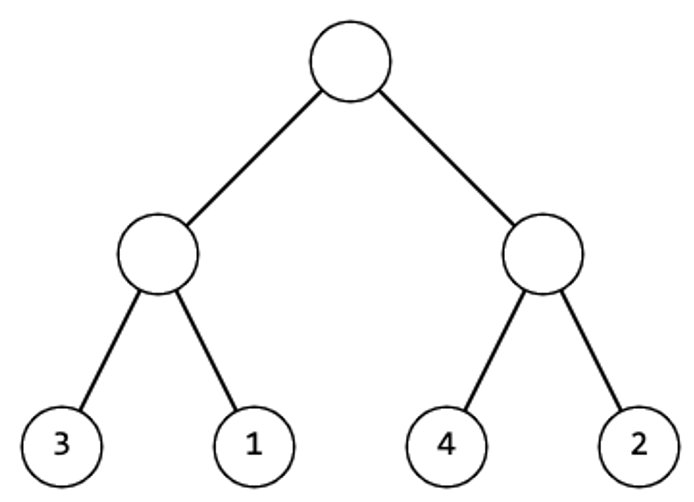
If you perform an operation to the root of the tree, the tree would become
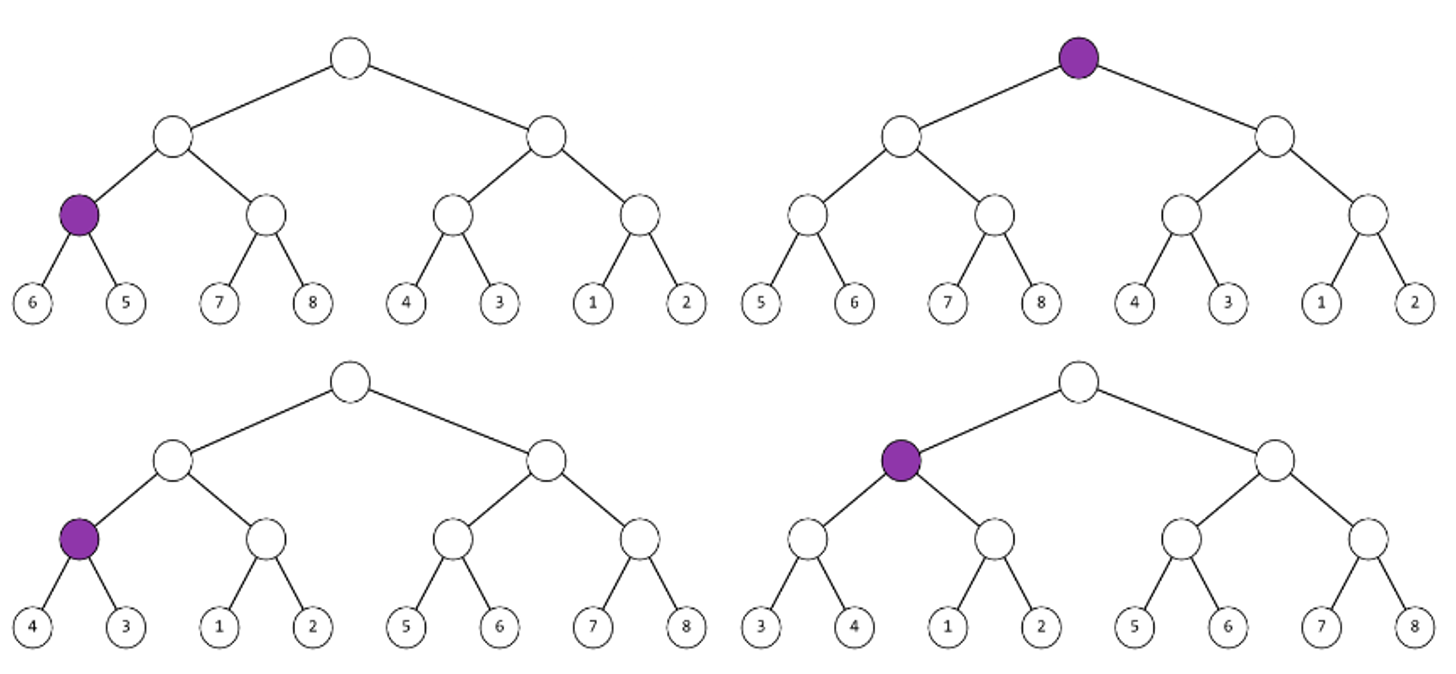
Consider another example, assume you have a complete binary tree of height 4, and the leaf numbers are 6, 5, 7, 8, 4, 3, 1, 2 (from left to right). Then, you can perform the following operations (the node that the operation is applied at the current step is highlighted in purple) to make permutation P sorted (in increasing order from left to right).
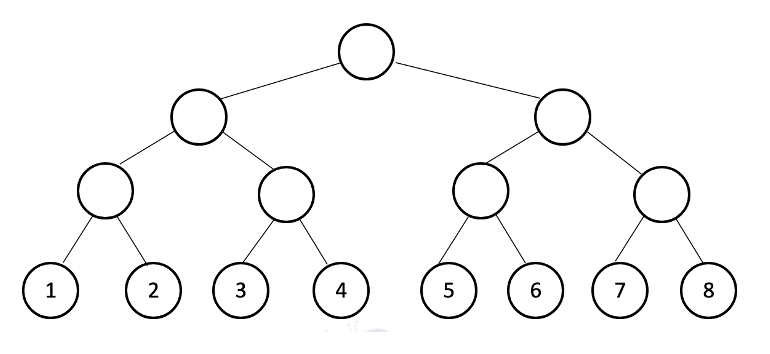
After all operation, permutation P should be like this.
You job is to output the minimum number of operations to make permutation P sorted in ascending order from left to right.
Input
The first line contains a single integer t (1<t<10000), which is the number of test cases.
In each test case, the first line contains an integer n (1< n < 270000), which is a power of two, denoting the size of the permutation P.
The second line contains n integers: p1,p2,…,pn (1≤pi≤n), indicating the left numbers from left to right.
Total n will not exceed 3*10^6 in each test case.
Output
For each test case in a separate line, print the minimum number of operations to make it sorted. If this is not possible, print -1.