Description
The CS student association held a Christmas party for students with other departments. In the party, each boy invited a girl to be his dance partner. When entering the ballroom, each of them picked up a roll of colored ribbon. The boys then lined up in one single row in the order of their arrival.
Girls then entered the ballroom and picked up the other end of the color ribbon from the boys and stretched the ribbon as they lined up in a parallel row of boys. When everyone was set, there are one row of N boys and the other row of N girls, with N ribbons that paired them.
The party host wanted to select some pairs for the first dance. The host decided to cut off the least number of ribbons to make the remaining ribbons not crisscrossed. Then those pairs were selected. In the below example, 4 pairs were selected for the first dance by way of cutting off 2 ribbons. Note that 4 pairs is also the maximum that can be achieved in the example. Given different arrival configurations, your task is to the maximum pairs could be selected for the first dance.
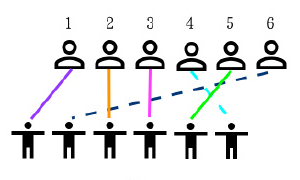
Hint
Look at the figure above. The above row are boys where \(i=0,1,2,3,4,5\), while the below row are girls, where \(a_i=0,5,1,2,4,3\).
First it's obvious for us to observe that if we select girl \(a_i\) (e.g. \(a_2=5\)), then we couldn't select greater \(a_i\) afterwards since it would result in crisscross. That is, we must always select some increasing ones.
Furthermore, to find the answer of this problem, we could rather find all the answers that the last girl we select is \(a_i\). In this way, we have that it is the maximum of the answers of girls before and less than her.
Eventually, for any boy \(i\), if \(\exists j, a_j<a_i\) and the answer of \(a_j\) is less than \(a_i\), then we would never select \(a_i\). Again, the ones we select always increasing.
Input
For each test case, the first line contains one integer, \(N\), where \(N<10^6\), indicating the number of boys. The second line contains \(N\) distinct integers, ranged from \(0\) to \(N-1\). The first integer \(i\) menas that the first boy invited the \(i^{th}\) girl to dance and so on.
In \(40\%\) of test cases, \(N<5000\). In \(20\%\) of test cases, \(N<200\).
Output
Print out the number of pairs selected for the first dance. Remember to print a newline character at the end.