Description
This problem uses partial judge. Please select gcc compiler when submitting.
A binary search tree is a binary tree that has the following properties:
-
For any node, its key is greater than the keys stored in the left subtree.
-
For any node, its key is smaller than the keys stored in the right subtree.
-
For any node, the left subtree and the right subtree are binary search trees respectively as well.
-
Every node has a unique key. No two nodes share the same key.
For example, the two following trees are binary search trees.
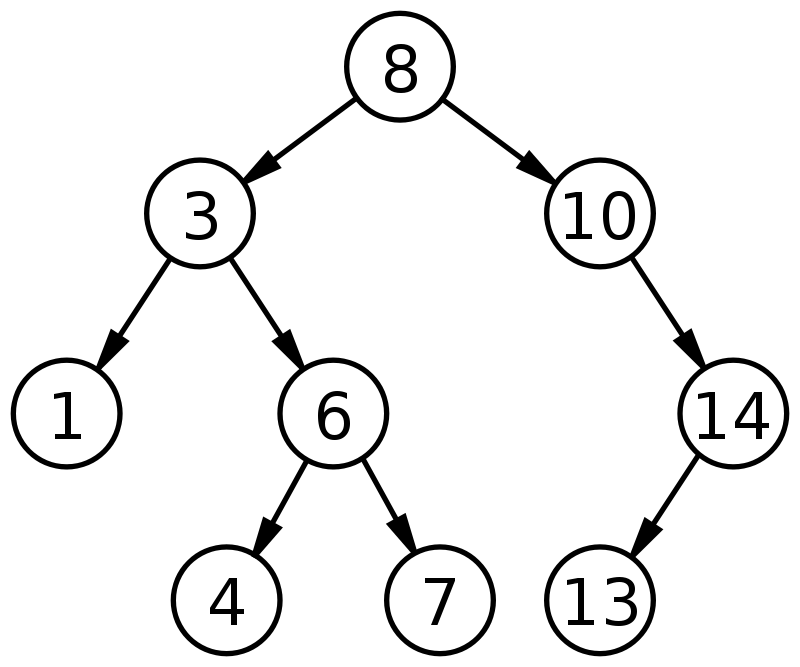
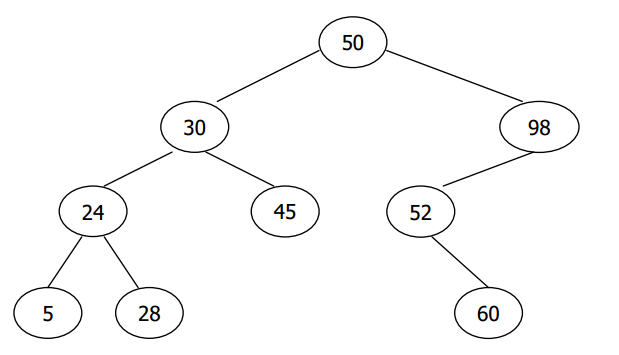
Given the pre-order traversal of a binary search tree, please output the in-order traversal and post-order traversal of the binary search tree. It can be proven that for no two binary search tree shares the same pre-order traversal.
Input
The first line is an integer T, meaning that there are T test cases in a single input file.
For each test case, the first line is an integer N, denoting the size of the binary search tree. The next line are N integers, denoting the pre-order traversal of the binary search tree.
-
1 <= T <= 2000
-
1 <= N <= 106
-
1 <= N x T <= 2 x 106
-
Be careful of memory leak
-
To pass all test cases, try to come up with an O(N) algorithm to build the binary search tree.
-
-
0 <= key of node <= 109
Output
For each test case, please output two lines: The first line is the in-order traversal of the binary search tree. The second line is the post-order traversal of the binary search tree.
Note that there is a space after each output number. e.g. use printf("%d ", var_to_be_printed) when printing.