| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14850 | The Skyline Problem |
|
| 14863 | K-th biggest element in a binary search tree |
|
| 14864 | Map Color |
|
| 14865 | Employee Network Query System |
|
| 14866 | The Winner of the Circular Game (Josephus problem) |
|
Description
(30 points)
HARD HARD HARD HARD HARD
The skyline of a city is the outer contour (外輪廓) formed by all the buildings when viewed from a distance. You are given several rectangular buildings, and your task is to compute the key points that form the skyline.
Each building is represented as a triplet [Li, Ri, Hi] where:
-
Liis the x-coordinate of the left edge, -
Riis the x-coordinate of the right edge, -
Hi is the height of the building.
All buildings sit on a flat ground at height 0.
You must return the skyline formed by these buildings as a list of key points. A key point [x,y] represents a position where the skyline height changes from the previous height.
The key points must be sorted by increasing x-coordinate, and redundant horizontal points (same height continuing) must not be included.The final skyline should reflect the exact outer contour as viewed from left to right.
HINT
Here is part of the solution. Please complete the TODO sections.
#include <stdlib.h>
#include <stdio.h>
// Structure to represent an edge (start or end of a building)
typedef struct {
int x;
int height;
int type; // 1 for start edge, 0 for end edge
} Edge;
// Comparison function for qsort to sort edges
int compareEdges(const void* a, const void* b) {
Edge* edgeA = (Edge*)a;
Edge* edgeB = (Edge*)b;
if (edgeA->x != edgeB->x) {
return edgeA->x - edgeB->x;
}
// If x-coordinates are the same, handle edge types:
// Start edges (type 1) with higher height come first
// End edges (type 0) with lower height come first
if (edgeA->type == 1 && edgeB->type == 1) {
return edgeB->height - edgeA->height;
}
if (edgeA->type == 0 && edgeB->type == 0) {
return edgeA->height - edgeB->height;
}
return edgeB->type - edgeA->type; // Start edges before end edges
}
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both the returned array and *returnColumnSizes array must be malloced,
* assume caller calls free().
*/
int** getSkyline(int** buildings, int buildingsSize, int* buildingsColSize,
int* returnSize, int** returnColumnSizes) {
if (buildingsSize == 0) {
*returnSize = 0;
return NULL;
}
// Step 1: create start / end edges for all buildings
Edge* edges = (Edge*)malloc(sizeof(Edge) * buildingsSize * 2);
int edgeCount = 0;
for (int i = 0; i < buildingsSize; ++i) {
edges[edgeCount++] = (Edge){buildings[i][0], buildings[i][2], 1}; // start edge
edges[edgeCount++] = (Edge){buildings[i][1], buildings[i][2], 0}; // end edge
}
// Step 2: sort edges by x coordinate and edge type
qsort(edges, edgeCount, sizeof(Edge), compareEdges);
// Allocate result arrays (maximum possible size = number of edges)
int** result = (int**)malloc(sizeof(int*) * edgeCount);
*returnColumnSizes = (int*)malloc(sizeof(int) * edgeCount);
*returnSize = 0;
/* ========================= TODOs start here ========================= */
// TODO 1:
// Sweep from left to right through the sorted edges.
// TODO 2:
// Maintain a data structure that keeps track of the heights of
// all "active" buildings (buildings that have started but not ended yet).
// TODO 3:
// When encountering a start edge, add its height to the active set.
// When encountering an end edge, remove its height from the active set.
// TODO 4:
// Important: if multiple edges share the same x coordinate,
// process ALL of them before deciding whether to output a skyline point.
// TODO 5:
// After processing all edges at position x,
// find the current maximum height among active buildings.
// TODO 6:
// If the current maximum height is different from the previous one,
// output a key point (x, current maximum height) and update the previous height.
/* ========================== TODOs end here ========================== */
free(edges);
return result;
}
int main(void)
{
int n;
// Input format:
// n
// L0 R0 H0
// L1 R1 H1
// ...
// Ln-1 Rn-1 Hn-1
if (scanf("%d", &n) != 1) {
return 0;
}
int **buildings = (int **)malloc(sizeof(int*) * n);
int *buildingsColSize = (int *)malloc(sizeof(int) * n);
for (int i = 0; i < n; ++i) {
buildings[i] = (int *)malloc(sizeof(int) * 3);
int L, R, H;
if (scanf("%d %d %d", &L, &R, &H) != 3) {
for (int k = 0; k <= i; ++k) {
free(buildings[k]);
}
free(buildings);
free(buildingsColSize);
return 0;
}
buildings[i][0] = L;
buildings[i][1] = R;
buildings[i][2] = H;
buildingsColSize[i] = 3;
}
int returnSize;
int *returnColumnSizes;
int **skyline = getSkyline(buildings, n, buildingsColSize,
&returnSize, &returnColumnSizes);
// Print result
// Each line: x y
for (int i = 0; i < returnSize; ++i) {
printf("%d %d\n", skyline[i][0], skyline[i][1]);
}
// Free memory
for (int i = 0; i < n; ++i) {
free(buildings[i]);
}
free(buildings);
free(buildingsColSize);
if (skyline != NULL) {
for (int i = 0; i < returnSize; ++i) {
free(skyline[i]);
}
free(skyline);
}
if (returnColumnSizes != NULL) {
free(returnColumnSizes);
}
return 0;
}
Input
-
The input is a 2D integer array
buildings. -
The first line is the number of buildings
-
Each element
buildings[i] = [Li, Ri, Hi]describes:-
Li: the x-coordinate of the building’s left boundary
-
Ri: the x-coordinate of the building’s right boundary
-
Hi: the height of the building
-
-
Constraints:
-
0 ≤ Li< Ri
-
Hi > 0
-
-
Buildings may overlap.
Take Sample Input 1 as example,
Each line contains three integers described as above. We can visulized in the Figure 1.
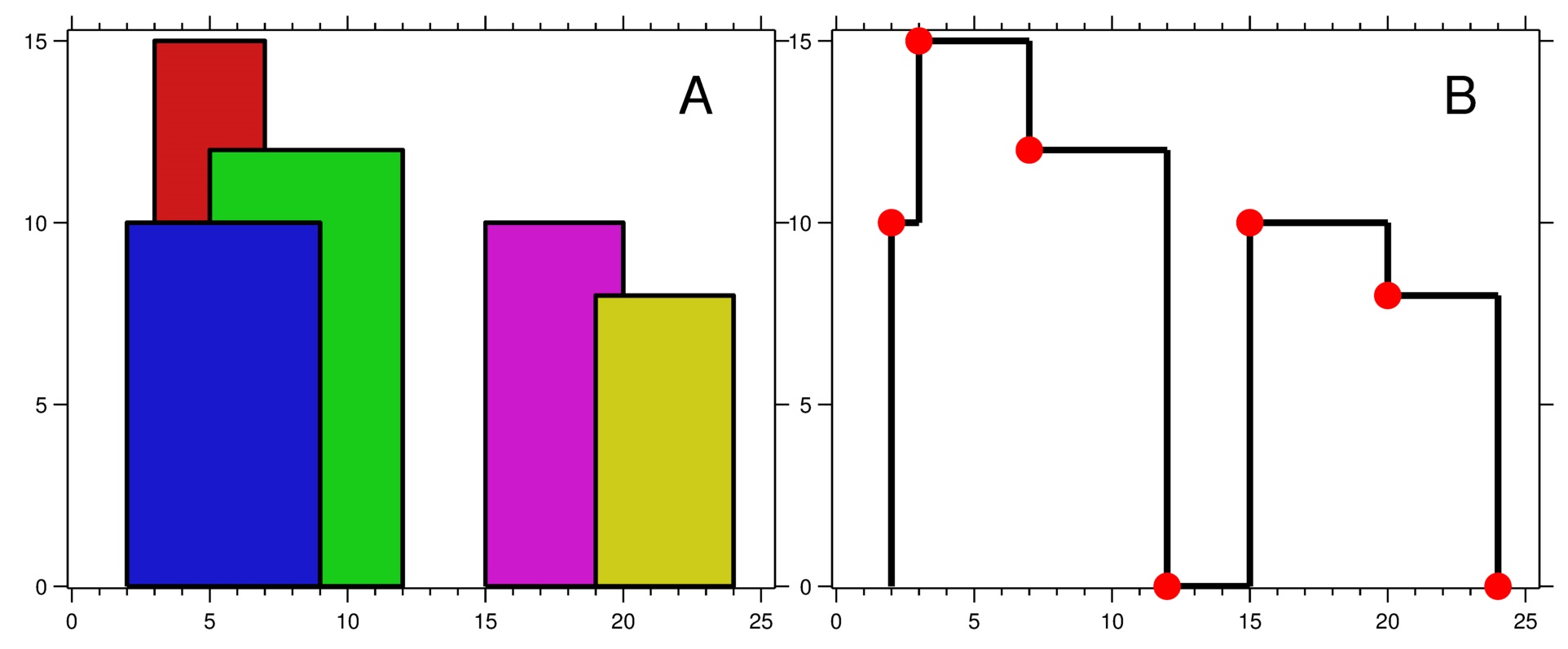
Figure 1
Output
-
Output a 2D integer array
skyline. -
Each element
skyline[j] = [xj, yj]is a key point, indicating the skyline height becomesyjat x-coordinatexj. -
Requirements:
-
Key points must be sorted by increasing
xj. -
Do not include multiple points with the same height in a row. Only include points where the height actually changes.
-
The skyline typically ends with a point whose height becomes 0.
-
The Sample Output 1 can be inllustrated as Figure 1.
Note that There must be no consecutive horizontal lines of equal height in the output skyline.
The following instance is not acceptable;
2 3 4 5 7 5 11 5 12 7
the three lines of height 5 should be merged into one in the final output as such
2 3 4 5 12 7
Sample Input Download
Sample Output Download
Tags
Discuss
Description
(20 points)
You are given a sequence of integers. These integers are inserted into a Binary Search Tree (BST) one by one, in the given order.
After the BST is constructed, you will receive several queries. Each query contains an integer k, and you must determine the value of the node that is the k-th biggest element in the entire BST.
The BST insertion rule follows the standard definition:
-
If a value is less than or equal to the node, it is inserted into the left subtree.
-
Otherwise, it is inserted into the right subtree.
Each query asks for the element ranked k-th when all nodes are sorted in ascending order.
A completed program of BST structure and insertion is provided. You only need to write the function:
BS_Tree *find_kth_max_data (BS_Tree *root, int k)
so that it correctly returns the pointer to the k-th smallest node.
Given C code (complete the marked part):
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define debug 0
typedef struct bs_tree {
int data;
int sub_node_count;
struct bs_tree *left;
struct bs_tree *right;
}BS_Tree;
BS_Tree *find_kth_max_data (BS_Tree *root, int k){
/*
Written by yourself
*/
}
BS_Tree *insert_sort_BS_Tree(BS_Tree *root, int data){
BS_Tree *current = root;
if (root == NULL) {
current = (BS_Tree *) malloc (sizeof(BS_Tree));
assert(current != NULL);
if (debug) printf("malloc (BS_Tree *) at %p\n", current);
current->data = data;
current->left = NULL;
current->right = NULL;
return current;
}
if (data <= current->data)
current->left = insert_sort_BS_Tree(current->left, data);
else
current->right = insert_sort_BS_Tree(current->right, data);
return current;
}
int insert_sub_node_count (BS_Tree *root){
int left_count, right_count, total_count;
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) {
root->sub_node_count = 1;
return 1;
}
left_count = insert_sub_node_count(root->left);
right_count = insert_sub_node_count(root->right);
root->sub_node_count = 1 + left_count + right_count;
return root->sub_node_count;
}
void print_inorder (BS_Tree *root){
if (root == NULL) return ;
print_inorder(root->left);
printf("%d %d\n", root->data, root->sub_node_count);
print_inorder(root->right);
}
BS_Tree *delete_BS_Tree(BS_Tree *root){
if (root == NULL) return NULL;
delete_BS_Tree(root->left);
delete_BS_Tree(root->right);
if (debug) printf("free (BS_Tree *) at %p\n", root);
free(root);
return NULL;
}
int main (void){
int data, k;
BS_Tree *root = NULL;
BS_Tree *ptr_kth_min;
do {
scanf("%d", &data);
if (debug) printf("input data %d\n", data);
root = insert_sort_BS_Tree(root, data);
}while (getchar() != '\n');
insert_sub_node_count(root);
if (debug) print_inorder(root);
do {
scanf("%d", &k);
if (debug) printf("input k = %d\n", k);
ptr_kth_min = find_kth_min_data(root, k);
printf("%d\n", ptr_kth_min->data);
}while (getchar() != '\n');
root = delete_BS_Tree(root);
return 0;
}
The following figure shows the tree structure for Sample Input 1.
The input data can be formatted using the function insert_sub_node_count(root).
The number next to each node represents the total number of nodes in its subtree.
Input
First line: n integers, representing the values to be inserted into the BST.
Second line: m integers, each representing a query k.
Constraints:
-
0 < n ≤ 100000 -
0 < m ≤ n -
1 ≤ k ≤ n
Output
Output m lines. Each line contains the data of the node that is the k-th biggest value in the BST corresponding to each query.
Ensure the output formatting exactly matches the required samples.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
(20 points)
Write a program to color the countries of a map.
A map contains n countries, and we want to determine whether it is possible to use c colors so that no two adjacent countries share the same color.
Each country has a unique ID from 1 to n, and each color has a unique ID from 1 to c.
Input
-
Line 1: Three integers
n c p
where
-
n = number of countries
-
c = number of available colors
-
p = number of adjacent country pairs
-
-
Next p lines: Each line contains two integers
i j
meaning that country i and country j are adjacent and therefore cannot have the same color.
Output
-
If a valid coloring exists, output n integers, separated by spaces.
The k-th integer represents the assigned color of country k. -
Among all possible valid colorings, output the lexicographically smallest sequence.
-
If no valid coloring exists, output:
no solution
Sample Input Download
Sample Output Download
Tags
Discuss
Description
(20 points)
You are given information about a group of employees in a company.
Each employee is represented by the following structure:
typedef struct {
int id; // unique employee ID
char firstname[32]; // first name
char lastname[32]; // last name
int boss_id; // direct supervisor's employee ID
} employee;
-
Each employee has a unique ID (
id). -
boss_idstores the direct supervisor’s ID. -
If an employee’s
boss_idis the same as their ownid, that employee is the top-level boss. -
All employees and their supervisors are guaranteed to appear in the input.
You will receive several queries.
Each query specifies an employee’s full name and an integer k.
Depending on the value of k, you must perform one of the following operations:
k = 1 — Print all of their colleagues
Print all employees who share the same direct supervisor as the queried employee
(excluding the employee themself and excluding the top-level boss).
Example
Query: James Vance 1
Output: Ching-te Lai
k = 2 — Print their supervisors (from nearest to farthest)
Print the chain of supervisors starting from the employee’s direct boss,
then that boss’s boss, and so on, until reaching the top-level boss.
Each supervisor is printed on its own line as:
Example
Query: Miku Hatsune 2
Output: James Vance Donald Trump
k = 3 — Print their subordinates (from nearest to farthest)
Print all employees who are under the queried employee in the hierarchy.
-
First print all direct subordinates of the queried employee.
-
Then, for each of those subordinates, print their subordinates recursively.
-
When there are multiple subordinates at the same level, you must always process the one with the smaller index in the input list first.
In other words, among all employees who have the same boss, visit them in ascending order of their array index (0, 1, 2, …).
Each subordinate is printed on its own line as:
Example
Query:
Donald Trump 3
Suppose the input order is:
-
Miku Hatsune
-
James Vance
-
Donald Trump
-
Ching-te Lai
Then the output should be: James Vance Miku Hatsune Ching-te Lai
Here:
-
James VanceandChing-te Laiare direct subordinates ofDonald Trump. -
Miku Hatsuneis a subordinate ofJames Vance. -
Since
James Vancehas a smaller index thanChing-te Lai, his subtree is printed first:-
James Vance -
then his subordinate
Miku Hatsune
-
-
Then the subtree of
Ching-te Lai(who has no subordinates) is printed.
Hint
For k = 1, two employees are colleagues if they have the same boss_id (and are not the same person).
For k = 2, starting from the queried employee, repeatedly move to their boss (using boss_id) until you reach the top-level boss.
For k = 3, starting from the queried employee, recursively find all employees whose boss_id matches this employee’s id.
Here is a Pseudo-code for k = 3 condition,
function DFS_Subordinates(employees, n, boss_index):
for i from 0 to n-1:
if employees[i].boss_id == employees[boss_index].i and employees[i].id != employees[i].boss_id:
print employees[i].firstname, employees[i].lastname
// Recursively process this subordinate
DFS_Subordinates(employees, n, i)
function print_subordinate(employees, n, employee_index):
if employee_index < 0:
return
DFS_Subordinates(employees, n, employee_index)
Input
-
The first line contains an integer n, the number of employees.
-
The next n lines each contain four values describing one employee:
id firstname lastname boss_id
-
The following line contains an integer m, the number of queries.
-
Each of the next m lines contains a query in the form:
firstname lastname k
where firstname lastname identifies the employee being queried, and k specifies the operation to perform.
You may assume that all queried employees appear in the employee list.
Output
For each query, output a list of employees according to the value of k:
-
k = 1
Print all colleagues of the queried employee — that is, all employees who share the same direct supervisor, excluding the employee themselves and excluding the top-level boss. -
k = 2
Print the supervisors of the queried employee, starting from the nearest (direct boss) and moving upward through the hierarchy until reaching the top-level boss. -
k = 3
Print all subordinates of the queried employee.
First print all direct subordinates, followed by their subordinates, and so on recursively (from nearest to farthest).
Each employee is printed on its own line in the format:
firstname lastname
If no employees satisfy the query (e.g., no colleagues, no supervisors, or no subordinates), print nothing for that query.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
(30 points)
There are n friends playing a game. They sit in a circle and are numbered from 1 to n in clockwise order.
You are also given an integer k. The game starts from friend 1, and proceeds according to the following rules:
-
Moving clockwise from the i-th friend brings you to friend (i + 1) for all 1 ≤ i < n, and moving clockwise from friend n brings you back to friend 1.
Game Rules
-
Start at friend 1.
-
Count k friends in the clockwise direction, including the current friend as the first count.
The counting wraps around the circle as necessary. -
The friend who is counted as the k-th leaves the circle and is eliminated from the game.
-
If more than one friend remains, the next round starts from the friend immediately clockwise of the one who was just eliminated, and the process repeats.
-
When only one friend remains, that friend is declared the winner.
Task
Given the integers n and k, return the label of the friend who wins the game.
For Example,
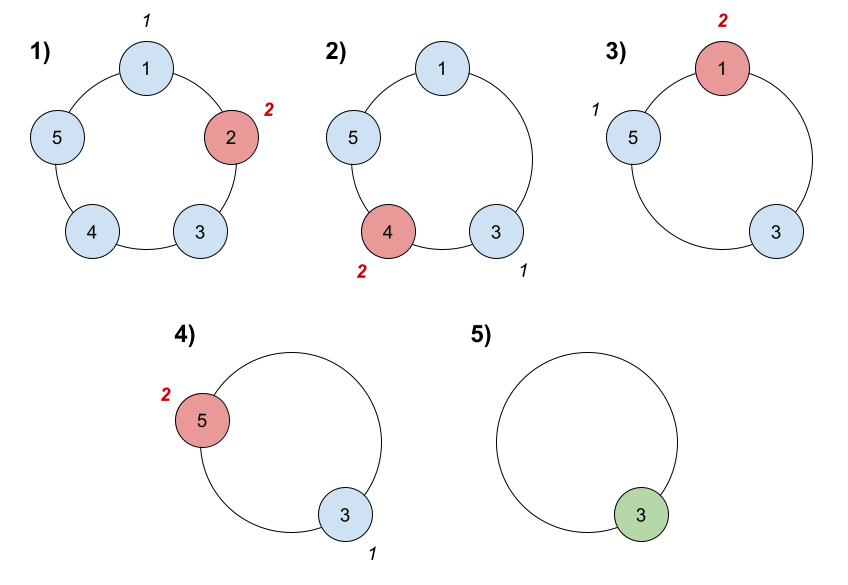
Input: n = 5, k = 2 Output: 3 Explanation: Here are the steps of the game: 1) Start at friend 1. 2) Count 2 friends clockwise, which are friends 1 and 2. 3) Friend 2 leaves the circle. Next start is friend 3. 4) Count 2 friends clockwise, which are friends 3 and 4. 5) Friend 4 leaves the circle. Next start is friend 5. 6) Count 2 friends clockwise, which are friends 5 and 1. 7) Friend 1 leaves the circle. Next start is friend 3. 8) Count 2 friends clockwise, which are friends 3 and 5. 9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
For more Information about this problem, you can read it after the exam.
Note that the problem is named after Flavius Josephus, a Jewish historian and leader who lived in the 1st century. According to Josephus's firsthand account of the siege of Yodfat, he and his 40 soldiers were trapped in a cave by Roman soldiers. They chose suicide over capture, and settled on a serial method of committing suicide by drawing lots. Josephus states that by luck or possibly by the hand of God, he and another man remained until the end and surrendered to the Romans rather than killing themselves. (The above descriptions are from wikipedia and it is the case that n = 41 and k = 5, where the last two survivors are numbered 16 and 31, you can take this as the input/output case. )
Input
-
An integer n — the number of people in the circle.
-
An integer k — the counting step.
-
Constraints:
1 ≤ k ≤ n ≤ 500
Output
Return the label (1 to n) of the only person left in the circle, who becomes the winner of the game.