| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14750 | Wordle |
|
| 14753 | Stair Sum |
|
| 14759 | Learning Linear Programming |
|
Description

Let's play Wordle!!!
You are given an answer string $S$ of length $n$ (all lower-case letters).
Then you will receive an integer $q$.
For each of the next $q$ lines, you are given a guess string $T$ of length $n$ (all lower-case letters).
For each guess, output a feedback string of length $n$ using the following symbols:
G(Green): the letter matches the answer at the same position.Y(Yellow): the letter occurs in the answer but in a different position (respecting letter counts).B(Black): the letter does not occur in the answer in any unmatched position.
Important (duplicate letters):
A letter in the guess can only be marked G or Y as many times as it appears in the answer.
If the guess has extra occurrences beyond what the answer contains, the extra ones are marked B.
Example with abbey:
- Answer =
abbey - Guess =
bobby
Step 1 (mark greens): positions 3 (b) and 5 (y) are exact matches → ??G?G.
Step 2 (check yellows with remaining letters, from left to right):
- Guess position 1 =
b→ still onebleft in answer → markY. - Guess position 2 =
o→ not in answer → markB. - Guess position 4 =
b→ nobleft in answer → markB.
Final result: YBGBG.
Input
- Line 1: a string $S$ — the hidden answer ($\lvert S \rvert = n$, lower-case a–z).
- Line 2: an integer $q$ — the number of guesses.
- Next $q$ lines: each line contains a string $T$ — the guess ($\lvert T \rvert = n$, lower-case a–z).
Constraints
- $1 \leq n \leq 2 \times 10^4$
- $1 \leq q \leq 50$
All strings consist only of lower-case English letters a–z.
Subtask
For testcases 1~5:
- $1 \leq n \leq 1000$
For testcases 6~10:
- No additional constraints.
Output
For each guess, output a line with a string of length $n$ over the alphabet {G, Y, B} indicating the feedback for that guess.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given a integer sequence (a1, a2, ..., an) of length n.
In this problem, you need to answer q quiries, each query is of the form:
- l r
Meaning you need to answer the sum of al * 1 + al+1 * 2 + al+2 * 3 + ... + ar-1 * (r - l) + ar * (r - l + 1).
Contraints
- 1 <= n <= 105
- 0 <= ai < 232, i = 1, 2, ..., n
- All ai s are integer
- For each query, 1 <= l <= r <= n
Subtask
- Testcase 1~3: n <= 1000
- Testcase 4~6: No additional constraints
Input
The first line contains an integer n: the length of the sequence.
The second line contains n integers a1, a2, ..., an, each integer is seperated by a blank.
The third line contains an integer q: the number of queries you need to answer.
For the next q line, each line contains two integer l r, seperated by a blank.
Output
For each query, print the answer in one line.
Hint
For the first query in the sample input, the answer should be a1 * 1 + a2 * 2 + a3 * 3 = 1 * 1 + 1 * 2 + 4 * 3 = 15. For the second query, the answer should be a5 * 1 + a6 * 2 = 1 * 1 + 2 * 4 = 9.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear relationships. (by wikipedia)
In a linear programming problem, there will be many linear inequality constraints of the form ax+by<=c. We call a point (x, y) is in the feasible region of this problem if (x, y) satisfies all the linear inequality constraints.
For example, consider the following five constraints:
- -5x + 2y <= 1
- y <= 5
- -x - y <= 1
- 3x <= 11
- 3x - 2y <= 2
Then (1, 1) and (1.6, 1.8) is in the feasible region, since they satisfy all the constraints above. However, (2, 1.5) is not in the feasible region, as it doesn't satisfy the fifth constraint. The red area in the following picture shows the feasible region of these contraints.
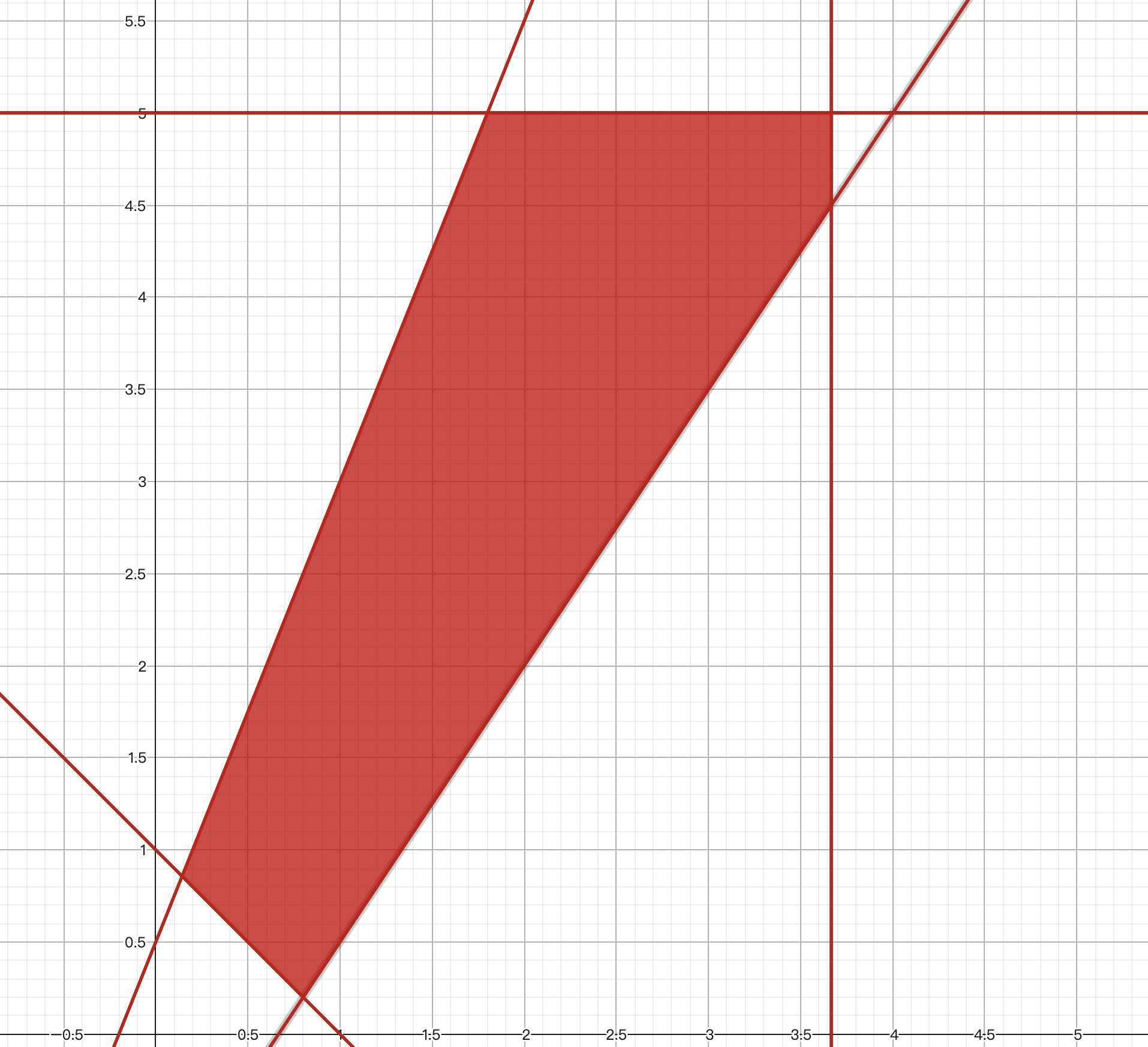
In this problem, you are given n such constraints, and you need to answer how many integer points are there in the feasible region. Note that a point (x, y) is called an integer point if both of x, y are integers.
Input
The first line contains an integer T, meaning there are total T testcase in the input.
For each testcase, the first line contains one integer n: the number of constraints.
For the next n lines, each line contains three integers a, b, c (separated by blanks), meaning there is a linear inequality constraint ax + by <= c.
Output
Output an integer in one line: the number of integer points in the feasible region.
Contraints
- 1 <= T <= 5
- 1 <= n <= 800
- 0 <= |a|, |b|, |c| <= 232-1
- It is guranteed that at least one of a, b is non-zero.
- It is guaranteed that all the points (x, y) in the feasible region safisfy: 0 <= x <= 1000, 0 <= y <= 1000
Subtask
- Testcase 1~5: n <= 100, all the points (x, y) in the feasible region safisfy: 0 <= x <= 100, 0 <= y <= 100
- Testcase 6~8: No additional constraints
Hint
The sample testcase is exactly the example in the problem description.