| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14745 | Potato's Password III |
|
| 14752 | Tug of War |
|
| 14754 | Hang man |
|
Description
LeeFuuChang the Potato once saw a way to generate password by combining numbers from a grid in a certain pattern.
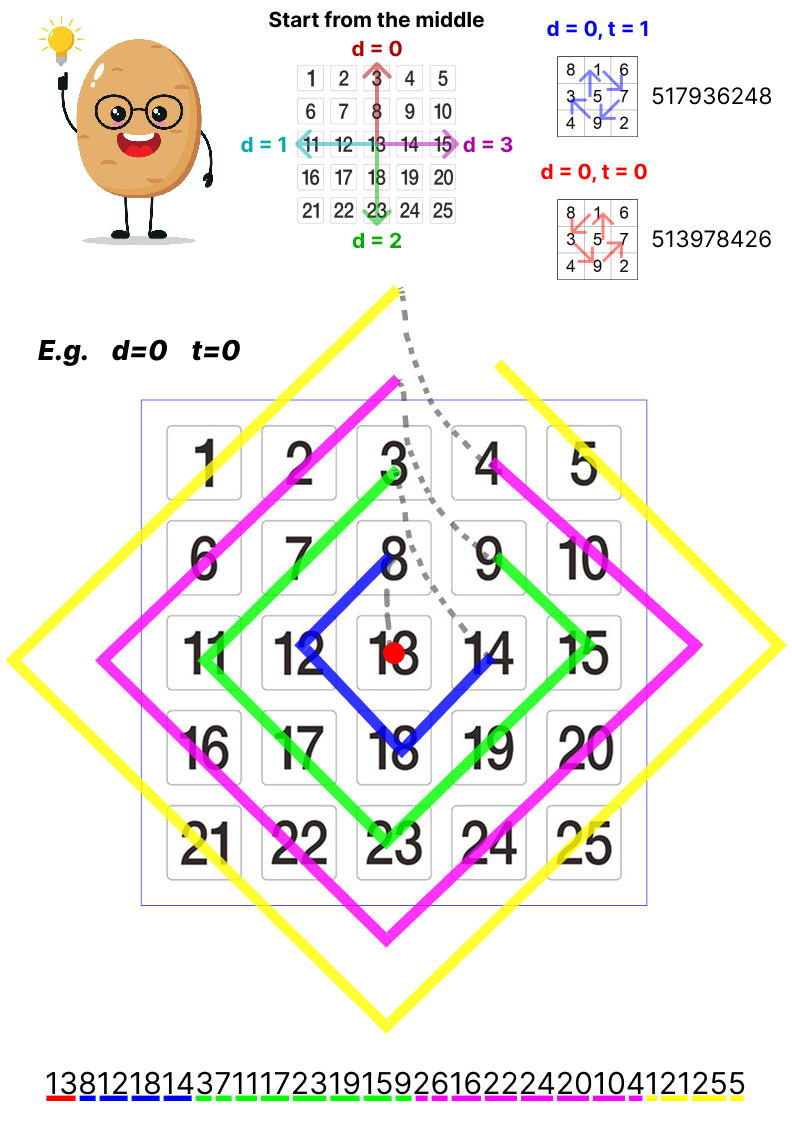
So you, as a kind and generous student, wanted to help Potato finish the program that does the transformation from grid to password.
Feel free to use the following code as a starter.
def solve(n, d, t, grid):
"""
This is the explanation of the template code
We've read the input for you.
this function will take in 4 parameters:
- n:
a integer representing the size of the grid
- d:
a integer representing the starting direction
- t:
a integer representing the rotating direction
- grid:
a 'nxn' grid filled with integers
a.k.a, for any grid[i][j] is int
you need to return a string that satisfies the problem's requirement.
Feel free to delete this explanation after reading it.
"""
ans = ""
# your
# code
# here
return ans
_n, _d, _t = map(int, input().split())
_grid = []
for _ in range(_n):
_row = []
for num in input().split():
_row.append(int(num))
_grid.append(_row)
print(solve(_n, _d, _t, _grid))
Potato judges your code by the following limitations:
- Testcase 1:
n = 3,d = 0,t = 1 - Testcase 2 ~ 3:
n <= 29,d ∈ {0, 1, 2, 3},t = 1 - Testcase 4 ~ 5:
n <= 29,d = 0,t ∈ {0, 1} - Testcase 6:
n <= 59,d ∈ {0, 1, 2, 3},t ∈ {0, 1}
Potato's Whisper: If you take a closer look at the 25 grid above:
- the 2-nd cycle always take 1 steps before turn
- the 3-rd cycle always take 2 steps before turn
- the 4-th cycle always take 3 steps before turn
- and so on...
Input
First line contains 3 integers n,d,t representing:
- The size of the grid is
nxn - Start walking the spiral facing
ddirection ( Upd=0| Leftd=1| Downd=2| Rightd=3) - The spiral goes clockwise
t=1or counter-clockwiset=0
Each of the following n lines contains n integers, forming a nxn grid.
It's guaranteed that:
n%2 == 11 <= n <= 59d ∈ {0, 1, 2, 3}t ∈ {0, 1}0 <= grid[i][j] <= n*n
Output
Output the password formed by the order of traversing the grid, with no space between numbers, and a newline at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Elephants are not only cute but also love to compete in tug of war.
The rules of the game are simple:
- The team must contain at least one elephant;
- The total weight of the team must be divisible by $k$.
elfnt, the coach of the NTHU elephant team, has $n$ elephants standing in a line. the weight of the $i$-th elephant is $x_i$. to keep things fair, a team must be chosen as a contiguous segment of elephants in that line.
Your task is to help elfnt count how many different teams can be formed that satisfy the rules above.
Formally, count the number of pairs $(l, r)$ with $1 \le l \le r \le n$ such that
$$ (x_l + x_{l+1} + \dots + x_r) \equiv 0 \pmod{k} $$
Input
The first line contains an integers $n$.
The second line contains an integers $k$.
The third line contains $n$ integers $x_1, x_2, \dots, x_n$, where $x_i$ is the weight of the $i$-th elephant.
Constraints
- $1 \le n \le 10^6$
- $1 \le x_i \le 10^9$
- $1 \le k \le 10^9$
Subtask
- (Testcases 1-2) $1 \leq k \leq n \leq 100$
- (Testcases 3-5) $1 \leq k \leq n \leq 1000$
- (Testcases 6-7) $1 \leq k \leq n$
- (Testcase 8) No additional constraints.
Output
Print the answer followed by a newline.
Hint
In the sample test case
Valid teams include:
- $(1,3)$: $1+1+4=6 \equiv 0\ \pmod{3}$
- $(1,5)$: $1+1+4+5+1=12 \equiv 0\ \pmod{3}$
- $(2,6)$: $1+4+5+1+4=15 \equiv 0\ \pmod{3}$
- $(3,4)$: $4+5=9 \equiv 0\ \pmod{3}$
- $(4,5)$: $5+1=6 \equiv 0\ \pmod{3}$
Thus, there are $5$ possible teams.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
elfnt wants to practice his English vocabulary, so Momo designed a word guessing game (AKA The hang man game) for him.
The rules are as follows:
- elfnt has exactly $k$ chances to perform operations.
-
In each chance, he may choose one of the following operations:
-
check
c- Check if the letter
cexists in the hidden word. (uppercase) - If yes, reveal all occurrences of
cin the word. - If not, nothing happens.
- After executing this operation, print the current revealed word status (letters +
_).
- Check if the letter
-
guess
word- Guess that the hidden word is exactly
word. - If the guess is correct, print
You winand terminate the game. - Otherwise, print
Wrong.
- Guess that the hidden word is exactly
-
chance
- Display the number of remaining chances.
- This operation does NOT consume a chance.
-
hint
- Reveal the leftmost unrevealed letter in the word.
- If the same letter appears elsewhere, reveal all of them at once.
- This operation can only be used once in the entire game.
- If used more than once, output
Already used(does NOT consume a chance). - If the entire word has already been fully revealed, using
hintstill consumes the one-time chance (if not used) but does not reveal anything new. - After executing this operation, print the current revealed word status (letters +
_).
- Each valid operation (
check,guess, or first-timehint) consumes one chance. - The operation
chanceand repeatedhintdo not consume any chance. - If all $k$ chances are consumed without guessing the correct word, output
You loseand terminate.
Input
- The first line contains an integer $n$ — the length of the hidden word.
- The second line contains an integer $k$ — the number of chances elfnt has.
- The third line contains the hidden word consisting of $n$ uppercase English letters.
- Starting from the fourth line, each subsequent line describes an operation until the game ends.
- Each operation is one of the following forms:
check cguess wordhintchance
Constraints
- $1 \le n \le 1000$
- $1 \le k \le 2000$
- The
chanceand repeatedhintoperations does not exceed $2000$ times. - The hidden word contains only uppercase English letters (
A–Z).
Subtasks
- (Testcases 1–4) No
hintoperation. - (Testcases 5–6) No additional constraints.
Output
Follow the rules strictly:
- After a
checkor validhint, print the status. (letters +_). - After a
guess, printYou winif correct and terminate immediately; otherwise printWrong. - After a
chancecommand, print the remaining number of chances (without consuming any). - If
hintis repeated, printAlready used(without consuming a chance). - When all chances are consumed without winning, print
You lose.

