| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14749 | Absolute Cinnamoroll |
|
| 14751 | Reorder Distance |
|
Description
You only need to solve up to 6/8 accepted.
The last two testcases are left as an exercise since it requires a minor optimization. (These two NOT be covered in the midterm exam.)



elfnt has many Cinnamorolls, and he wants to choose four of them to decorate his room depending on today’s happy value $n$.
Each Cinnamoroll has a size number, and elfnt possesses all different sizes of Cinnamorolls, with four of each size.
The happy value is calculated as $a \times b \times c + d$. elfnt wants to know how many ways are there to choose the Cinnamorolls when today's happy value is $n$.
Formally, find the number of quadruples $(a, b, c, d)$ of positive integers such that:
$$ a \times b \times c + d = n $$
Input
A single integer $n$.
Constraints
$2 \leq n \leq 5 \cdot 10^7$
Subtask
- (Testcase 1) $2 \leq n \leq 50$
- (Testcase 2) $2 \leq n \leq 100$
- (Testcase 3) $2 \leq n \leq 1000$
- (Testcases 4-6) $2 \leq n \leq 10^6$
- (Testcase 7) $2 \leq n \leq 5 \cdot 10^6$
- (Testcase 8) No additional constraints.
Output
Print the number of quadruples $(a, b, c, d)$ of positive integers satisfying the condition and followed by a new line.
Hint
When $n = 4$, all valid quadruples $(a,b,c,d)$ are:
$$ (1,1,1,3),\; (1,1,2,2),\; (1,1,3,1),\; (1,2,1,2),\; (2,1,1,2),\; (1,3,1,1),\; (3,1,1,1) $$ Hence, there are $7$ valid quadruples in total.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given two strings s, t of same length, you need to find the reorder distance between them.
Let us define the reorder distance between two strings of same length to be the minimum number of positions that has different character after reordering the strings (that is, arranging the characters in the string).
For example, the reorder distance between "yajusenpai" and "pineapples" is 4, as we can reorder the first string into "pineayajus". In this way, only four position of these two strings has different character (position 6 to 9).
For the formal definition, let [n] be the set {1, 2, 3, ..., n}, where n is the length of strings, and F be the set of all bijections between [n] and [n]. Then the reorder distance of s, t, denoted as d(s, t), is:
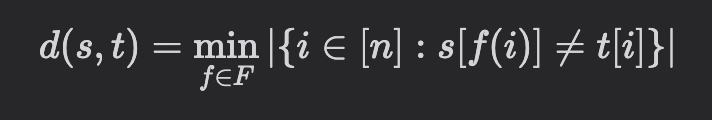
Input
The first line is the string s, and the second line is the string t.
It is guranteed that these two string are of same length, and the length will not exceed 105. Also, the input strings only contain lowercase english letters.
Output
Output the reorder distance between two strings in one line.