| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14739 | Mirror Room with −45° Mirrors |
|
| 14740 | Spiral Traversal |
|
| 14742 | Calculate the distance between two points |
|
| 14743 | Counting the number of coprime numbers |
|
| 14744 | Roots of a quadratic equation |
|
Description
This problem is revised from example 6.26 of the textbook.
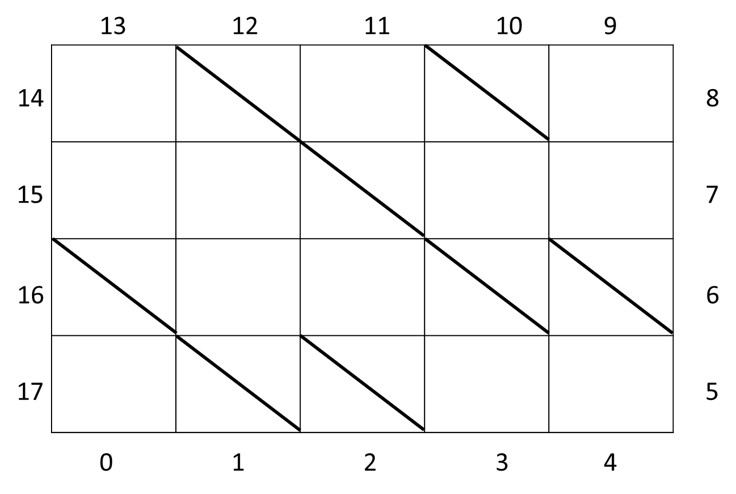
We place a number of two-sided mirrors at a −45° angle ("\" orientation) inside a rectangular room of width W and depth D.
The room boundary contains 2 × (W + D) windows, numbered in counterclockwise order starting from 0 at the bottom edge.
When a light ray enters the room from one window, it travels straight through the grid.
-
If the ray passes through an empty cell (
0), it continues in the same direction. -
If the ray encounters a mirror (
1), it is reflected according to the −45° mirror rule:-
Down → Right
-
Right → Down
-
Up → Left
-
Left → Up
-
The ray will eventually leave the room through another boundary window.
Your task is to simulate the ray’s path and determine, for each entry window, the corresponding exit window.
Input
-
The first line contains two integers W and D — the width and depth of the room.
-
The next D lines each contain W integers (0 or 1).
-
1means the cell contains a −45° mirror ("\"). -
0means the cell is empty.
-
-
The arrangement of the room can be seen in the following figure of Sample Input 1.
Constraint
1 ≤ W, D ≤ 500
Output
-
Print 2 × (W + D) lines.
-
The i-th line contains the window number where a ray entering from window i will exit.
Sample Input Download
Sample Output Download
Discuss
Description
This problem is revised from example 6.27 of the textbook.
You are given an n x n matrix, where n is an odd integer.
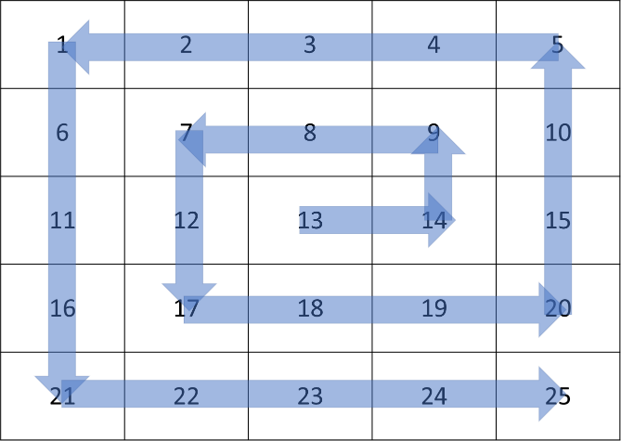
Starting from the center of the matrix, traverse all elements in a counterclockwise spiral path.
The traversal must follow these rules:
-
Direction order:
Right → Up → Left → Down→ (repeat). -
Step lengths:
-
The number of steps in each direction follows the sequence 1,1,2,2,3,3,…
-
Each step length is repeated twice (for two consecutive directions).
-
The only exception is the last step length (n−1), which must be repeated three times to complete the outer boundary.
-
-
Traversal stops when all n2 elements have been visited exactly once.
Sample Input/Output 2 can be visualized in the following figure.
Input
-
The first line contains an odd integer n (1≤n≤99).
-
The next n lines each contain nnn integers, representing the matrix elements in row-major order.
Output
Print the elements of the matrix in the order they are visited by the spiral traversal, one element per line.
Sample Input Download
Sample Output Download
Discuss
Description
Write a program to calculate the distance between two points, where the points are represented in polar coordinates as (r1, θ1) and (r2, θ2).
The input consists of one line containing r1, θ1, r2, and θ2.
The output is the distance between the two points. Note that we need to use the sin and cos functions, so we must include math.h.
When compiling with gcc, remember to add -lm to link the math library.
Input
Two points expressed in polar coordinates.
Ex. 10 0.0 10 3.1415926
Output
The distance between the two points.
Ex.20.000000
Sample Input Download
Sample Output Download
Discuss
Description
Refer to Example 5.5 and write a program to calculate how many pairs of numbers are coprime among n given numbers.
We can rewrite Example 5.5 into a function to determine whether two numbers are coprime, which will speed up program development.
The input consists of one line containing n positive integers.
The output is the number of pairs of coprime numbers among these n integers.
Constraint: 0 < n <= 100
Example 5.5 Calculate the greatest common factor of i and j #include <stdio.h> main() { int i, j, k; scanf("%d", &i); scanf("%d", &j); while (i % j != 0) { k = i % j; i = j; j = k; } printf("%d\n", j); } Input 72 56 Output 8
Input
A line of n positive integers.
Ex. 23 76 34 12 7 5 34
Output
Numbers of pairs of numbers among these n positive integers that are coprime.
Ex. 16
Sample Input Download
Sample Output Download
Discuss
Description
Write a program to calculate the roots of a quadratic equation. First, read three coefficients: a, b, and c. Then calculate the two roots of the equation ax2+bx+c=0.
Assume that b2−4ac>0, so there are two real roots.
The output should display the two roots, with the smaller one first and the larger one second.
Input
The three coefficients of a quadratic equation (arranged in descending order)
Ex. -1.0
1.0
6.0
Output
Roots of a quadratic equation (output smaller ones first, then larger ones)
Ex. -2.000000
3.000000