| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14722 | Potato's Password I |
|
| 14728 | Word Puzzle |
|
Description
LeeFuuChang the Potato once saw a way to generate password by combining numbers from a grid in a certain pattern.
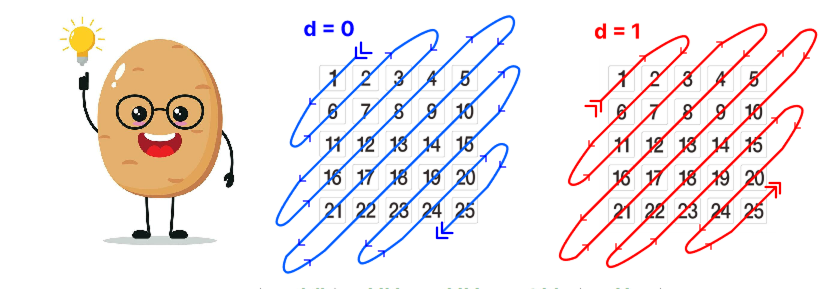
So you, as a kind and generous student, wanted to help Potato finish the program that does the transformation from grid to password.
Feel free to use the following code as a starter.
def solve(n, d, grid):
"""
This is the explanation of the template code
We've read the input for you.
this function will take in 3 parameters:
- n:
a integer representing the size of the grid
- d:
a integer representing the starting direction
- grid:
a 'nxn' grid filled with integers
a.k.a, for any grid[i][j] is int
you need to return a string that satisfies the problem's requirement.
Feel free to delete this explanation after reading it.
"""
ans = ""
# your
# code
# here
return ans
_n, _d = map(int, input().split())
_grid = []
for _ in range(_n):
_row = []
for num in input().split():
_row.append(int(num))
_grid.append(_row)
print(solve(_n, _d, _grid))
Potato judges your code by the following limitations:
- 20%:
n <= 11,d = 0 - 20%:
n <= 11,d = 1 - 20%:
n <= 29,d = 0 - 20%:
n <= 29,d = 1 - 20%:
n <= 59,d ∈ {0, 1}
Potato's whisper: it is HIGHLY suggested to NOT use list in solving this problem, since list WON'T help you solve the actual midterm problem, but finding the pattern WILL.
Input
First line contains 2 integers n,d representing:
- The size of the grid is
nxn - Start slicing the grid with
ddirection ( refer to the image besides TA.Potato )
Each of the following n lines contains n integers, forming a nxn grid.
It's guaranteed that:
1 <= n <= 59d ∈ {0, 1}0 <= grid[i][j] <= n*n
Output
Output the password formed by the order of traversing the grid, with no space between numbers, and a newline at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given a source string $S$, an integer $k$, and a target string $T$.
Determine whether there exists a contiguous substring of S with length $k$ whose characters can be rearranged to form $T$, you can left some characters unused.
If such a window exists, print YES; otherwise, print NO.
Input
- Line 1: the source string $S$
- Line 2: the integer $k$
- Line 3: the target string $T$
Constraints
- $1 \leq \lvert S \rvert, \lvert T \rvert \leq 2 \times 10^5$
- $0 \leq k \leq 2 \times 10^5$
Subtask
For testcases 1~5:
- $1 \leq \lvert S \rvert, \lvert T \rvert \leq 1000$
- $0 \leq k \leq 1000$
For testcases 6~10:
- No additional constraints.
Output
Print YES if there exists a contiguous substring of $S$ with length $k$ whose characters can be rearranged to form $T$ (possibly with extra unused characters in the window).
Otherwise, print NO.