| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14336 | Divisor Jumps |
|
| 14629 | KuoTA Restaurant 3 |
|
| 14635 | KuoTA Hotel |
|
Description
There are \(N\) stones, numbered \(1,2,...,N\).
There is a frog who is initially on Stone \(x\). He will repeat the following action some number of times to reach Stone \(N\):
- If the frog is currently on Stone \(i\), jump to Stone \(i + d\) or Stone \(i - d\) where \(d\) is a divisor of \(i\).
Here, an integer \(b\) is said to be a divisor of \(a\) if there exist an integer \(c\) such that \(a = b \times c\).
For each starting stone \(1 \leq x \leq N\), find the minimum number of jumps to reach Stone \(N\).
Input
The only line contains an integer \(N\).
\(N\)
Constraints
- \(1 \le N\le 10^6\)
Output
Please output \(N\) integers in a line, each followed by a space.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Elephants love to eat KuoTA (鍋貼), so Elfnt decided to open a restaurant called "八方來財", serving delicious KuoTA to satisfy their cravings.
Now that Elfnt knows how to calculate the duration the restaurant needs to stay open, he hopes to minimize his working hours. He already knows the dining time of all $n$ elephants today. Please help him determine the minimum number of seats required so that the restaurant can close within $k$ units of time (including $k$).
As long as there is an available seat, the customer at the front of the queue will immediately be seated and start dining. Once the $i$-th customer is seated, they will occupy the seat for $x_i$ units of time, after which they will leave the restaurant, freeing up the seat.
It is guaranteed that the answer must exists.
Input
The first line contains two integers $n$ and $k$, representing the number of elephants and the maximum allowed time units before the restaurant closes.
The second line contains $n$ integers $x_1, x_2, ..., x_n$, where $x_i$ is the amount of time the $i$-th elephant will take to dine.
Constraints
- $1 \leq n \leq 2 \times 10^5$
- $1 \leq x_i \leq 1000$
- $1 \leq k \leq \sum_{i=1}^{n}x_i$
Subtask
- (Testcases 1-5) $1 \leq n \leq 1000$
- (Testcases 6-8) No additional constraints.
Output
Output the minimum number of seats required to ensure that all elephants can finish dining within $k$ units of time. (NO space and '\n' at the end)
Sample Input Download
Sample Output Download
Tags
Discuss
Description
KuoTA's hotel has an infinite number of rooms. The manager wants to keep track of how many customers are there in his hotel. The $i$-th customer checks in at the $s_i$-th day and stay for $l_i$ consecutive days, in other words, the room will be occcuied on days $s_i$, $s_i+1$, ..., $s_i+l_i-1$. Since KuoTA is too busy launching his new business "八方來財", your task is to help him compute, for each possible occupancy level $k$ (where $k$ ranges from $1$ to $N$), calculate how many days exactly $k$ rooms are occupied simultaneously.
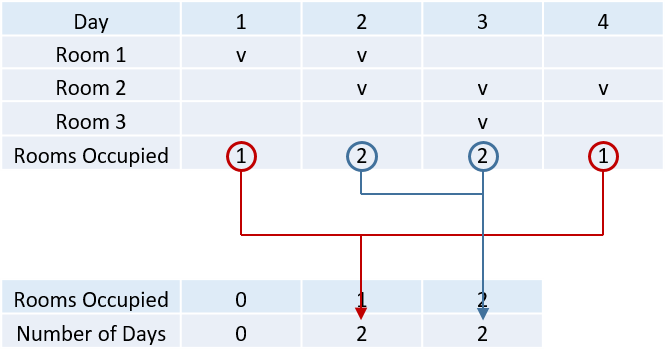
Input
The first line contain an integer $N$, the total number of customers.
Following are $N$ lines, each contain two integer $s_i$ and $l_i$, representing the day when i-th customer will check in and how long he will stay resepectively.
$N$
$s_1 \quad l_1$
$s_2 \quad l_2$
$\quad\vdots$
$s_N \quad l_N$
Constraints
- $1 \leq N \leq 2 \cdot 10^5$
- $1 \leq s_i, l_i, s_i+l_i-1 \leq 10^9$
Subtasks
- (Testcases 1~4): $N, s_i+l_i-1 \leq 3 \cdot 10^3$
- (Testcases 5~6): $s_i+l_i-1 \leq 2 \cdot 10^5$
- (Testcases 7~8): No additional constraint
Output
Output one single line containing $N$ integers, the $i$-th integer (1-based) is the total number of days that exactly $i$ rooms are occupied.