| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13236 | easy 8 Puzzles (English version) |
|
| 13237 | Wolf, goat and cabbage |
|
| 13451 | K-th largest |
|
| 13532 | Promenade Dance |
|
| 14336 | Divisor Jumps |
|
| 14628 | KuoTA Restaurant 2 |
|
| 14637 | Point Domination |
|
Description
Note: This is just the translation of "10664 - easy 8 Puzzles" in English. Please submit your code to "10664 - easy 8 Puzzles".
Given a 3×3 board with 9 tiles and every tile has one number from 0 to 8.
| 1 | 2 | 3 |
| 4 | 0 | 5 |
| 7 | 8 | 6 |
We can swap ‘0’ with its four adjacent (left, right, above, and below) tiles. For example:
step 1 : swap 0 with ‘5’
| 1 | 2 | 3 |
| 4 | 5 | 0 |
| 7 | 8 | 6 |
step 2 : swap 0 with ‘6’
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 0 |
The objective is to place the numbers on tiles to match the following configuration.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 0 |
(Noting important in this paragraph, something like Rody is too busy and needs your help to solve this problem.)
Input
Given T (1<=T<=30) in the first line, saying that there will be T test cases.
From 2nd line to (T+1)-th line, each line contains 9 distinct integers from 0 to 8, representing an 8-puzzle game. Nice integers will be filled to the 3×3 board in a row-major manner. For example, 1 2 3 4 0 5 7 8 6 will become the configuration as shown in the following figure.
| 1 | 2 | 3 |
| 4 | 0 | 5 |
| 7 | 8 | 6 |
Output
For each 8-puzzle game, if it can be solved in 14 steps, print out "You can solve it within x steps.", x is the minimum number of steps to solve this puzzle. Otherwise, print out "You'd better skip this game.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Notice: You need to enable the flag -std=c++11 to compile the code!
- In codeblocks, go to Settings->Compiler->check the option "Have g++ follow the C++11 ISO C++ language standard [-std=c++11]"->OK
- In dev-c++, go to Tools->Compiler options->check "Add the following commands ..."->type in "-std=c++11"(without qoute) ->OK
Once upon a time a farmer went to a market and purchased X wolfs, Y goats, and Z cabbages.
On his way home, the farmer came to the left river bank and rented a boat. To cross the river by a boat, the farmer could carry only himself and at most one of his purchases: a wolf, a goat, or a cabbage.
At both left and right banks, if the farmer is not there and the wolves are more than the goats (#W>#G), the wolves will eat the goats. Also, if the farmer is not there and the goats are more than the cabbages (#G>#C), the goats will eat the cabbages.
In this problem, you have to find all solutions that the farmer can carry himself and all his purchases from the left to the right bank.
For each solution, you cannot produce duplicate states.
For example:
(0, 1, 1)(0, 1, 0) right
(0, 1, 1)(0, 1, 0) left
(0, 0, 1)(0, 2, 0) right
(0, 1, 1)(0, 1, 0) left
(0, 0, 1)(0, 2, 0) right
(0, 0, 1)(0, 2, 0) left
(0, 0, 0)(0, 2, 1) right
done
This solution isn't allowed because there are duplicate states.
Hint: You can use set<State> _explored to store each state.
Input
The input has only single line containing three integer X Y Z, representing the number of purchased wolves, goats and cabbages.
Output
List all solutions one by one.
"Done" denotes the end of a solution.
A solution contains several moves. Each move is represented by a line with the format of:
(#W at the left, #G at the left, #C at the left)(#W at the right, #G at the right, #C at the right) [left/right]
W: wolf, G: goat, C: cabbage, left/right: position of the boat.
For example:
(0, 1, 1)(0, 1, 0) right
(0, 1, 1)(0, 1, 0) left
(0, 0, 1)(0, 2, 0) right
(0, 0, 1)(0, 2, 0) left
(0, 0, 0)(0, 2, 1) right
done
We've created the function to print outputs from the variable set, so you just need to add your solutions to the variable set<list<State>> _solutions. You don't have to worry about the order of your solutions.
Sample Input Download
Sample Output Download
Partial Judge Code
13237.cppPartial Judge Header
13237.hTags
Discuss
Description
Mr. Kuo is an adventurer. One day, he finds a sequences of operations and an empty set S.
Each operation is one of the following two types,
- Insert x:insert x into S. Duplicate element is legal.
- Query x k:Among the elements of S that are greater or equal to x, what is the k-th smallest value?
Mr. Kuo is curious about the answer to each operation 2, so he asks for your help.
Hint:You can refer to C++ upper_bound function.
Input
The input consists of multiple lines.
Each line is given in one of the following two format:
- Insert x
- Query x k
There will be at most 100000 operations in the sequences.
1 ≤ x ≤ 109
1 ≤ k ≤ 5
Output
For each operation of type 2, print the k-th smallest value among the elements of S that are greater than or equal to x.
If there are less than k elements of S that are greater than or equal to x, then print "-1".
Remember to print '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The CS student association held a Christmas party for students with other departments. In the party, each boy invited a girl to be his dance partner. When entering the ballroom, each of them picked up a roll of colored ribbon. The boys then lined up in one single row in the order of their arrival.
Girls then entered the ballroom and picked up the other end of the color ribbon from the boys and stretched the ribbon as they lined up in a parallel row of boys. When everyone was set, there are one row of N boys and the other row of N girls, with N ribbons that paired them.
The party host wanted to select some pairs for the first dance. The host decided to cut off the least number of ribbons to make the remaining ribbons not crisscrossed. Then those pairs were selected. In the below example, 4 pairs were selected for the first dance by way of cutting off 2 ribbons. Note that 4 pairs is also the maximum that can be achieved in the example. Given different arrival configurations, your task is to the maximum pairs could be selected for the first dance.
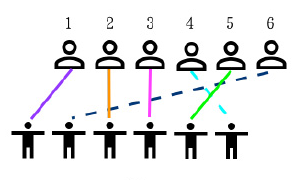
Hint
Look at the figure above. The above row are boys where \(i=0,1,2,3,4,5\), while the below row are girls, where \(a_i=0,5,1,2,4,3\).
First it's obvious for us to observe that if we select girl \(a_i\) (e.g. \(a_2=5\)), then we couldn't select greater \(a_i\) afterwards since it would result in crisscross. That is, we must always select some increasing ones.
Furthermore, to find the answer of this problem, we could rather find all the answers that the last girl we select is \(a_i\). In this way, we have that it is the maximum of the answers of girls before and less than her.
Eventually, for any boy \(i\), if \(\exists j, a_j<a_i\) and the answer of \(a_j\) is less than \(a_i\), then we would never select \(a_i\). Again, the ones we select always increasing.
Input
For each test case, the first line contains one integer, \(N\), where \(N<10^6\), indicating the number of boys. The second line contains \(N\) distinct integers, ranged from \(0\) to \(N-1\). The first integer \(i\) menas that the first boy invited the \(i^{th}\) girl to dance and so on.
In \(40\%\) of test cases, \(N<5000\). In \(20\%\) of test cases, \(N<200\).
Output
Print out the number of pairs selected for the first dance. Remember to print a newline character at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are \(N\) stones, numbered \(1,2,...,N\).
There is a frog who is initially on Stone \(x\). He will repeat the following action some number of times to reach Stone \(N\):
- If the frog is currently on Stone \(i\), jump to Stone \(i + d\) or Stone \(i - d\) where \(d\) is a divisor of \(i\).
Here, an integer \(b\) is said to be a divisor of \(a\) if there exist an integer \(c\) such that \(a = b \times c\).
For each starting stone \(1 \leq x \leq N\), find the minimum number of jumps to reach Stone \(N\).
Input
The only line contains an integer \(N\).
\(N\)
Constraints
- \(1 \le N\le 10^6\)
Output
Please output \(N\) integers in a line, each followed by a space.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You might need to use long long int to avoid overflow.
Elephants love to eat KuoTA (鍋貼), so Elfnt decided to open a restaurant called "八方來財", serving delicious KuoTA to satisfy their cravings.
After solving the queueing problem, Elfnt now hopes to close the restaurant as early as possible to get some rest. He already knows the dining time of all $n$ elephants today. Please calculate how long the restaurant needs to stay open, from opening to closing.
There are $k$ seats in the restaurant. As long as there is an available seat, the elephant at the front of the queue will immediately be seated and start dining. Once the $i$-th elephant is seated, they will occupy the seat for $x_i$ units of time, after which they will leave the restaurant, freeing up the seat. (At the very beginning, the first $k$ elephants will be seated immediately.)
Input
The first line contains two integers $n$ and $k$, representing the number of elephant and the number of seats.
The second line contains $n$ integers $x_1, x_2, ..., x_n$, where $x_i$ is the amount of time the $i$-th elephant will take to dine.
Constraints
- $1 \leq n, k \leq 2 \times 10^5$
- $1 \leq x_j \leq 10^9$
Subtask
- (Testcases 1-3) $1 \leq n, k \leq 1000$
- (Testcases 4-6) No additional constraints.
Output
Output how long the restaurant needs to stay open. (NO space and '\n' at the end)
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given $N$ distinct points on the 2D plane, your task is to compute, for each point $(x_i, y_i)$, how many other points dominate this point. We say point $(x_a, y_a)$ dominates point $(x_b, y_b)$ if and only if $x_a \geq x_b$ and $y_a \geq y_b$
- Hint: Binary Indexed Tree (BIT) might be useful: you can refer to page 96 of this book for BIT implementation detail.
Input
The first line contains an integer $N$, the number of points.
Each of the next $N$ lines contains two integers, $x_i$ and $y_i$, the coordinates of the $i$-th point.
$N$
$x_1 \quad y_1$
$x_2 \quad y_2$
$\quad\vdots$
$x_N \quad y_N$
Constraints
- $1 \leq N \leq 2 \cdot 10^5$
- $1 \leq x_i, y_i \leq 10^9$
- All points $(x_i, y_i)$ are distinct
Subtasks
- (Testcases 1~6): $N, x_i, y_i \leq 3 \cdot 10^3$
- (Testcases 7~8): No additional constraint
Output
Output a single line with $N$ integers. The $i$-th integer should be the number of points that dominate the $i$-th point