| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13483 | Beautiful subsequence |
|
| 13879 | Tree-Graph Inheritance |
|
| 13928 | Largest Rectangle |
|
| 14587 | Good memory |
|
| 14631 | Portal |
|
Description
Given a sequence A = a1, a2, ..., aN and a number K.
A continuous subsequence A[L ... R] = aL, ..., aR of A is called beautiful if the sum of A[L ... R] is K.
For example, if A = 3, 1, 2, 2, 4 and K = 6.
Then
- A[1, 3] = 3, 1, 2 is beautiful.
- A[1, 4] = 3, 1, 2, 2 is not beautiful because 3 + 1 + 2 + 2 is not 6.
- A[4, 5] = 2, 4 is beautiful.
Please find the number of beautiful continuous subsequence of A.
Input
The first line of the input contains a number T — the number of test cases.
The first line of each test case contains two numbers N K — the length of A and the number K described in the statement.
The second line of each test case contains N numbers — a1, a2, ..., aN.
For each test,
- T ≤ 10, N ≤ 103, |ai| ≤ 109, |K| ≤ 109.
- T ≤ 10, N ≤ 103, |ai| ≤ 109, |K| ≤ 109.
- T ≤ 10, N ≤ 103, |ai| ≤ 109, |K| ≤ 109.
- T ≤ 10, N ≤ 105, |ai| ≤ 109, |K| ≤ 109.
- T ≤ 10, N ≤ 105, |ai| ≤ 109, |K| ≤ 109.
- T ≤ 10, N ≤ 105, |ai| ≤ 109, |K| ≤ 109.
Output
For each test case, print the number of beautiful continuous subsequence.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In Object-Oriented Programming (OOP), the inheritance among classes represent ``is-a'' relationships for abstractions. Graphs and trees are both fundamental for computer science. In fact, a tree is a special case of a graph that is connected as well as acyclic.
In fact, we often implement trees and graphs by similar means in practice. For instance, we tend to store trees and graphs by adjacent matrice or lists. Moreover, we traverse trees and graphs in alike ways.
For simplicity, we only consider basic operations on trees and graphs. You need implement BFS traversal for a graph starting from a given source and returning the distance to all other vertices so that trees could inherit that method. Furthermore, you should find the diameter (the longest distance in a tree that we've encountered several times but solved by DFS then) by BFS traversal.
Input
Please see the instructions in the header. BFS traversal would be called with the source. As for diameter, there's no parameter.
It's guaranteed that the graph is connected and simple, and that the number of vertices of a tree is less than 100000.
Output
For BFS traversal, you should return a vector of n integers indicating the minimum distance from source.
As for the diameter, you should return an integer.
Sample Input Download
Sample Output Download
Partial Judge Code
13879.cppPartial Judge Header
13879.hTags
Discuss
Description
There are N bars line up in a row. The height of the i-th bar is hi, and the width of each bar is 1. Please find the largest rectangle in it.
Sample test:
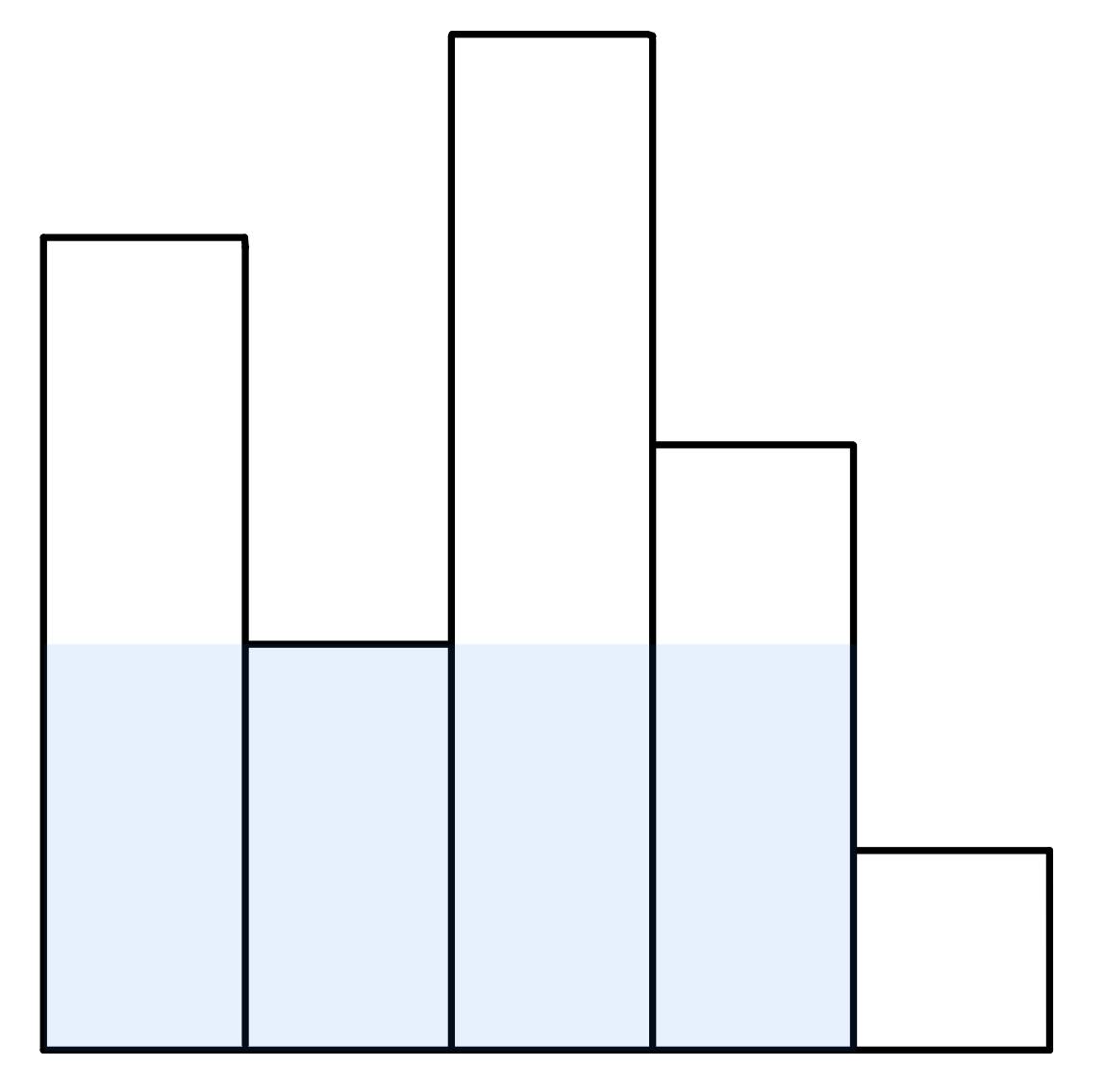
Input
The first line has an integer T, means there are T testcases.
The first line of each testcase contains an integer N, and the second line contains N integers h1 ~ hN.
1 <= hi <= 1e9.
1 <= T <= 10.
In testcase 1 ~ 4: 1 <= N <= 1000.
In testcase 5 ~ 8: 1 <= N <= 2e5.
Output
Please print the area of the largest rectangle for each testcase.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
We all know that elephants have incredible memory, as each one has a name and a lucky number.
elfnt can remember up to $n$ friends, storing them in his memory list.
There are $q$ queries, each belonging to one of the following types:
-
ASK name: Check if elfnt remembers an elephant with the givenname.- If found in memory, print its lucky number and refresh the impression of it by moving it to the front of the list.
- Otherwise, print
"Who?".
-
ADD name num: Introduce a new elephant withnameand lucky numbernum.- Otherwise, add it to the front of the list.
- If memory is full, remove the least recently used (ask or add) elephant before adding the new one.
It is guaranteed that NO same name will be added more than once using the ADD operation.

Input
The first line contains two integers $n$ and $q$, representing the size of the memory list and the query times.
The following $q$ lines, each contains a type of operation. The format are as follow.
ADD name numASK name
Constraints
- $1 \leq n \leq 5000$
- $1 \leq q \leq 2 \times 10^5$
- $1 \leq |$
name$| \leq 100$ - $1 \leq $
num$\leq 10^9$ - The
nameonly contains lowercase letters.
Subtask
- (Testcases 1-3) $1 \leq n, q \leq 1000$
- (Testcases 4-8) At most $2000$
ASKqueries. - (Testcases 9-10) No additional constraints.
Output
For each ASK query:
- Print the lucky number if
nameis found in memory. - Otherwise, print
"Who?".
Each output should be followed by a newline.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Let’s assume we are on a 1D map with coordinates ranging from 0 to 1e9.
There are $N$ portals and $M$ people who want to travel from one coordinate to another using the portals.
Each person begins at a specific starting coordinate and wants to travel to a specific destination.
For each person, you must find the nearest portal to their starting location and the nearest portal to their destination.
- If there are two portals equally close, choose the one with the smaller coordinate.
- If the nearest start and destination portals are the same, or if the total walking distance to reach the portals is greater than or equal to the direct walking distance from the start to the destination, the person will walk instead.
- Once a portal is used by person i, it is no longer available to any person after them.
Input
The first line contains two integers $N$ and $M$, representing the number of portals and the number of people.
The second line contains $N$ distinct integers $c_1, c_2, \dots, c_N$, where each $c_i$ is the coordinate of a portal.
It is guaranteed that all portals are located at distinct coordinates.
The next $M$ lines each contain two integers $s_i$ and $d_i$, representing the starting and destination coordinates of the $i$-th person.
Constraints
$1 \leq M \leq N \leq 2 \times 10^5$
$1 \leq c_i \leq 10^9$
$1 \leq s_i \leq d_i \leq 10^9$
Subtask
- (Test cases 1–3) $1 \leq N, M \leq 1000$
- (Test cases 4–6) No additional constraints.
Output
Output $M$ lines. For each person, output one of the following:
"walk", if walking is better or the start and the destination portals are the same.
Two integers — the coordinates of the nearest portal to the starting location and the nearest portal to the destination.