| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11443 | 3DShape |
|
| 13131 | Max-Heap Using Polymorphism |
|
| 13890 | Polynomial Calculator |
|
| 13891 | Polymorphic naming convention conversion |
|
| 14309 | Mixed Nuts |
|
Description
Warning: You are not allowed to use malloc and free
Giving a bass-class Shape3D and 4 derived class : Sphere (球體), Cone (圓錐), Cuboid (長方體), Cube (立方體)
You need to calculate the volume of each shape.
PS:
V of Sphere: V = 4/3 π r3
V of Cone: V = 1/3 π r2 h

note : Remember to do some basic check, if the input is illegal (e.g. length < 0, pi < 0 .....) then the volume should be 0.
You don't need to consider the scenario like Cuboid -1 -2 3, volume would be 0 instead of 6.
Hint1: Be careful the type of volume is double. 4/3=1 (int), so it should be 4.0/3.0
Hint2: You only need to implement the constructors.
Hint3: Note that Cube inherited Cuboid not Shape3D.
Input
There are only 4 shapes in this problem :
- Sphere, following by its radius and pi. (e.g. Sphere 30 3.14)
- Cone, following by its radius of bottom plane, height and pi. (e.g. Cone 3 100 3.14)
- Cuboid, following by its length, width and height. (e.g. Cuboid 2 3 7)
- Cube, following by its length. (e.g. Cube 2)
Output
Ouput the total volume of all the shapes.
Sample Input Download
Sample Output Download
Partial Judge Code
11443.cppPartial Judge Header
11443.hTags
Discuss
Description
A. Definition of Max-Heap
A heap is a complete binary tree.
A max-heap is a complete binary tree in which the value in each internal node is greater
than or equal to the values in the children of that node.
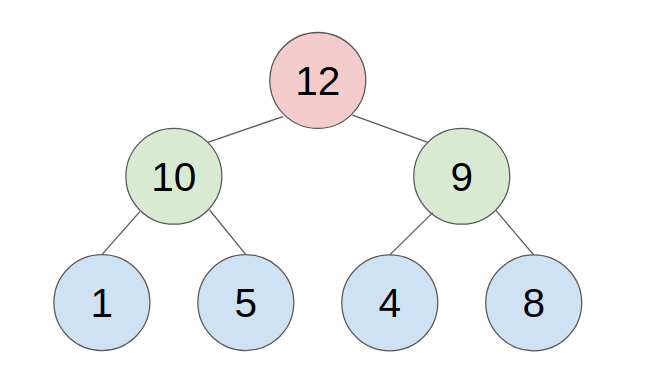
B. Implementation of the Max-Heap Data Structure
1. Array:
An approach to store a max-heap is to use a single, contiguous block of memory cells, i.e., an array, for the entire tree. We store the tree’s root node in the first cell of the array. (Note that, for ease of implementation, we ignore the 0th cell and start from the 1st cell.) Then we store the left child of the root in the second cell, store the right child of the root in the third cell, and in general, continue to store the left and right children of the node found in cell n in the cells 2n and 2n+1 respectively. With this technique, the tree shown below
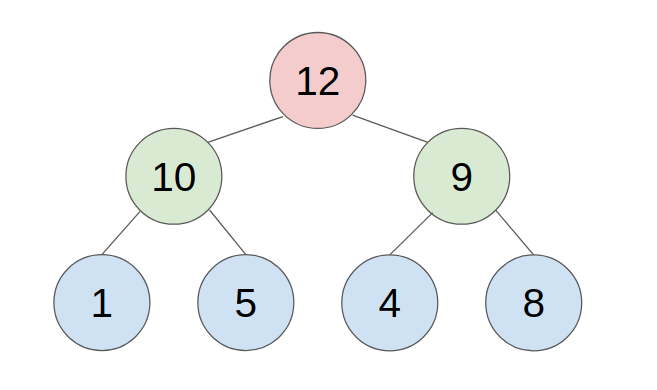
would be stored as follows

2. Linked list:
We set a special memory location, call a root pointer, where we store the address of the root node. Then each node in the tree must be set to point to the parent and left or right child of the pertinent node or assigned the NULL value if there are no more nodes in that direction of the tree.
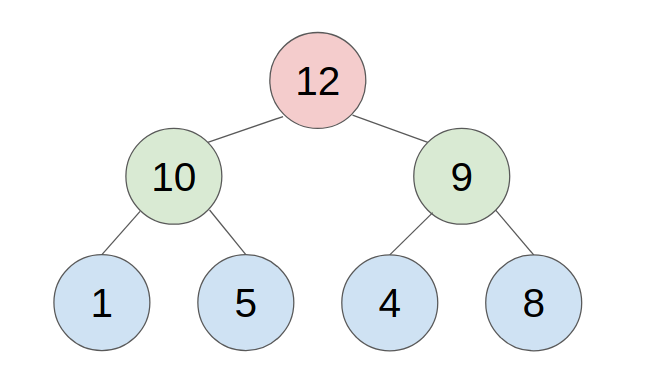
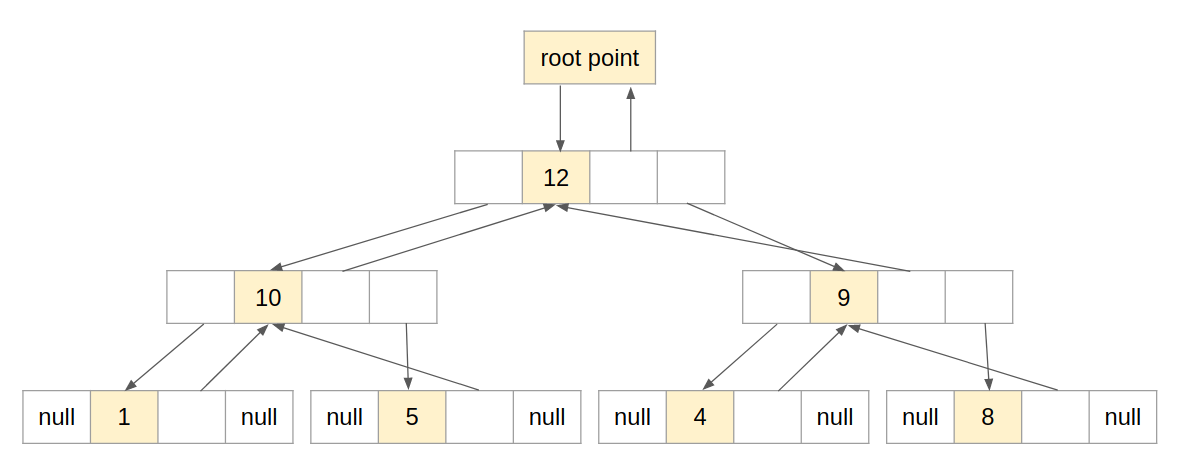
C. Method to push/pop an element
1. PUSH
- put the new element in the last place of the heap.
- compare with the parent, swap them until the parent is greater or equal to the new element.
- example: push 11 to this heap
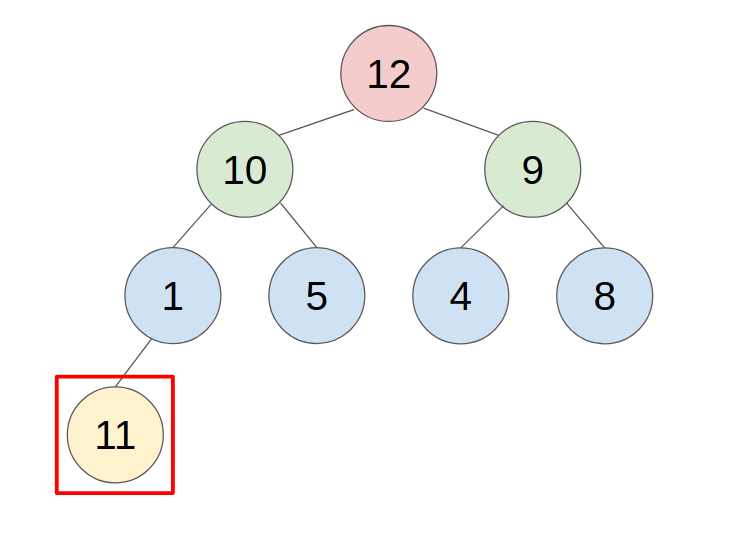
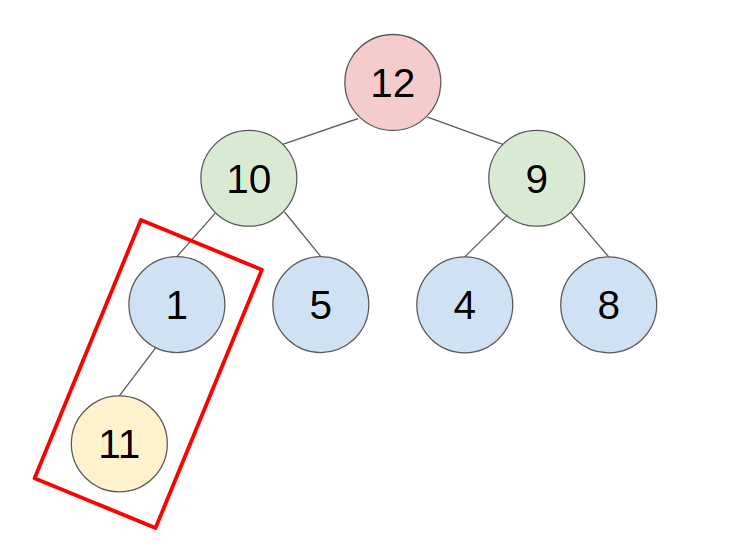
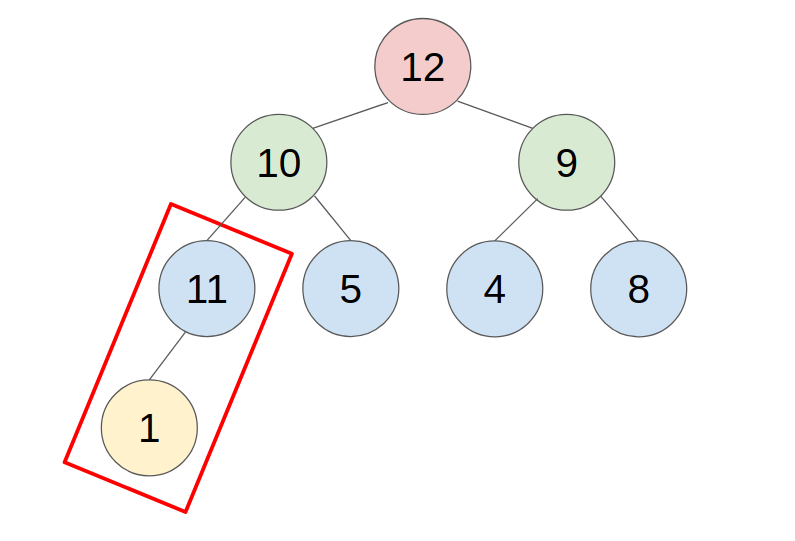
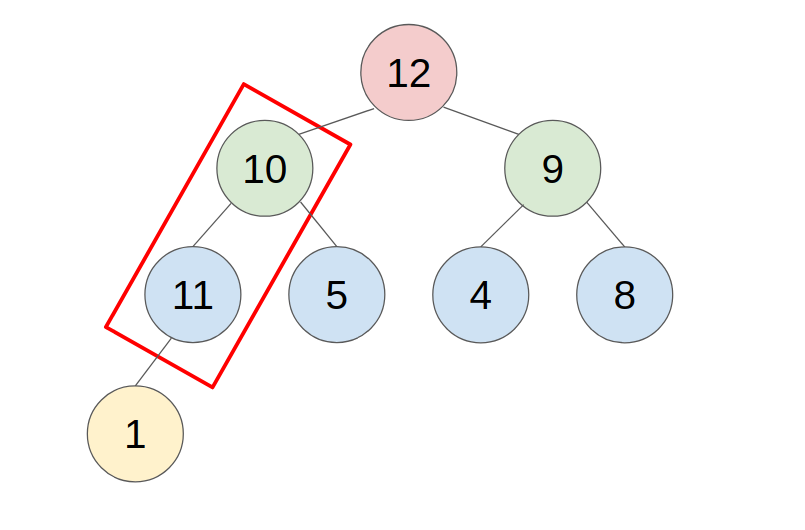
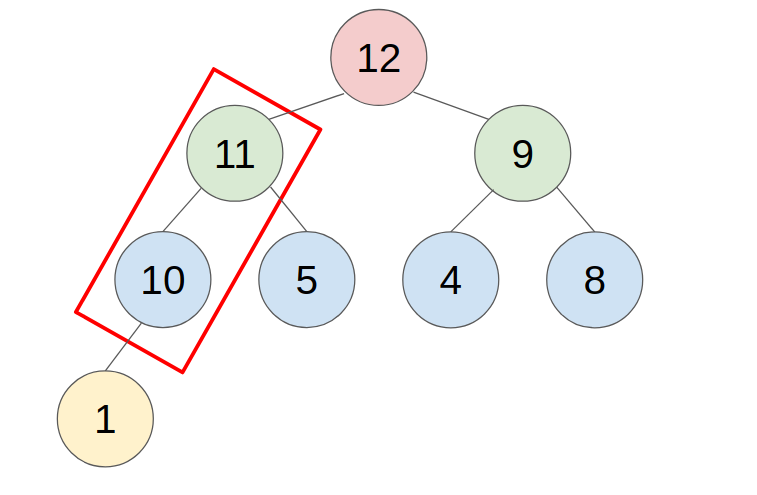
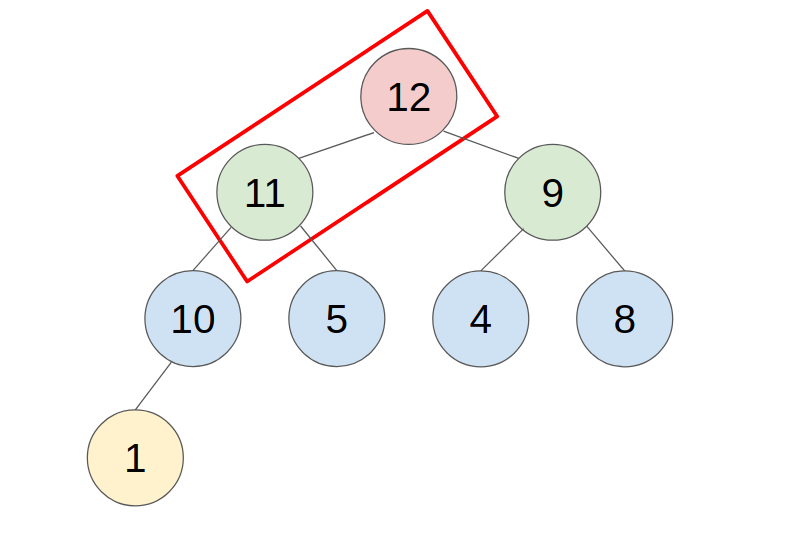
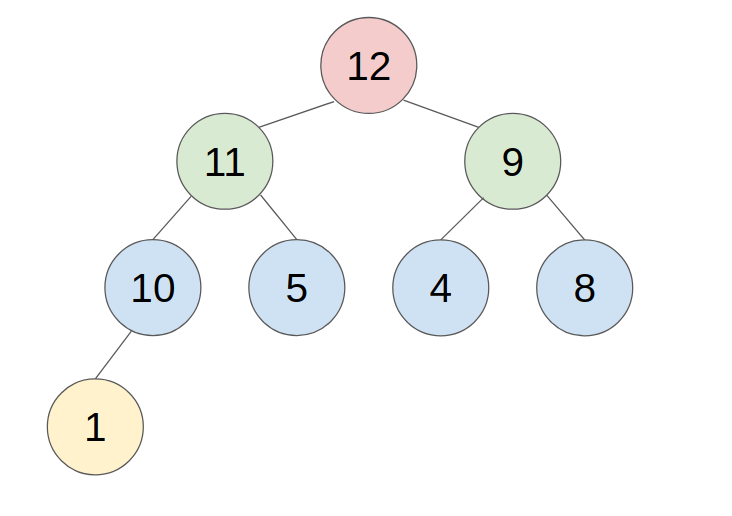
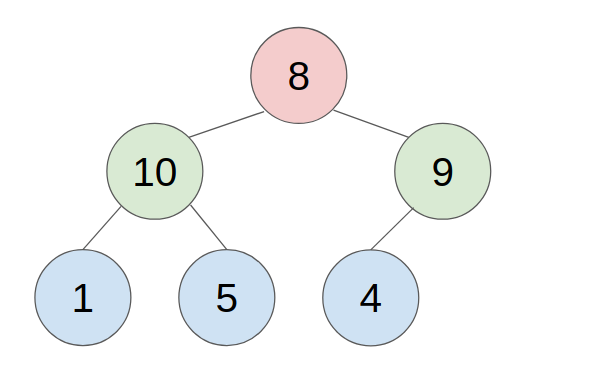
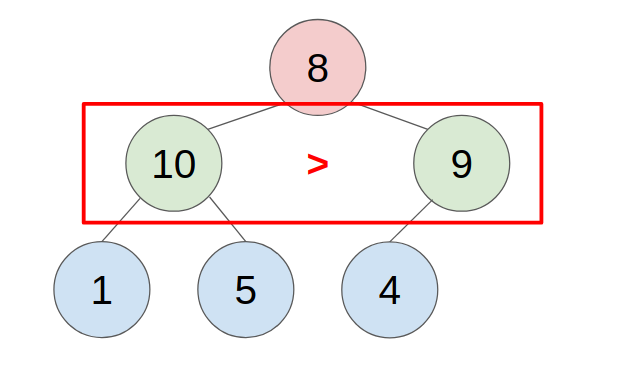
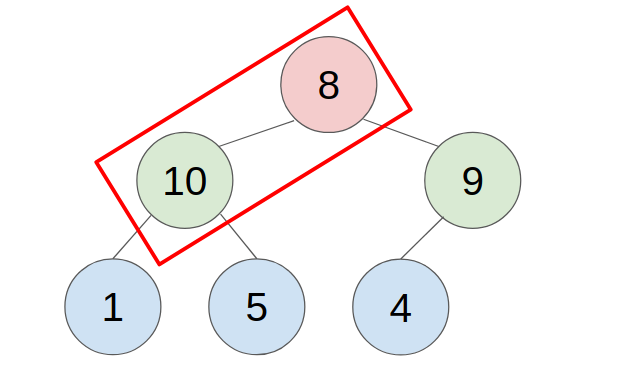
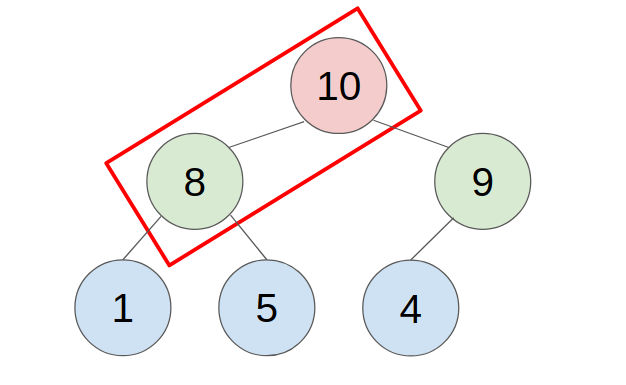
2. POP
- put the last element to the top(root) of the heap.
- compare with the greater child, swap them until all child is smaller than it.
- example:
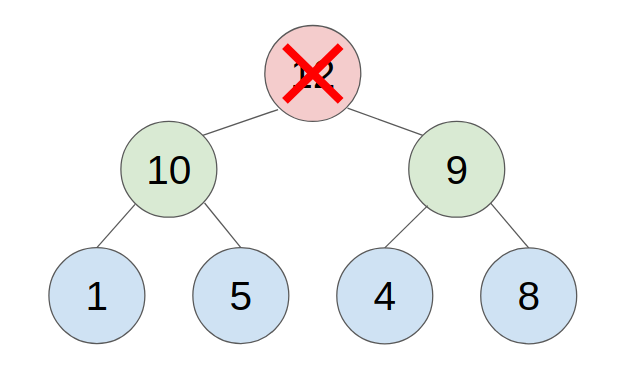
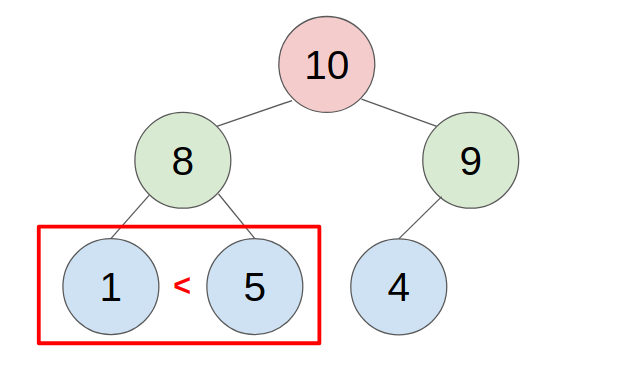
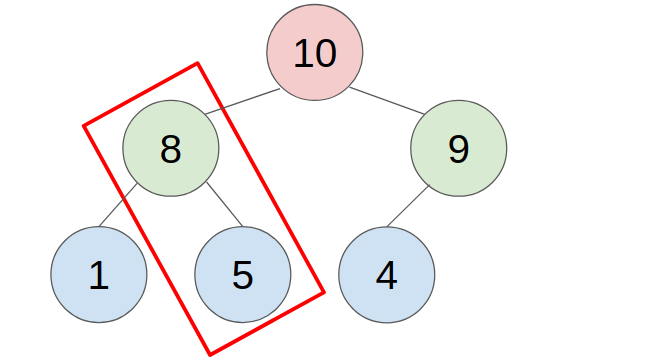
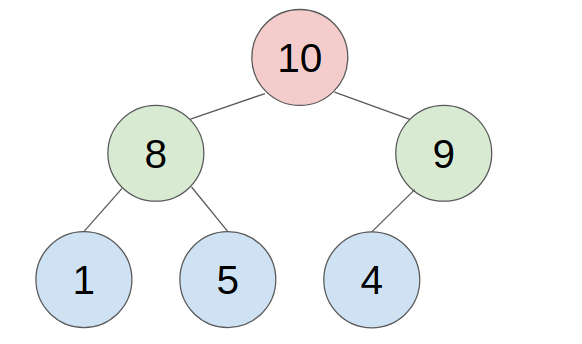
REQUIREMENTS:
Implement the constructor, push(), max(), pop() member functions of both the Array_MAX_HEAP and List_MAX_HEAP classes and deleteTree() of List_MAX_HEAP class.
Hint
For easy to solve this problem, you can call findparent(int cnt, ListNode *root) to return a ListNode which is the parent of node[cnt] in List_MAX_HEAP class.
Input
The first line contains an integer n.
Each of the next n lines has an instruction.
The instruction will be either:
- A_push: push a new element ai into the array_max_heap.
- L_push: push a new element ai into the list_max_heap.
- max: show the max element. if the max-heap is empty, print -1.
- A_pop: show and pop the max element in the array_max_heap. if the max-heap is empty, print -1.
- L_pop: show and pop the max element in the list_max_heap. if the max-heap is empty, print -1.
- size: show the size of the heap.
For all testcase:
1 <= n <= 1000, 0 <= ai < 231
(2/6) only A_push, L_push or size instruction
(2/6) only A_push, L_push, size or max instruction
(2/6) contains all instruction
Output
For max, A_pop or L_pop instruction, print the max element in the heap.
For size instruction, print the size of the heap.
Remember to print \n at the end of output.
Sample Input Download
Sample Output Download
Partial Judge Code
13131.cppPartial Judge Header
13131.hTags
Discuss
Description
You will be given a preordered polynomial f(x). There will be Q queries, for each query x, please calculate the answer of f(x).
This is a partial judge problem, we have already implement a class Function to you. class Function has two functions:
- static Funtion *parse(stringstream &ss):
used to parse the input, and it's already implemented. - double eval(double x):
used to calculate f(x), and this needs all its derived class to override it.
You need to implement the following 6 class inheritted from Function:
- Constant: represent a constant value, ex. 1, 5.3 etc.
- static Constant *create(double x):
read a double x as the constant
- static Constant *create(double x):
- Variable: represent variable, in this problem, the only variable is x.
- static Variable *create(string s):
read a string s as the variable
- static Variable *create(string s):
- Polynomial: represent polynomial(xn), ex. 53, x7, 9x.
- static Polynomial *create(Function *a, Function *b):
read Function *a and Function *b as the base and exponential of the polynomial, which represent ab
- static Polynomial *create(Function *a, Function *b):
- Arithmetic: represent a arithmetic formula, ex. 5 + 3, 7 * x, x / 2.
- static Arithmetic *create(Function *a, char op, Function *b):
read Function *a, char op, and Function *b, the char op contains '+', '-', '*', '/'
- static Arithmetic *create(Function *a, char op, Function *b):
- Sin: represent a sine function sin(f(x)).
- static Sin *create(Function *a):
read Function *a, represents sin(a)
- static Sin *create(Function *a):
- Cos: represent a cosine function cos(f(x)).
- static Cos *create(Function *a):
read Function *a, represents cos(a)
- static Cos *create(Function *a):
Please paste the following code after the code you write, and don't forget to include "function.h"!
Function* Function::parse(stringstream &ss){
string s;
ss >> s;
if(s == "+" || s == "-" || s == "*" || s == "/"){
Function *a = parse(ss), *b = parse(ss);
Function *now = Arithmetic::create(a, s[0], b);
return now;
}else if(s[0] == 'x'){
Function *now = Variable::create(s);
return now;
}else if(s == "**"){
Function *a = parse(ss), *b = parse(ss);
Function *now = Polynomial::create(a, b);
return now;
}else if(s == "sin"){
Function *a = parse(ss);
Function *now = Sin::create(a);
return now;
}else if(s == "cos"){
Function *a = parse(ss);
Function *now = Cos::create(a);
return now;
}else{
Function *now = Constant::create(atoi(s.c_str()));
return now;
}
}
Input
The first line contains a preordered polynomial f(x):
- Constants and Variable: constant value or variable x, ex. x, 5.3, 7
- Polynomial operator: ** a b, represent ab
- Arithmetic operator: op a b, represent a op b, ex. + 5 x means 5 + x. op constains only + - * /
- Trignomotric operator: op a, represent op(a), ex. sin x means sin(x). op contains only sin and cos
The second line contains an integer Q, means the number of queries.
The following Q lines are the queries, each line contains a number x.
The length of the first line won't exceed 1e6, and 1 <= Q <= 2e5.
Each constant and query is between [-100, 100]. It's guarantee that no overflow and divided by 0
Output
For each x, please output the answer of f(x).
Sample Input Download
Sample Output Download
Partial Judge Code
13890.cppPartial Judge Header
13890.hTags
Discuss
Description
In computer programming, a naming convention is a set of rules for choosing the character sequence to be used for identifiers which denote variables, types, functions, and other entities in source code and documentation, with the goal of enhancing program readability.
For the naming of identifiers, a common recommendation is "Use meaningful identifiers." A single word may not be as meaningful, or specific, as multiple words. Consequently, some naming conventions specify rules for the treatment of "compound" identifiers containing more than one word. Three most popular naming conventions are explained below:
- kebab case is a naming convention where words are separated by hyphens (“-”). For example, my-variable-name or my-function-name are examples of the kebab case.
- snake case is a naming convention where words are separated by underscores (“_”). For example, my_variable_name or my_function_name are examples of the snake case.
- camel case is a naming convention where the first letter of each word is capitalized and there are no separators. For example, MyVariableName or MyFunctionName are examples of the camel case.
(From Wikipedia, the free encyclopedia, https://en.wikipedia.org/wiki/Naming_convention_(programming))
In this problem, we consider an Integrated Development Environment (IDE) that supports naming convention conversion. We assume that the kebab case is the default naming convention. The IDE can convert to a different naming convention according to a programmer's preference. The IDE can also revert back to the default naming convention for the integration among multiple program files.
We first design the abstract base class ‘Case’ as an interface, which contains two pure virtual member functions:
- convert: convert to the desired naming convention;
- revert: revert back to the default naming convention, i.e., the kebab case.
#include <iostream>
#include <string>
using namespace std;
class Case{
protected:
bool converted;
string name;
public:
virtual void convert() = 0;
virtual void revert() = 0;
virtual ~Case(){}
Case(string s): converted(false), name(s){}
void show(ostream &os){
os << name;
}
bool is_converted() const{
return converted;
}
};
class SnakeCase : public Case{
public:
SnakeCase(string s): Case(s){}
void convert(){
converted = true;
for(int i = 0; i < name.length(); i++){
if(name[i] == '-') name[i] = '_';
}
}
void revert(){
converted = false;
for(int i = 0; i < name.length(); i++){
if(name[i] == '_') name[i] = '-';
}
}
};
class CamelCase : public Case{
public:
CamelCase(string s): Case(s){}
void convert();
void revert();
};
In ‘function.h’, we also add the class ‘SnakeCase’ as a sample of implementing a derived class of the base class ‘Case’.
You are asked to implement another derived class ‘CamelCase’ by overriding the two virtual functions, convert and revert.
Note
It is highly recommended to practice std::stringstream in this problem. Here is a simple code that shows you how to use stringstream:
#include <iostream>
#include <sstream> // header file for stringstream
using namespace std;
int main(){
string s;
stringstream ss;
getline(cin, s);
ss << s;
while(!ss.eof()){
string t;
getline(ss, t, ' ');
cout << t << "\n";
}
return 0;
}
/*
- Sample Input
This is a sentence for testing this code.
- Sample Output
This
is
a
sentence
for
testing
this
code.
*/
For more information, please refer to this article.
Input
A line contains only lowercase letters and hyphens.
Output
The Snake case and the Camel case for the input string. Please refer to the sample output for details.
Sample Input Download
Sample Output Download
Partial Judge Code
13891.cppPartial Judge Header
13891.hTags
Discuss
Description
Mixed nuts, especially peanuts, has always been Anya's favorite snack. They come in various shapes and sizes: cubes, cuboids, spheres, cones, and cylinders, each with their own unique taste and texture.

However, Anya got poor grades in her math class, and she struggles to acquire the Stella Stars needed for Loid's secret mission -- to get closer to Donovan Desmond and uncover his scheme.

To help Anya on her schoolwork, Loid decided to teach her the basics of geometry with the shapes of mixed nuts. Given several nuts of different shapes and sizes, Loid wants Anya to calculate total volume of the nuts. Since Anya has the ability to read other people's minds, she can easily read the volume formula for each shape straight from Loid's mind. However, she is not familiar with the calculations, so she needs your help to build a program that can calculate the volume of the nuts.
The volume of a nut can be calculated using the following formulas:
- Cube: $V = s^3$, where $s$ is the side length of the cube.
- Cuboid: $V = l \times w \times h$, where $l$, $w$, and $h$ are the length, width, and height of the cuboid, respectively.
- Sphere: $V = \frac{4}{3} \pi r^3$, where $r$ is the radius of the sphere.
- Cone: $V = \frac{1}{3} \pi r^2 h$, where $r$ is the radius of the base, and $h$ is the height of the cone.
- Cylinder: $V = \pi r^2 h$, where $r$ is the radius of the base, and $h$ is the height of the cylinder.
Given a base class Nut, implement the derived classes CubeNut, CuboidNut, SphereNut, ConeNut, and CylinderNut that represent the shapes of mixed nuts. You should use setVolume to set the corresponding volume of each nut on construction.
Hints
- Be careful that the type of volume is double, and
4/3=1is of typeint. - You only need to implement the constructor of each derived class.
- Note that
CubeNutinherits fromCuboidNutinstead ofNut. - Use
oj::Nut::PIas your $\pi$ in the calculation.
Input
This is a partial judge problem, input and output are handled by main.cpp.
For each line of input, you will be given a string shape, followed by the corresponding parameters for the shape. The parameters are separated by a single space, and the order of the parameters is as follows:
- Cube: $s$ (side length)
- Cuboid: $l , w , h$ (length, width, height)
- Sphere: $r$ (radius)
- Cone: $r , h$ (radius, height)
- Cylinder: $r , h$ (radius, height)
You should do some basic check: if the input is illegal (e.g. length < 0), then the volume should be 0. Also, you need to consider the scenario like Cuboid -1 -2 3, where volume would be 0 instead of 6.
Constraints
- $\text{|s|, |l|, |w|, |h|, |r|} \leq 1000$
- $\text{s, l, w, h, r}$ are presented in decimal format with at most 4 decimal places.
- $0 \leq \text{# of shapes} \leq 1000$
- Result is within the range of
double.
Output
This is a partial judge problem, input and output are handled by main.cpp.
Output the total volume of the nuts, rounded to 4 decimal places.