| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10998 | Stack |
|
| 11443 | 3DShape |
|
| 13520 | Dynamic Array |
|
| 14604 | Big Orange Cat's Polynomial I |
|
Description
A stack is an abstract data type that serves as a collection of elements, where a node can be added to a stack and removed from a stack only at its top. Two principal operations can be used to manipulate a stack: push, which adds an element at the top, and pop, which removes the element at the top of the collection.
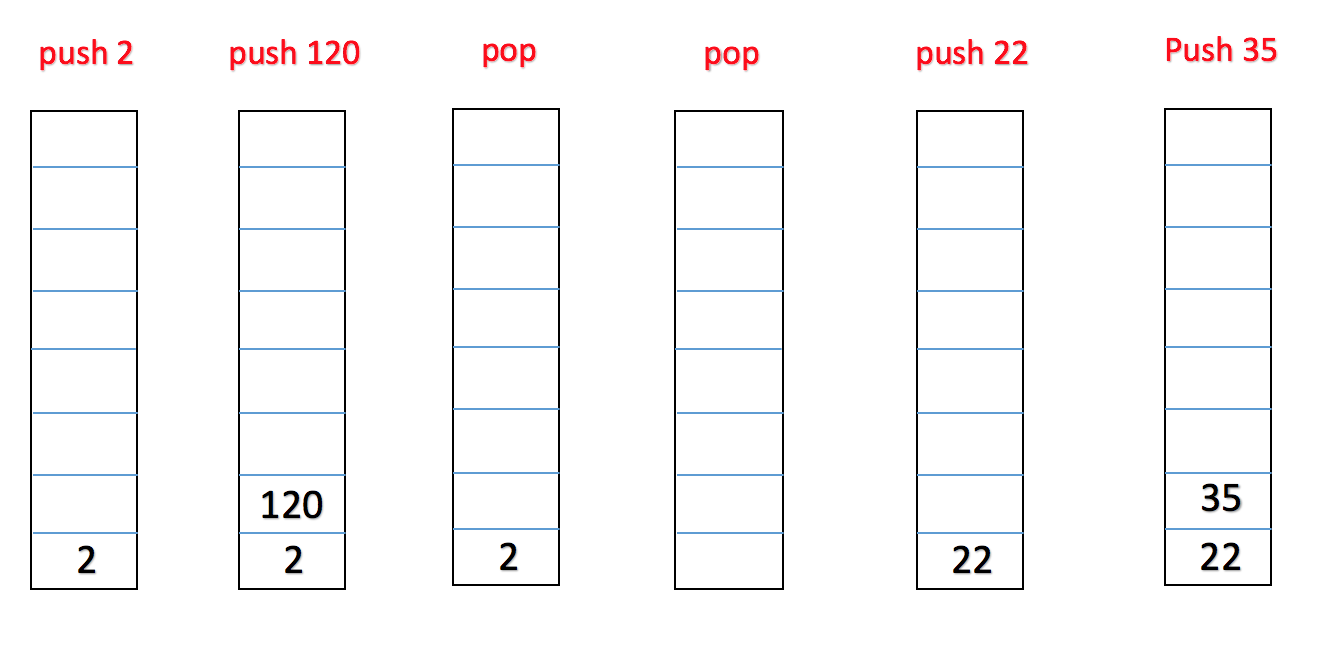
Let’s see how the stack data structure can be realized in C++.We have an approach to implement stack: linked list. Thus, we define a class as follows:
class List_stack {
public:
List_stack();
~List_stack();
void push(const int &);
void pop();
void print();
private:
ListNode *head;
ListNode *tail;
};
where List_stack implements the stack data structure
REQUIREMENTS:
Implement the constructor, destructor, push(), pop() and print() member functions of List_stack classes.
Note:
1.This problem involves three files.
- function.h: Class definitions.
- function.cpp: Member-function definitions.
- main.cpp: A driver program to test your class implementation.
You will be provided with main.cpp and function.h, and asked to implement function.cpp.
function.h
main.cpp
2.For OJ submission:
Step 1. Submit only your function.cpp into the submission block.
Step 2. Check the results and debug your program if necessary.
Input
There are three kinds of commands:
- “push integerA” represents adding an element with int value A at the top of the stack.
- “pop “ represents removing the element at the top of the stack.
- “print” represents showing the current content of the stack.
Each command is followed by a new line character.
Input terminated by EOF.
Output
The output should consist of the current state of the stack.
When the stack is empty, you don’t need to print anything except a new line character.
Sample Input Download
Sample Output Download
Partial Judge Code
10998.cppPartial Judge Header
10998.hTags
Discuss
Description
Warning: You are not allowed to use malloc and free
Giving a bass-class Shape3D and 4 derived class : Sphere (球體), Cone (圓錐), Cuboid (長方體), Cube (立方體)
You need to calculate the volume of each shape.
PS:
V of Sphere: V = 4/3 π r3
V of Cone: V = 1/3 π r2 h

note : Remember to do some basic check, if the input is illegal (e.g. length < 0, pi < 0 .....) then the volume should be 0.
You don't need to consider the scenario like Cuboid -1 -2 3, volume would be 0 instead of 6.
Hint1: Be careful the type of volume is double. 4/3=1 (int), so it should be 4.0/3.0
Hint2: You only need to implement the constructors.
Hint3: Note that Cube inherited Cuboid not Shape3D.
Input
There are only 4 shapes in this problem :
- Sphere, following by its radius and pi. (e.g. Sphere 30 3.14)
- Cone, following by its radius of bottom plane, height and pi. (e.g. Cone 3 100 3.14)
- Cuboid, following by its length, width and height. (e.g. Cuboid 2 3 7)
- Cube, following by its length. (e.g. Cube 2)
Output
Ouput the total volume of all the shapes.
Sample Input Download
Sample Output Download
Partial Judge Code
11443.cppPartial Judge Header
11443.hTags
Discuss
Description
Array vs. Linked List
Array is a basic and fundamental concept in C/C++. It is a series of data which is arranged continiously in the memory space and can be accessed by index. Array is fast for indexing (using the given index to access the certain data), because the memory address of the destination can be calculated quickly. However, the capacity of the array is fixed after the declaration.
In I2PI (introduction of programming 1), we introduce a data structure called "linked list" which supports appending and deleting elements dynamically. The elements are stored in a series of "nodes", where each node points to the address of the next node. It is fast at appending elements but slow at indexing. To access the item of index i, you need to move i steps from head to obtain it.
Dynamic Array
In this problem, we will introduce a new data structure called "dynamic array" (abbreviated to "Darray" in the following statement) which supports dynamic capacity and indexing. We targeted to a simple Darray which has the following three variables
- size : the number of elements stored in the array
- capacity : the maximum number of elements which can be stored in the array
- *data : the pointer which stores the address of the array
and two operations
- pushback: append an element to the back
- indexing : access the data by the given index.
To understand the concept of size and capacity, consider an array declaration:
// or
int *data = new int[5];
At first, the capacity is 5, but the size is 0 because no data is stored inside the array. Next, we push 5 elements to the array:
the capacity is still 5 but the size changes from 0 to 5. Therefore, no element can be appended to the array.
If we still want to append additional elements, we'll allocate a new array space with the double capacity and copy the data from old array to the new one. Note that the old array should be freed to avoid memory leak.
In this case, the capacity becomes 10 and the size is 6.
Implementation
You should implement the following functions based on the description above:
- int& operator[](int): access data like using array. Users and main.cpp should/will not access the index which is greater or equal to size.
- void pushback(int x): append the element x
- void clear(void): clear the array (set size to 0) so that the next pushbacks will place elements in data[0],data[1] and so on.
- int length(void): return the current size.
- void resize(void): double the capacity and copy the data.
- ~Darray(): destructor
Note that main.cpp acts like a functional tester for your Darray. There's no need to understand it. You should test your Darray by yourself.
class Darray {
public:
Darray() {
capacity = 100;
size = 0;
data = new int[capacity];
};
~Darray();
int& operator[](int);
void pushback(int x);
void clear(void);
int length(void);
private:
void resize(void); // double the capacity
int *data;
int capacity;
int size;
};
Darray arr;
for (int i = 0; i < 5; i++) arr.pushback(i*i);
arr[2] += 100 + arr[3];
for (int i = 0; i < arr.length(); i++)
cout << arr[2] << ' '; // Print: 0 1 113 9 16
cout << endl << arr.length() << endl; // Print: 5
arr.clear();
cout << arr.length() << endl; // Print: 0
arr.pushback(9487);
cout << arr.length() << ' ' << arr[0] << endl; // Print: 1 9487
More Notes: Time Complexity of Dynamic Array
Although it seems that copying the whole array will make dynamic array slow, we will analyze the time complexity to show that dynamic array is fast. Recall what Big-O Notation is where we introduced it in "The Josephus problem". O(2n+100)=O(2n)=O(n) means that the operation takes about n steps while O(2)=O(1) takes "constant" time. For array operations, we wish to have O(1) of indexing and pushback. In the following analysis, we will evaluate the amortized time complexity, which can be comprehended as calculating the average time complexity instead of the complexity of total operations. Amortized time complexity = (complexity of total operations) / (number of operations).
Suppose that C0 is the initial capacity and n is the number of operation of pushback. We discuss the time complexity in several cases:
- Expand 0 time, n <= C0.
Since there's no expand operation, the total time complexity is O(1)*n=O(n). The amortized time complexity is O(n)/n=O(1). - Expand 1 time, C0 < n <= C1, C1 = 2*C0.
Push C0 items to array: O(C0)
Expand and copy: O(C0), since there're C0 elements to be copied.
Push n-C0 items to array: O(n-C0)
The total time complexity is O(C0)+O(C0)+O(n-C0) = O(n+C0). Since C0 < n <= C1, O(2C0) < total time complexity <= O(3C0). The amortized time complexity ranges in [O(3/2), O(2)). We identify it by the upper bound : O(2). - Expand 2 times, C1 < n <= C2, C2 = 2*C1.
The amortized time complexity should be O(3). You can verify it by your own.
From the above analysis, if it expand i times, the amortized time complexity for appending an element is O(i+1). However, i won't be very large because the capacity grows exponentially so that we often regard the complexity as O(1), or, constant time. For instance, C0=100, after expanding 20 times, the capacity will be 100*220≈108.
Input
This is handled by the main function.
Output
This is handled by the main function.
Sample Input Download
Sample Output Download
Partial Judge Code
13520.cppPartial Judge Header
13520.hTags
Discuss
Description
You are given definitions of multiple polynomials, such as F(x)=+2x^2 +3x +1 and G(x)=+2x +1 , along with several operations to perform on these polynomials, like F(2)+G(3), You need to compute the results of these operations.
This problem is a partial judge.
Please implement functions defined in the header file:
Polynomial(int deg, const int *coeffs)Constructor: Initializes polynomial with degree and coefficient arrayPolynomial(const Polynomial& other)Copy constructor: Creates a copy of another polynomialPolynomial operator+(const Polynomial& other) constAddition operator: Adds two polynomialsPolynomial operator-(const Polynomial& other) constSubtraction operator: Subtracts one polynomial from anotherPolynomial operator*(const Polynomial& other) constMultiplication operator: Multiplies two polynomialsPolynomial& operator=(const Polynomial& other)Assignment operator: Assigns one polynomial to anotherint evaluate(int x) constEvaluates polynomial at given value x, The result must be taken modulo 109+7. If the result is negative, add 109+7 after taking the modulo to ensure the final answer is non-negative.friend std::ostream& operator<<(std::ostream& os, const Polynomial& poly)Output stream operator: Prints polynomial to output stream
Input
The first line contains two positive integers n and m, where n is the number of polynomials, and m is the number of operations to perform
The next n lines describe the polynomials. Each line is in one of two formats:
<symbol> = <polynomial>, which defines the mathematical expression for that polynomial (e.g.,"F = 2x^2 + 3x + 1").<symbol1> = <symbol2>, which means the polynomial defined by<symbol1>is the same as the polynomial defined by <symbol2>.
<func1> <op> <func2> <x>, where:<func1>and<func2>are the names of two polynomials.<op>is an operator, which can be+,-, or*, indicating the operation to perform (addition, subtraction, or multiplication).<x>is the value of x to substitute into the polynomials
Constraints
- The degree of each polynomial is at most 100.
- 1 <= n <= 26
- 1 <= m <= 1000
- All coefficients and values in the polynomials are less than or equal to 105
- The symbol will only consist of a single uppercase letter.
Subtasks
- testcase 1: The operation will only involve addition (+)
- testcase 2: The operation will only involve subtraction (-)
- testcase 3: The operation will only involve multiplication (*)
- testcases 4 ~ 6: No additional restrictions
Output
<poly> = <ans>, where:-
<poly>is the mathematical expression of the resulting polynomial after performing the operation on<func1>and<func2>. -
<ans>is the value of the resulting polynomial evaluated at x = x. -
If a polynomial has a coefficient of 0, represent it as +0.
-
The result
<ans>must be taken modulo 109+7. If the result is negative, add 109+7 after taking the modulo to ensure the final answer is non-negative.