| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12680 | Card Magic |
|
| 14586 | ISTP |
|
| 14595 | Big Orange Cat's Orange Tree II |
|
Description
Mr. Lu is a famous magician. There’s a poker magic tutorial on his youtube channel.
There’re N stacks of cards on the table at begining.
And then, Mr. Lu make M actions on these card stacks.
There’s only two kinds of actions Merge and Cut:
- Merge x y: put the x-th card stack on the top of y-th card stack.
- Cut x i: cut the x-th card stack into two stacks. One is the card stack contains ( 1~i )-th cards of original stack. The other one is the remaining. The former’s index will be x, the latter’s will be (x+1)
- The indexes of stacks and cards will be changed after Merge and Cut.
For example:

As a lazy CS student, you only focus on the result.
Therefore, you decide to write a program to compute the final state of card stacks.
It’s partial judge for this problem.
Please download the code at the bottom to see the interface and main function.
You have to implement a data structure like below:

Input
Two integer N,M on the first line.
For each of the next N lines, there’re several integers Ni and Ci,1,Ci,2...Ci,Ni.
Ni means the number of cards in the i-th stack.
Ci,j denotes the j-th card of i-th stack.
The folloing M lines contains one action per line.
Every Action is one of “Merge x y” or “Cut x i”.
It’s guaranteed that:
- 1 ≤ N, M ≤ 9000
- ∑ Ni ≤ 4∗104
- Ci,j is non-negative integer.
- In “Merge x y” action:
- the x, y-th stacks always exist.
- x is not equal to y.
- In “Cut x i” action:
- the x-th stack always exists.
- i is always between 1 and Nx - 1.
- There’s at least 1 card in each card stack.
Output
Print the card stacks by the order of index.
One line for one card stack.
Please refer to the sample input/output for the precise format.
There is a ‘\n’ at the end of each line.
Sample Input Download
Sample Output Download
Partial Judge Code
12680.cPartial Judge Header
12680.hTags
Discuss
Description
ISTP is not MBTI, but the task you need to perform: Insert and Search The Parentheses tree.
You are given a binary search tree of length N represented in parentheses. The binary search tree is represented according to the following rule:
If a node is NULL, represent it as ()
Next, you will perform T insertion operations. Each operation involves inserting a node with value A. The insertion rule is as follows:
Starting from the root node, if A is less than the current node's value, move to the left subtree. If A is greater than the current node's value, move to the right subtree, until an NULL node is found. Insert a node with the value A at that NULL node.
Your task is to perform T insertion or search operations:
- insert A: Starting from the root node, if A is less than the current node's value, move to the left subtree. If A is greater than the current node's value, move to the right subtree, until an NULL node is found. Insert a node with the value A at that NULL node.
- search B: Find the node with the B-th largest value in the tree and return its value. B is guaranteed to be between 1 and the total number of nodes in the tree.
Finally, output the binary tree after completing the operations, expressed in parentheses.
For sample input:
3(2(1()())())(4()())
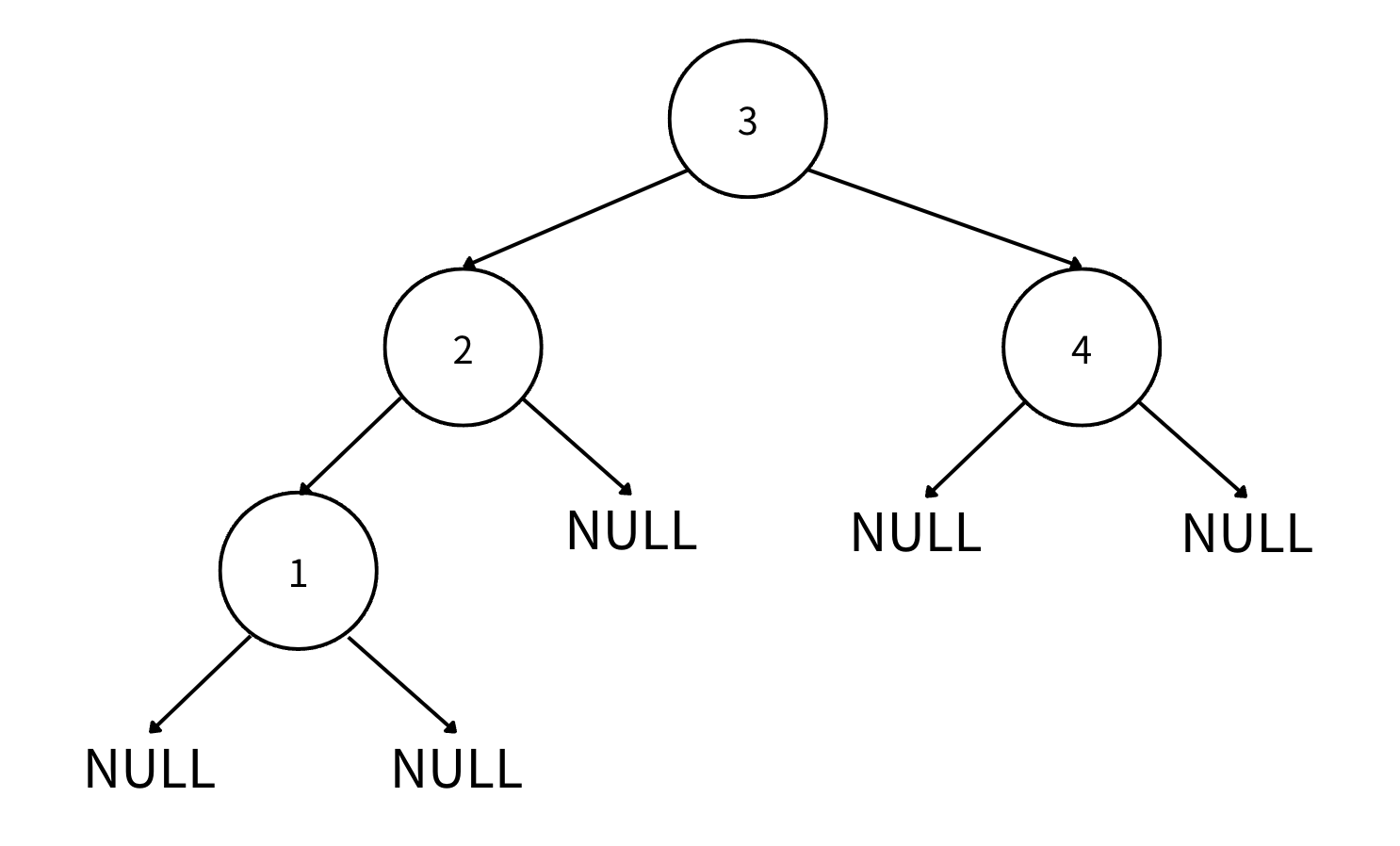
The Parentheses tree is guaranteed to satisfy the following condition before and after all T operations:
- As a binary search tree, it ensures each node's left child is less than the node and its right child is greater.
- All node values in the tree are unique.
This question is a partial judge.
Please implement functions defined in the header file.
- insert: Insert a node with value A into the parentheses tree.
- search: Find the node with the B-th largest value in the tree and print its value.
Input
The first line contains an integer N, representing the length of the string expression of the parentheses tree.
The second line contains a parentheses expression of length N.
The third line contains an integer T, representing the number of insertion / search operations to perform.
The following T lines each contain either an insert A operation or a search B operation.
Constraints
- 0 ≤ N ≤ 106
- 1 ≤ T ≤ 1000
- -109 ≤ D, A ≤ 109
- 1 ≤ B ≤ all nodes in the tree
Subtask
- Testcases 1 ~ 3: insertion operation
- Testcases 4 ~ 6: No additional restrictions
Output
Output the binary tree after completing the operations, expressed in parentheses.
Sample Input Download
Sample Output Download
Partial Judge Code
14586.cPartial Judge Header
14586.hTags
Discuss
Description
Big Orange Cat (大橘) found a strange orange tree in his backyard, represented as a syntax tree with n nodes. Each node is either a number or an operator, including basic operators (+, -, *) and m custom operators.
Each custom operator (the i-th one) is defined as follows:
- oi: the symbol representing the operator.
- ki: the number of input parameters (child nodes) it accepts.
- si: the preorder traversal of the syntax tree defining its computation rule, consisting of +, -, *, numbers, and operators defined earlier. In other words, the syntax tree of a custom operator may include other previously defined operators; please refer to Example 6.
In the syntax tree, parameters are denoted as A (first parameter), B (second parameter), and so forth. For example:
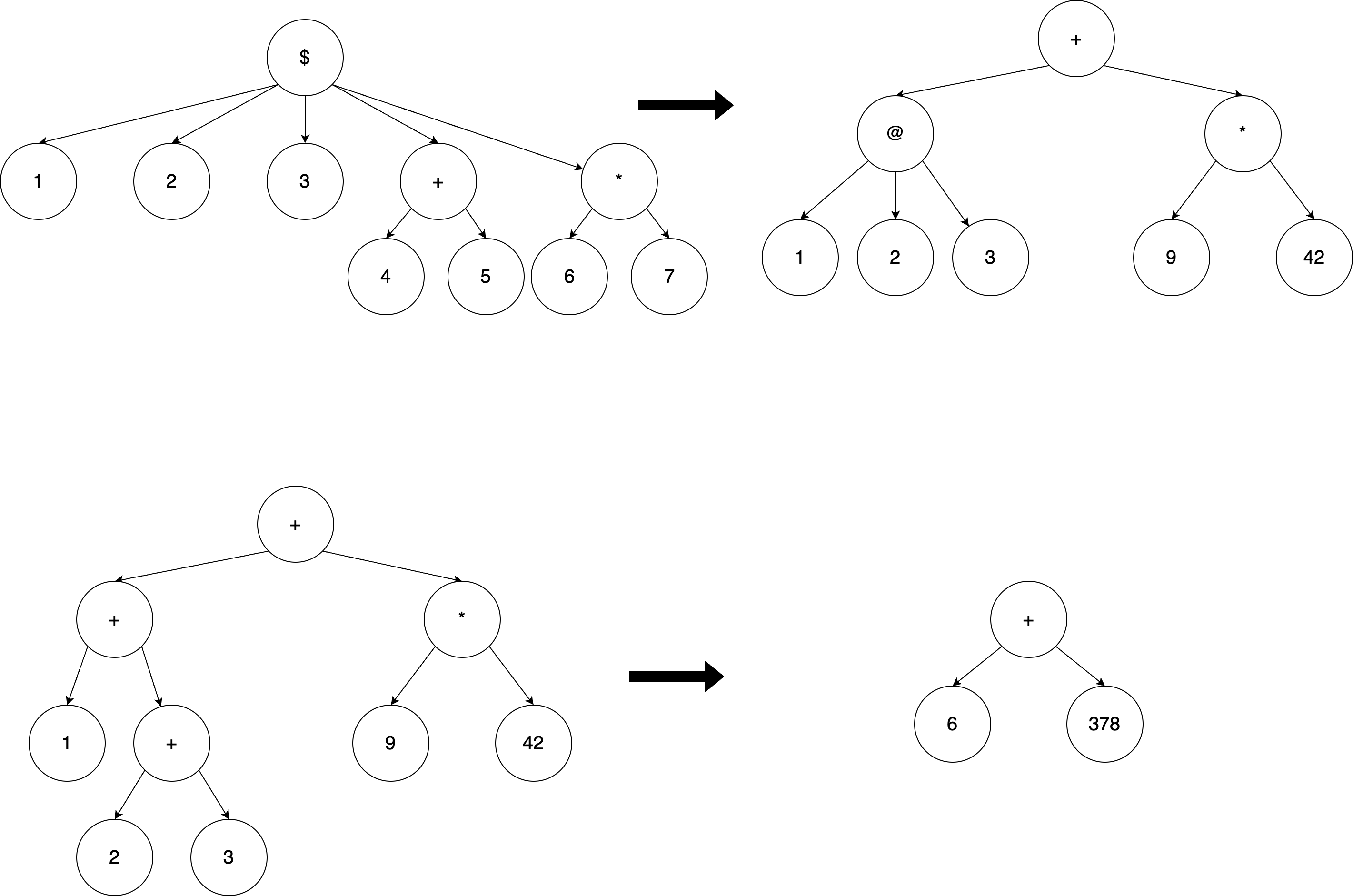
Explanation of Sample Test Case 6:
In this case, the custom operator @(A, B, C) computes A + B + C, represented by the preorder traversal + A + B C, and the other custom operator $(A, B, C, D, E) computes @(A, B, C) + (D * E), represented by the preorder traversal + @ A B C * D E
Given the expression 1 2 3 + 4 5 * 6 7, where A = 1, B = 2, C = 3, D = 4 + 5, E = 6 * 7,we break down $ and obtain the syntax tree + @ 1 2 3 + 4 5 * 6 7. Then, we break down @ and get + @ 1 2 3 * 9 42. Finally, we compute the result as 6 + 378 = 384.
The syntax tree can be visualized as:
Next, there are q operations, and each operation can be one of the following:
- Given index, change the value or symbol of a node at positions index in the initial syntax tree’s preorder traversal.
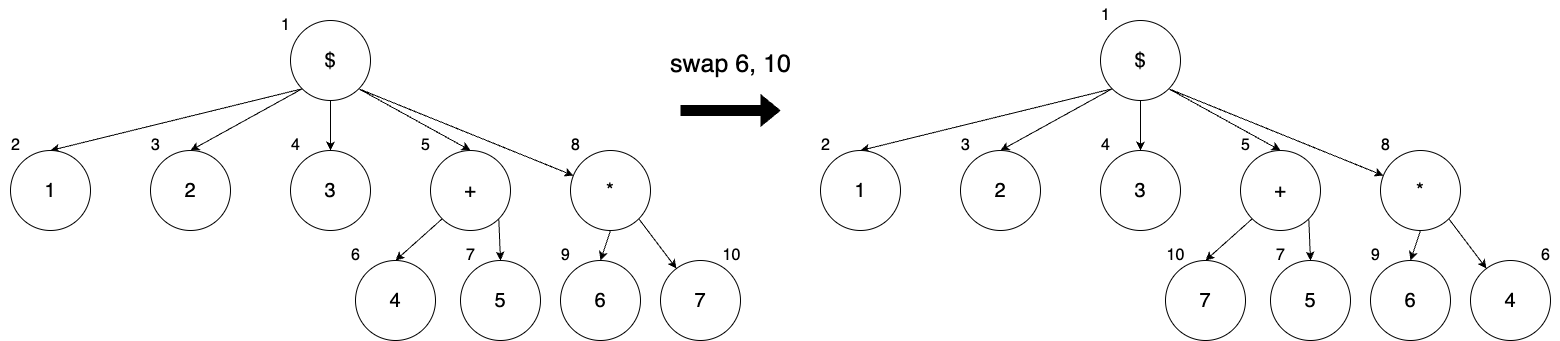
- Given index1 and index2, swap the subtrees of the nodes at positions index1 and index2 in the initial syntax tree’s preorder traversal. Note that after swapping the two nodes, their indices will also be swapped. Refer to the diagram below for clarification.
- Output the result of the syntax tree after calculation.
Input
The first line contains three integers: n, m, and q, which represent the total number of nodes, the number of custom operators, and the number of operations, respectively.
The next m lines describe the custom operators. Each line includes:
- A character oi: the symbol of the i-th custom operator.
- A positive integer ki: the number of input parameters it takes.
- A string si: the preorder traversal result of the syntax tree created by this operator’s rule, made up of numbers and operators (including +, -, *, and operators defined earlier.), with each operator or number separated by a space.
Next line contains a string representing the syntax tree’s preorder traversal result, with each element separated by a space.
The following q lines represent q operations, where each operation can be one of these:
1 index num: Change the number of the node at position index to num.2 index1 index2: Swap the subtrees of the nodes at positions index1 and index2.3: Output the result of the current syntax tree after calculation, modulo 109 + 7.
Constraints
- 1 <= n <= 104
- 0 <= m <= 10
- 1 <= q <= 105
- t and si are made up of numbers and visible characters, and si will contain other custom operators defined earlier.
- 1 <= | si | <= 150
- oi will be a visible character other than
+, -, or* - All numbers are between [0, 109].
- 2 <= ki <= 5
- The number of type 3 operations (output results) is <= 100.
- In the third type of operation, the parents of the two nodes will be different, and the two nodes being swapped will have the same properties (both are numbers, or both are operators that take the same number of parameters).
Subtasks
- testcase 1: m = 0, q = 1, ki = 2, and only the third operation is present.
- testcase 2: m = 0, ki = 2
- testcase 3: q = 1, ki = 2, and only the third operation is present.
- testcase 4 ~ 6: ki = 2
- testcase 7 ~ 8: q = 1, and only the third operation is present.
- testcases 9 ~ 10: No additional constraints.
Output
Whenever the operation 3 is encountered, output the result of the current syntax tree after calculation, modulo 109 + 7. If the result after applying 109 + 7 is negative, add 109 + 7 to it before outputting. You can refer to Example 2: the original calculation result is -69, and after adding 109 + 7, it becomes 999999938.
You can consider modifying the following code to solve this problem: