| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11832 | Play cards |
|
| 13837 | Bubbling! |
|
| 14224 | Electrical Safety |
|
| 14585 | Library Network |
|
| 14589 | Magical Apple Tree |
|
| 14590 | Decision Tree |
|
| 14592 | Inversion Count |
|
Description
Niflheimr is playing cards with his friends. As a CS student, he wants to play in a programmer way. He decides to write a program for shuffling the cards. By the way, more friends may come while he is shuffling cards, so sometimes he needs to insert new cards into the card stack, too.
Hint: You can use linked list to implement.
Input
- ADD idx num: Add a new card with number num before card idx.
- CUT a b: Move cards whose index between a and a+b-1 ( [a, a+b) ) to the top of the card stack. Order of the cards inside the moved part won't be changed.
- 1 ≤ n, m ≤ 104
- Number on cards are non-negative integer and do not exceed 107
- # of cards in the card stack will never exceeds 2*104
- in CUT operation, card with index = a+b-1 always exists.
Output
Print out the card stack from top (index 0) to buttom (largest index), each number occupies one line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
We learnt bubble sort in class, which could be implemented so easily:
void bubble_sort(int *begin, int *end)
{
for (; begin < end; end--)
for (int *ptr = begin + 1; ptr < end; ptr++)
if (*(ptr - 1) > *ptr)
iter_swap(ptr - 1, ptr);
}Short as the codes might be, it doesn't run efficiently at all. It's obvious that he number of comparisons (the if branch) would be executed \(\sum^{i=n-1}_1i\) times. In fact, we could improve the performance slightly since if inside the second for loop there's no any swap required, then the sorting is already done and no longer need to compare or swap any more.
On the other hand, the number of swaps, which equals the number of inversions, is the bottleneck of bubble sort, constraining the time complexity.
So given an array, you are to compute the two number mentioned above: minimum number of comparisons and number of swaps that bubble sort take.
Input
The first line is an integer \(n<10^4\) indicating the length of the array.
The next line contains the \(n\) integers \(a_i\in[-2^{31},2^{31})\) of the array.
Output
Please print two integers, the number of comparisons and number of swaps, separated by a space. Remember to put a '\n' at the end of line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Procat (破貓) has a lot of electrical appliances in his dormitory, such as computer, refrigerator, and electric fan. He wants to connect all the appliances to the power outlet. There is only one power outlet in his dormitory, so he needs to use extension cords and power strips to connect all the appliances to the power outlet.

Extension cords and power strips Procat currently using don't have overcurrent protection. As a friend of Procat, you are very concerned about electrical safety. You want to help Procat to connect all the appliances to the power outlet in a safe way. Luckily, you have some spare power strips with overcurrent protection. But you don't have any spare extension cords.
Power strips you have got one input and two outputs. Power strips can connect to extension cords, but power strips cannot directly connected to each other.
The price of the high-quality extension cord you want to buy is proportional to the current flowing through it. You wants to minimize the total price of the extension cords you needs to buy.
Calculate total price of the extension cords you need to connect all the appliances to the power outlet.
- After connecting all the appliances to the power outlet, it should look like a binary tree. The power outlet is the root of the tree, and the appliances are the leaves of the tree. The power strips are the internal nodes of the tree. The extension cords are the edges of the tree.
Sample
Following figures show examples of optimal ways to connect the appliances to the power outlet in each sample testcase. In each figure, squares represent power strips, circles represent appliances, and edges represent extension cords. The total price of the extension cords is the sum of current flowing through all the edges.
Sample testcase 1:
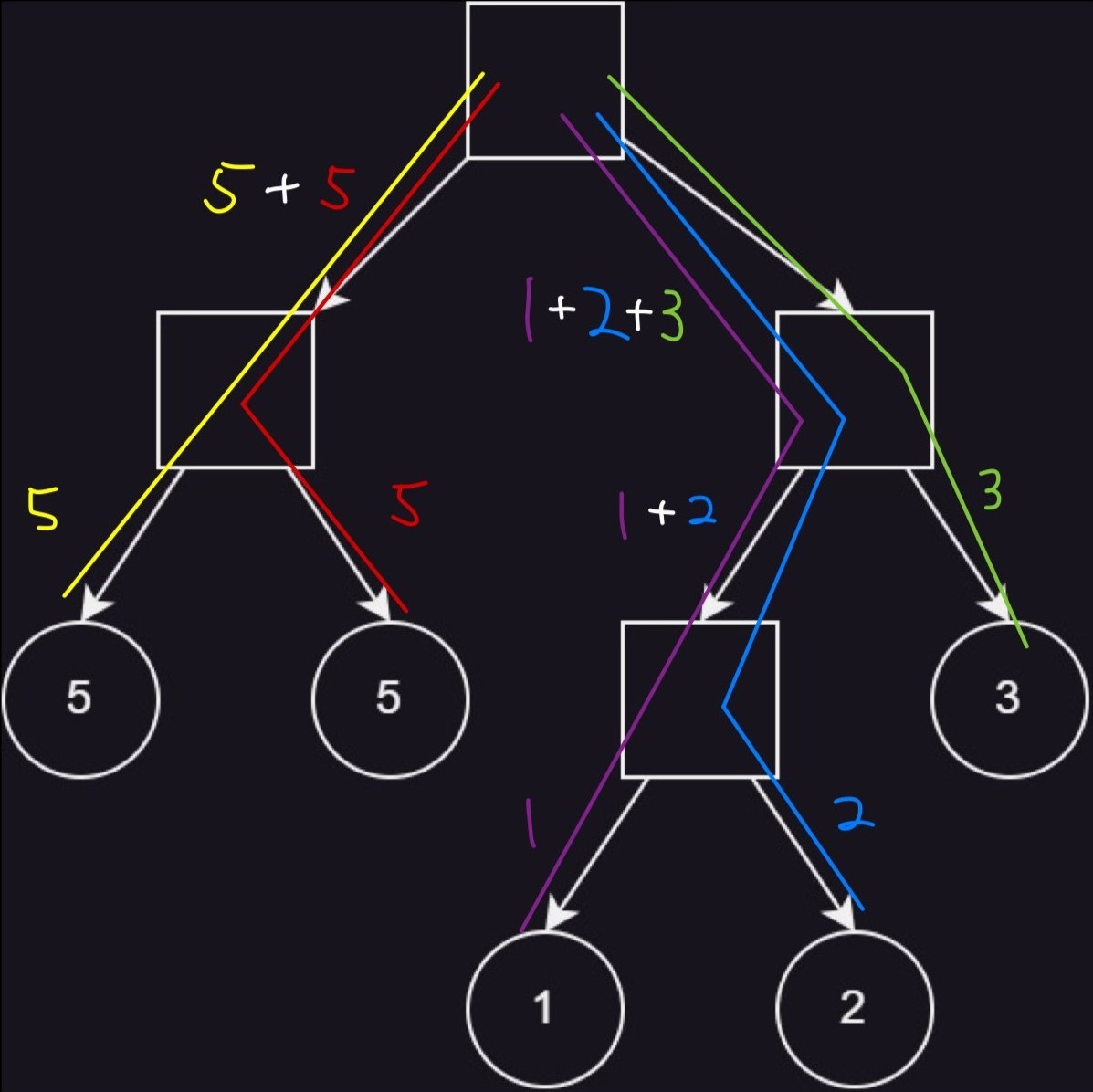
Sample testcase 2:
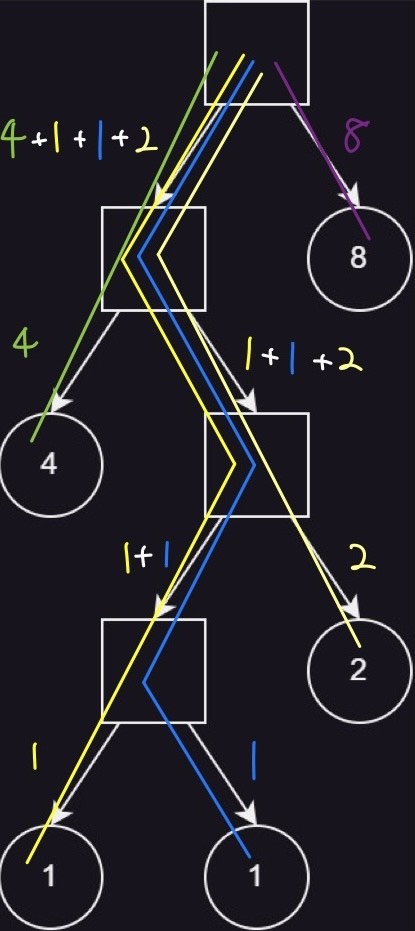
- Hint: Huffman Coding
Input
First line contains an integer \(N\), the number of electrical appliances Procat wants to connect to the power outlet.
The second line contains \(N\) integers \(a_1, a_2, \dots, a_N\), the power consumption of the \(N\) electrical appliances.
\(N\)
\(a_1 \quad a_2 \quad \dots \quad a_N\)
Constraints
- \(1 \leq N \leq 10^4\)
- \(1 \leq a_i \leq 10^9\)
Output
Output contains one line, the minimum total price of the extension cords Procat needs to buy. You don't need to output a newline at the end of the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In a remote country, there exists a unique network of libraries connected by roads. The network has some special characteristics:
- Between any two libraries, there exists exactly one path
- The roads never form loops or circles
The country's Ministry of Education wants to optimize their book-sharing system across these libraries. To optimize this system, they wants to know, for each library, the sum of the distances from the library to all other libraries. This information will help them place the most frequently accessed books in the most accessible locations (those with smaller total distances), while rarely requested books can be stored in the libraries far from the center (those with larger total distances).
Your task is help them find the distances.
Input
The first input line contains an integer n: the number of libraries. The libraries are numbered from $1$ to $n$
Then there are $n-1$ lines describing the roads that connects two libraries. Each line contains two integers $a_i$ and $b_i$: there is an road connecting library $a_i$ and $b_i$.
Constraints
- $1 \leq n \leq 2 \cdot 10^5$
- $1 \leq a_i, b_i \leq n$
Subtask
- (Testcases 1-6): $n \leq 3 \cdot 10^3$
- (Testcases 7-10): $n \leq 2 \cdot 10^5$
Output
Print $n$ integers: for each library 1, 2, $\ldots$ , $n$, the sum of the distances.
Noted that you should output one single line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Thanksone is a CS student who likes to eat apple very much so he plants a magical apple tree. We can view the magical apple tree as a tree with $N$ nodes and the root is $R$. Initially, there would be some apples on each of the nodes. Then, during the following $M$ days, one of the two things might happen on the $ith$ day:
- $k_i$ apples would grow on node $x_i$.
- A pigeon would eat $k_i$ apples from each node in the subtree of $x_i$.
Please help Thanksone to track how much apples are there after $M$ days.
Input
The first line contains three integers $N$, $M$ and $R$, representing $N$ nodes, $M$ days and the root $R$.
Following are $N-1$ lines, each contains two integers $u_i$, $v_i$, representing an edge between $u_i$ and $v_i$.
The following one line contains $N$ integers, representing the initial amount of apples on each nodes.
Finally, the following $M$ lines, each contains three integers $o_i$, $k_i$, $x_i$.
1. If $o_i = 1$, it means that $k_i$ apples grew on node $x_i$ on the $ith$ day.
2. If $o_i = 2$, it means that a pigeon ate $k_i$ apples from each node in the subtree of $x_i$ on the $ith$ day.
Contraints
$1 \le N, M \le 5*10^5$
$1 \le R \le N$
$o_i = {1, 2}$
$1 \le k_i \le 1*10^9$
$1 \le x_i \le N$
Subtask
1. (Testcases 1-3) $1 \le N, M \le 10^3$
2. (Testcases 4-6) $o_i = 1$
3. (Testcases 7-10) No additional constraints.
Output
Output the numbers of apples on $N$ nodes in a line. (Output a whitespace after every integer, including the last one)
Sample Input Download
Sample Output Download
Tags
Discuss
Description
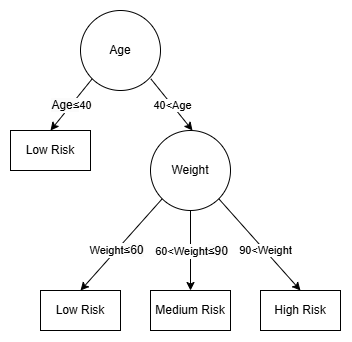
A decision tree is a popular machine learning algorithm that models decisions and their possible consequences. The tree structure consists of nodes representing attributes, branches representing decision rules controlled by threshold values, and leaf nodes representing labels. For each input to a decision tree, we follow the attribute and its corresponding threshold values to decide which subtree to traverse. Once a leaf node is reached, the input is classified to the label on that node.
Here is an example:
For simplicity, we define a decision tree as follows:
Attribute := Non-negative integer
Label := Capital letter
CNT := Positive integer
Threshold := Integer
Thresholds := List of Threshold seperated by `,`
TREE := Attribute '/' CNT '[' Thresholds ']' {CNT+1}*{'(' TREE ')'} | Label
Attribute are numbered from $0$ to $n-1$ if there are $n$ attributes in total. We use a single capital letter to represent a Label and CNT to represent the number of threshold values at a node. It is guaranteed that there are exactly CNT threshold values in Thresholds and CNT+1 subtrees.
Then the previous example can be modeled as:
1/1[40](B)(0/2[60,90](B)(C)(A))
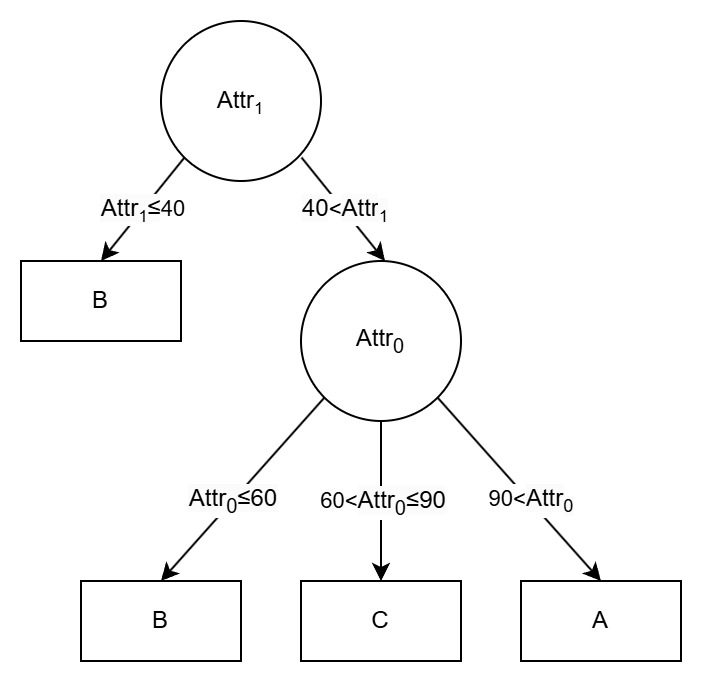
Your task is to classify each input to the decision tree, which is a list of integers where each integer represents the value of an attribute. Here is an example decision tree input if there are three attributes in total, and how to classify this input:
90 45 10
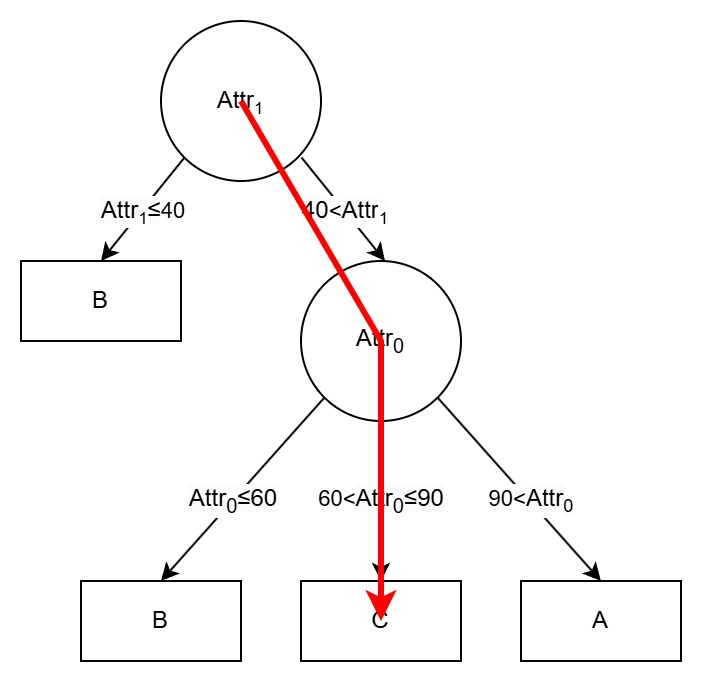
Noted that not every attribute will be used in the decision tree
Input
The first line contains two integers $n$ and $q$, representing the number of attributes and the number of query.
The second line contains a string $S$, representing the decision tree.
The following $q$ lines, each contain $n$ integers, representing the value for each attribute of an input, where $a_{i,j}$ is the $j^{th}$ attribute's value of $i^{th}$ input.
$n \quad q$
$S$
$a_{0,0} \quad a_{0,1} \quad \dots \quad a_{0,n-1}$
$a_{1,0} \quad a_{1,1} \quad \dots \quad a_{1,n-1}$
$\quad\vdots$
$a_{q-1,0} \quad a_{q-1,1} \quad \dots \quad a_{q-1,n-1}$
Constraints
- $1 \leq n \leq 100$
- $1 \leq q \leq 5000$
- $1 \leq |S| \leq 10^6$
- $1 \leq$
CNT$\leq 5$ - $-10000 \leq$
Threshold$\leq 10000$ - $0 \leq$
Attribute$< n$ Labelis a single capital letter.Thresholdvalues in one node are unique and sorted in increaing order
Output
Output $q$ lines, each containing only one capital letter, the classified label of each input to decision tree.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given an array of size $N$, find the inversion count in the array. Two array elements $arr[i]$ and $arr[j]$ form an inversion if $arr[i] > arr[j]$ and $i < j$.
Input
The first line contains an integer $N$, represents the size of the array.
The following one line contains $N$ integers, represent the elements in the array.
Contraints
- $1 \le N, arr[i] \le 5*10^5$
Subtask
- (Testcases 1-5) $1 \le N \le 10^3$
- (Testcases 6-10) No additional constraints.
Output
Output the number of inversions. You should not output a new line ('\n') after your answer.