| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11252 | String Right Shift |
|
| 14510 | Arrange Big orange cat's puzzle III |
|
| 14520 | Pollen Kingdom |
|
Description
Given a string S, you are going to shift part of it.
Specifically, a shift on a string is to move all the characters right but the rightmost characters would be move to the leftmost.
For example, a shift on "abcd" would result in "dabc".
This problem ask you implement a function shift(char *start, char *end) that shift a substring of S starting from start to end.
Input
The first line is a string S. (length of S<=20)
The second is a integer n. (n<=10)
The next n lines, each contains two integers l and r.(l,r<=n)
This means that a shift on S[l]S[l+1]...S[r].
If the length of substring is one(l=r), then you should keep the string unchanged.
All these shift must be done in order.
Output
The result string after all n shift operations.
Sample Input Download
Sample Output Download
Partial Judge Code
11252.cppPartial Judge Header
11252.hTags
Discuss
Description
Last time you helped Orange Cat complete his puzzles. This time, he wants to arrange these puzzles on his shelf.
Each puzzle can be represented by a string composed of digits from 0 to 9. Since the orange cat has a special preference for multiples, he defines a function f(s, x, m) which counts how many substrings of length m in string s representing numbers that are multiples of x.
Now give you n puzzles p1 ~ pn, for each string si, calculate f(si, x1, m), f(si, x2, m), ..., f(si, xk, m) and sort the strings according to the following priority:
- Sort by the value of f(si, x1, m), larger values come first
- If f(si, x1, m) values are equal, compare f(si, x2, m), and so on
- If all values up to f(si, xk, m) are equal, maintain their original relative positions
Divisibility Rules for numbers 2 through 4 (You may also use alternative methods.):
2: The last digit is even.
3: The sum of all digits is divisible by 3.
4: The last two digits form a number divisible by 4.
Input
The first line contains three positive integers n, m, k.
The second line contains k positive integers x1 ~ xk
The following n lines each contain a string si.
Constraints
- 1 <= n <= 1000
- 1 <= | si |, m <= 100
- | s1 | = | s2 | = ... = | sn |
- 1 <= k <= 3
- 2 <= xi <= 4
- All strings contain only 0 ~ 9
Subtasks
- testcases 1 ~ 6: m = | s1 |, k = 1, x1 = 2
- testcases 7 ~ 8: m = | s1 |, k = 2, x1 = 2, x2 = 3
- testcases 9 ~ 10: m = | s1 |, k = 3, x1 = 2, x2 = 3, x3 = 4
- testcases 11 ~ 12: k = 1, x1 = 2
- testcases 13 ~ 14: k = 2, x1 = 2, x2 = 3
- testcases 15 ~ 16: k = 3, x1 = 2, x2 = 3, x3 = 4
Output
Output n lines, where the i-th line contains a string representing the puzzle placed in the i-th position.
Please remember to print "\n" at the end, and dont print space (" ") at the end of every line
Hint1:
Please implement string swapping in bubble sort using strcpy to avoid TLE (Time Limit Exceeded).
Hint2:
The meaning of k in this problem is:
k = 1: You only need to compare the number of multiples of 2
k = 2: You need to first compare multiples of 2, if equal, then compare multiples of 3
k = 3: Following this pattern, compare in priority order of multiples of 2, 3, and 4
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In the previous mission, Bee Agent User333 performed excellently, so he has now been dispatched on a mission to Pollen Kingdom, an ally of Honey Kingdom.
Pollen Kingdom, a nation established by butterflies, also organizes its areas in a regular hexagonal (正六邊形) pattern due to historical reasons. This means the map of Pollen Kingdom consists entirely of hexagonal cells.
To facilitate development, they use a unique coordinate system where each hexagonal cell is represented by coordinate (x,y) as shown below:
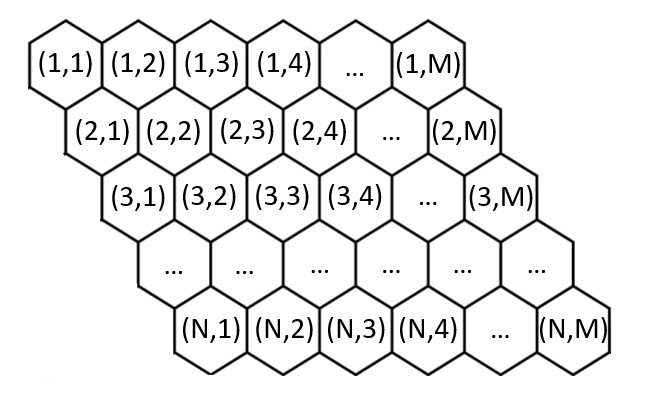
The map is structured such that the first row has coordinates:
(1,1) , (1,2) , ... , (1,M)
The second row then has:
(2,1) , (2,2) , ... , (2,M)
...
In this system, each cell (x,y) is positioned between (x−1,y) and (x−1,y+1).
For any cell located at (x,y), its neighboring cells are:
(x-1,y) , (x-1,y+1) , (x,y-1) , (x,y+1) , (x+1,y-1) , (x+1,y)
Agent User333 has been assigned T missions, each with a different map. On each map, the starting point is always (1,1), and the destination is (N,M).
Each cell on the map contains specific information represented by Ai,j :
- If Ai,j = 'X', the cell is mostly water. For safety reasons, User333 cannot travel across water.
- If Ai,j = '0', the cell is open grassland, which User333 can freely cross.
- If Ai,j is a number between '1' and '5',it indicates the presence of a "magic circle" with a "teleport radius" Ai,j. Standing on this magic circle allows the agent to teleport to any cell within Ai,j steps, ignoring obstacles like water while moving, but they cannot teleport directly onto water cells.
Whenever User333 arrive at a magic circle, you can choose one of the following options:
- Spend one bottle of potion to use the magic circle's teleportation ability.
- Don’t spend any potion and treat it as an open grassland cell.
Agent User333 has been assigned T missions, each with a different map. On each map, the starting point is always (1,1), the destination is (N,M), and he has C bottles of magic potion for that mission.
Input
The first line of input contains a positive integer T, representing the number of maps.
For each map, the input is structured as follows:
- The first line contains three positive integers, N, M, and C, representing that this is an N × M map and that User333 has received C bottles of magic potion for this mission (note: unused bottles cannot be carried over to the next mission; each mission has a separate allocation of potions).
-
The next N lines each contain M entries:
A1,1 , A1,2 , ... , A1,M
A2,1 , A2,2 , ... , A2,M - Each entry Ai,j can be:
- 'X' for water (impassable).
- '0' for open grassland (passable).
- A number between '2' and '5' for a magic circle with that radius.
Constraints
- 1 ≤ T ≤ 10
- 1 ≤ N,M ≤ 500
- 0 ≤ C ≤ 100
- Ai,j ∈ { 'X' , '0' , '2' , '3' , '4' , '5' }
- Each map has at most 100 magic circles.
- The starting point (1,1) and the destination (N,M) are guaranteed to be open grassland.
Subtasks
- Testcases 1~2: N = 1, and there is no magic circle in the map.
- Testcases 3~4: N,M ≤ 10, and there is no magic circle in the map.
- Testcases 5~6: there is no magic circle in the map.
- Testcases 7~8: Ai,j ∈ { 'X' , '0' , '2' , '3' } ; C = 100
- Testcases 9~11: C = 100
- Testcases 12 : C = 1
- Testcases 13 : C = 2
- Testcases 14: No additional restrictions.
Hint:
- For testcases 1 ~ 6: You only need to consider whether you can reach the goal; you don't need to worry about the magic circles.
- For testcases 7 ~ 11: You don't need to worry about the number of potions you have; they are sufficient for you to use all the magic circles.
Output
For each map, output a single line containing "YES" if it is possible to reach the destination from the start point, and "NO" otherwise (without quotes).
Please remember to print "\n" at the end of each line.