| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14482 | Function Composition |
|
| 14487 | Under The Sea |
|
Description
There are three functions:
f(x) = 7x + 1
g(x, y) = 4x + 9y - 2
h(x, y, z) = x - 3y + z - 9
You will be given a expression of these three functions.
For example:
h g f 1 4 1 f 2
which represent:
h(g(f(1), 4), 1, f(2))
= h(g(8, 4), 1, 15)
= h(66, 1, 15)
= 69
Input
A single line with numbers of characters, all the characters are separated with a whitespace.
It is guarantee that the characters contains only f g h and numbers from 0 to 9.
It is guarantee that all the number throughout the entire calculation won't exceed the range of long long.
It is guarantee that the number of characters (excluding whitespace) won't exceed 100.
There won't be any - .
There won't be any adjacent numbers, which means all the numbers are single-digit.
To be clear, the following examples won't appear in the testcase.
h g f 1 4 1 f 23 (two-digit number 23)
h g f -1 4 1 f 2 (negative number -1)
Output
Output the answer of the given expression.
Note that you do NOT need to print '\n' at the end of the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

There is a treasure hidden deep under the sea, and you accidently got a map for the secret treasure.
The map doesn't told you where the treasure were exactly, but it does give you some hint:
We can think of the sea as a 2D structure and divided it into N * M chunks (N rows, M columns).
The (i, j) chunk is assigned to a lucky number Aij, and the treasure is hidden in the luckiest chunk.
The luckiest chunk is defined as following, for an area where the upper left is (Li, Lj) and lower right is (Ri, Rj):
1. If Li == Ri and Lj == Rj, the luckiest chunk is that single chunk.
2. Else, find the middle chunk (Mi, Mj), where Mi = (Li + Ri) / 2 and Mj = (Lj + Rj) / 2, then divide the areas into four small quadrants:
- Upper left is (Li, Lj) and lower right is (Mi, Mj)
- Upper left is (Li, Mj + 1) and lower right is (Mi, Rj)
- Upper left is (Mi + 1, Lj) and lower right is (Ri, Mj)
- Upper left is (Mi + 1, Mj + 1) and lower right is (Ri, Rj)
and calculate the sum of each quadrant. The luckest chunk is in the quadrant with the largest sum.
- If there are more than one quadrant with the same largest sum, then the luckest chunk is at the area with the smallest quadrant number.
- If a quadrant contains no numbers, then the sum of that quadrant is 0.
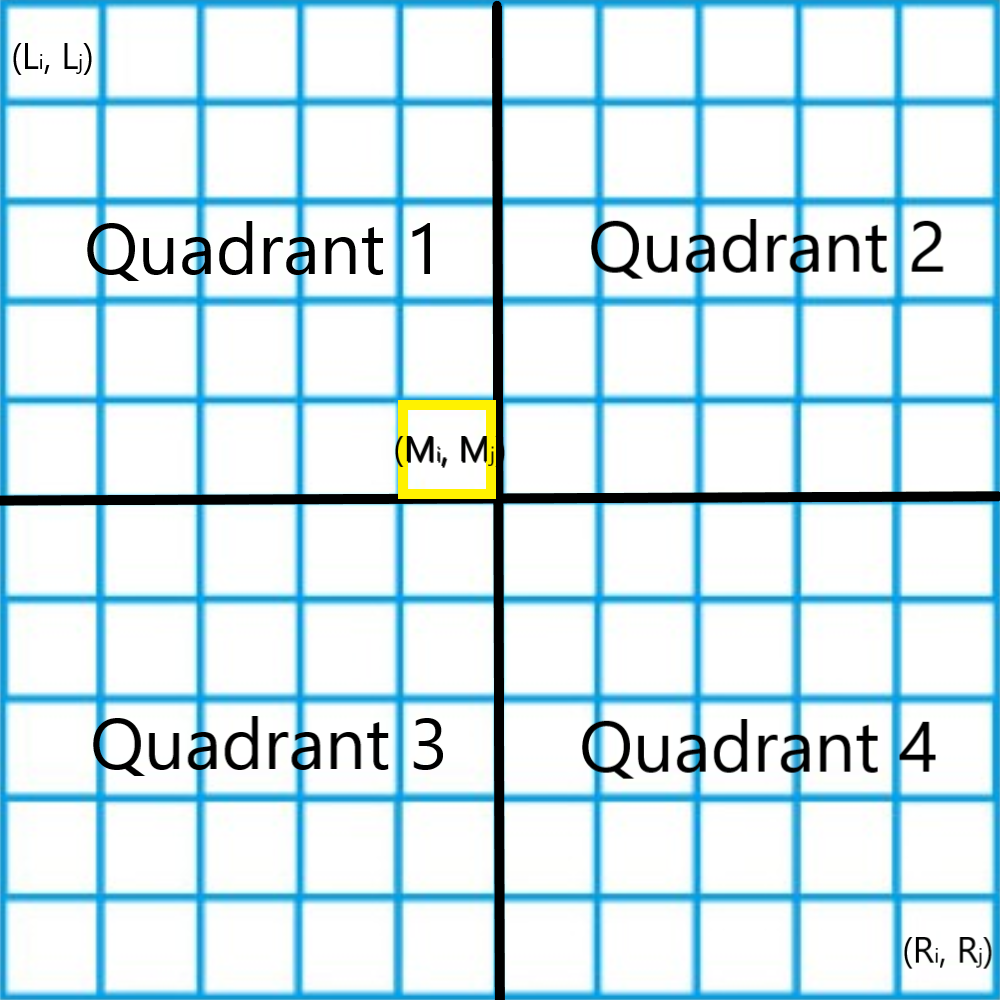
Take the sample input output as an example:
At first, the upper left is (1, 1) and the lower right is (3, 4), so the middle chunk is (2, 2).
Then divide the interval into four quadrants and calculate their sum:
- Upper left is (1, 1) and lower right is (2, 2), sum = 98
- Upper left is (1, 3) and lower right is (2, 4), sum = 59
- Upper left is (3, 1) and lower right is (3, 2), sum = 167
- Upper left is (3, 3) and lower right is (3, 4), sum = 163
Since the quadrant 3 has the largest sum 167, the luckest chunck is in that quadrant and we continue search in that quadrant.
Now, the upper left is (3, 1) and the lower right is (3, 2), so the middle chunk is (3, 1)
Then divide the interval into four quadrants and calculate their sum:
- Upper left is (3, 1) and lower right is (3, 1), sum = 92
- Upper left is (3, 2) and lower right is (3, 2), sum = 75
- Upper left is (4, 1) and lower right is (3, 1), sum = 0
- Upper left is (4, 2) and lower right is (3, 2), sum = 0
Since the quadrant 1 has the largest sum 92, the luckest chunck is in that quadrant and we continue search in that quadrant.
Now, the upper left is (3, 1) and the lower right is (3, 1). Since Li == Ri and Lj == Rj, the luckiest chunk is that single chunk, and the lucky number of that chunk is 92.
Input
The first line contains two integers N and M, represents N rows and M columns.
Next, there would be N lines, each line contains M integers.
For a number Aij, it represents the lucky number of the chunk at the i-th row and the j-th column of the sea.
Constraints:
1 ≤ N ≤ 100
1 ≤ M ≤ 100
0 ≤ Ai ≤ 10000
Output
Output the lucky number of the luckiest chunk.
Note that you do NOT need to print '\n' at the end of the output.