| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12459 | Sierpinski Carpet |
|
| 12991 | Toad Jumping |
|
| 14468 | Big orange cat's puzzle III |
|
Description
This is a Sierpinski Carpet.

The construction of a Sierpinski Carpet is stated as follows. Initially, you are given a white square.
-
Divide the square into nine subsquares in a 3-by-3 grid.
-
Color the center subsquare with black.
-
For the rest eight subsquare, repeat step 1
For example,

Initially (after zero iteration), there is 0 black square in the Sierpinski Carpet.
After one iteration, there is 1 black square in the Sierpinski Carpet.
After two iterations, there are 9 black squares in the Sierpinski Carpet.
After three iterations, there are 73 black squares in the Sierpinski Carpet
Given an integer k, please output number of black squares after k iterations.
Maybe Useless Hint
-
It is suggested to solve this problem using recursion. (Well ... there is mathematic solution, but hope you practice how to design recursion function)
-
Be careful with overflow. Suggest to calculate with long long int.
Input
Input contain a single integer k.
Since there will be overflow issue if k is too big, so in this problem 0 <= k < 10.
Output
Output the number of black squares after the k-th iteration.
Note that there is a newline character after the output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are N stones on the river. The height of the i-th stone is hi for 1 <= i <= N and is colored with color ci. Toad Epep is on the S-th stone (where the leftmost stone is the 1-st stone) and he wants to go the the T-th stone with several jumps.
For each jump from the i-th stone, Epep can jump to the (i-1)-th stone (if it exists), the (i+1)-th stone (if it exists), or any stone colored with the same color ci (if it exists).
Epep will only visit each stone at most once. That is, if Epep jumped to the k-th stone at some time, he won't jumped to the k-th stone again.
The energy cost of jump from i-th to j-th stone is |i-j| x |hi - hj|.
Because Epep ate too much insects and wants to do more exercise, can you help Epep to find the way that cost the most energy (if there are several ways with same maximum energy cost, find the way with maximum jumps) ?
Explanation of Sample IO
All possible moves are listed in the following:
-
2 -> 1 -> 4 -> 3 -> 6 -> 5, which costs 100 energy and 5 jumps
-
2 -> 1-> 4 -> 5, which costs 60 energy and 3 jumps
-
2 -> 3-> 4-> 5, which costs 40 energy and 3 jumps
-
2 -> 3 -> 6 -> 5, which costs 40 energy and 3 jumps
-
2 -> 5, which costs 0 energy and 1 jump
Hint:
1. In this problem, you may need to use an array int jumped[N+1] to record whether a stone i has been visited in the currently expanded path.
2. However, you need to manipulate the int jumped[N+1] array properly as follows:
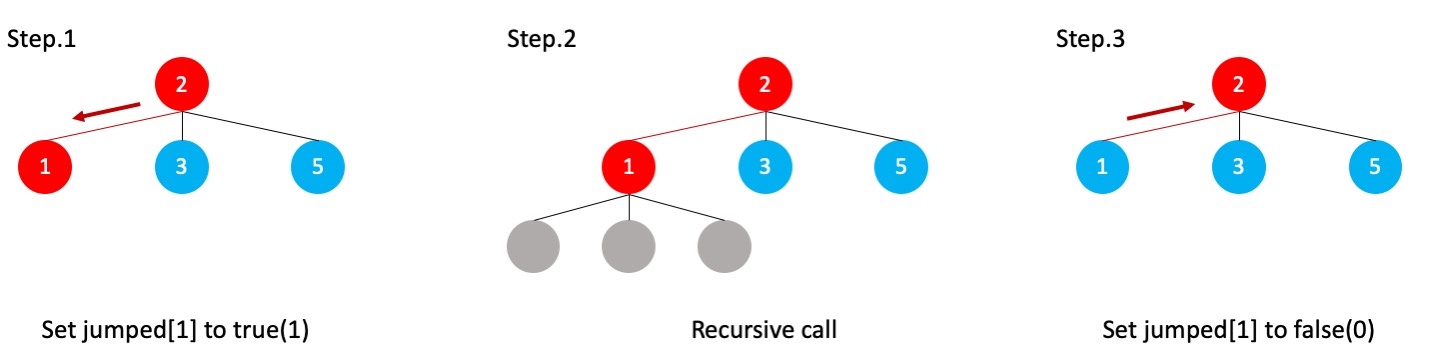
Input
Integers N, S, T are on the first line.
h1, ..., hN are on the second line.
c1, ..., cN are on the third line.
-
1 <= N <= 15
-
1 <= S, T <= N and S != T
-
1 <= hi <= 100000
-
1 <= ci <= 15
Test case description
-
Test case 1: all stones have different colors
-
Test case 2: all stones have the same color
-
The remaining test cases: no additional restrictions
Output
Output two integers E and J, where E is the maximum energy cost and J is the number of jumps in one line. Remember to add \n in the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Based on his previous three experiences (hw4, lab4, mid1), Big Orange Cat has finally figured out which puzzle pieces to choose!
He has now completed 90% of the puzzle. The current puzzle can be represented as an n x m matrix A, with -1 indicating unfilled spaces.
Fortunately, he knows that the sum of numbers in each row should be approximately Si. However, there might be some error, so the actual sum could be in the range [Si - P, Si + P].
He now has k puzzle pieces B1 to Bk. Please tell him how many ways he can use pieces from B to fill the puzzle so that each row's sum falls within the specified range. Also, find the method with the smallest lexicographical order.
The lexicographical order for this puzzle starts from the top-left corner A1,1, then A1,2, and so on. After comparing the first row, move to the second row, following a left-to-right, top-to-bottom rule. For detailed examples, please refer to the sample output.
Input
The first line of input contains four integers n, m, k, P, separated by spaces.
The second line contains k integers B1 to Bk, separated by spaces.
The next n lines each contain m integers Ai,1 to Ai,m.
The last line contains n integers representing S1 to Sn.
Constraints
- 1 <= n, m, k <= 10
- In matrix A, the number of occurrences of -1 will not exceed 10 times, and -1 will appear at most once in each row.
- -1 <= Ai, j <= 10
- 1 <= Bi, Si, P <= 109
Subtasks
- testcases 1 ~ 3: n = 1
- testcases 4 ~ 6: No additional restrictions.
Output
There are two types of output based on different situations:
- If there is no way to fill in the puzzle: Output a single line with
"baganono"(without quotes). - If there is a way to fill in the puzzle:
The first line outputs a positive integer representing the number of possible methods.
The next n lines each output m integers representing the matrix filled using the method with the smallest lexicographical order.
Please remember to print "\n" at the end, and dont print space (" ") at the end of every line.