| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11200 | Tower of Hanoi |
|
| 13690 | Bad Fibonacci's soup |
|
| 14463 | Take 6! |
|
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the moves of the disks. Print the number of disk which is moved in each step.
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
You should print out:
1
2
1
3
1
2
1
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the number of disk which is moved in each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description

Fibonacci's soup is one of the most well-known recipe in Fibonacci's hometown. Besides making soup, Fibonacci also enjoys seeking weird sequences.
We all know that we would not like to add two days before yesterday's soup into Fibonacci's soup, otherwise, It would cause food safety issues, and it would become "Bad Fibonacci's soup", aka "BFS".
One day, Fibonacci found a new sequence again. Since Fibonacci just eat Bad Fibonacci's soup for his lunch and was vomiting, he decided to name this newly found sequence "Bad Fibonacci's sequence".
The following is the formula for the sequence:
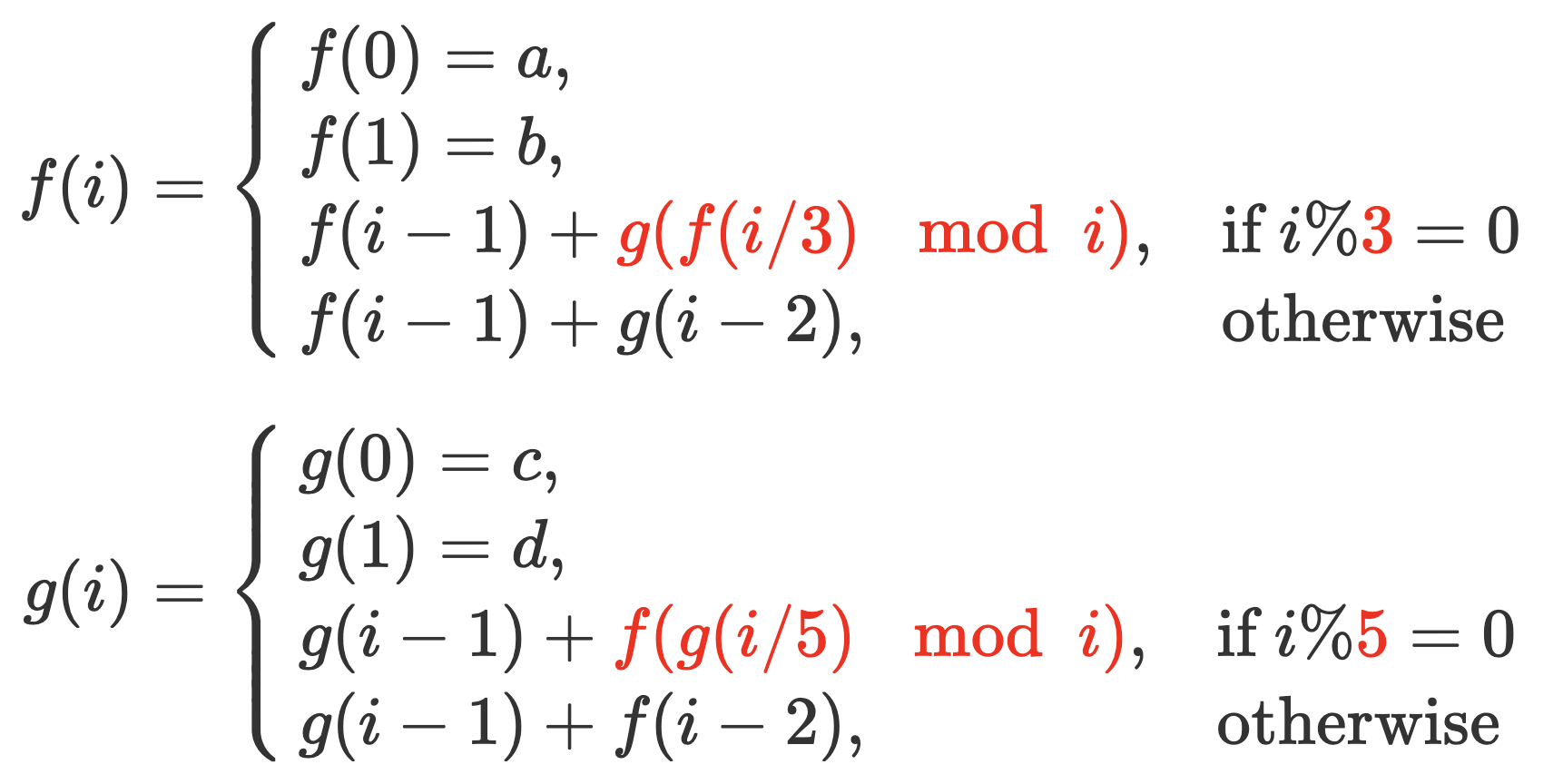
Hint:
If your program gets a "Time Limit Exceeded", your program may solve a same problem (e.g., f(m) or g(n)) too many times. We suggest that you use the dynamic programming method as follows:
- Use a global array to store the solutions to the problems that have been solved so far.
- Then, whenever we attempt to solve a problem, we first check the array to see if the problem is already solved.
- If a solution has been recorded, we can use it directly (that is, no further recursive calls).
- Otherwise, we solve the problem and record its solution in the array.
In this way, we can avoid repeated computation and reduce the computation time significantly.
Input
The input contains one line: nonnegative integers a, b, c, d and n.
Testcase constraints
- For all the testcases: a, b, c, d ≤ 100
- Testcase 1~3: n ≤ 40
- Testcase 4~7: n ≤ 60
- Testcase 8~10: n ≤ 80
Output
Output one line, including f(n) and g(n).
Please remember to print '\n' at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
"Take 6" (also known as "6 Nimmt!") is a card game consisting of 104 cards, each with a number (ranging from 1 to 104) and a certain number of cattle head symbols. The number of cattle headson a card varies, with higher-numbered cards typically carrying more cattle heads. Players aim to finish the game with the fewest cattle heads, as each cattle head counts as a penalty point. The game is played in rounds.
Each card in the game has a certain number of "cattle heads" (penalty points). The distribution of cattle heads across the cards is as follows:
- 1 card with 7 cattle heads—number 55
- 8 cards with 5 cattle heads—multiples of 11 (except 55): 11, 22, 33, 44, 66, 77, 88, 99
- 10 cards with 3 cattle heads—multiples of ten: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
- 9 cards with 2 cattle heads—multiples of five that are not multiples of ten (except 55): 5, 15, 25, 35, 45, 65, 75, 85, 95
- 76 cards with 1 cattle head—the rest of the cards from 1 through 104
Game Rules
- Each player is dealt M cards, and the game consists of M rounds.
- The game starts with P rows of cards, each row beginning with a single starting card.
- During each round:
- All players simultaneously choose a card from their hand to play.
- Once revealed, the cards are arranged in ascending order based on their values, starting with the smallest number.
- Each card must be placed in a row where it is higher than the last card in that row but closest in value.
- If a row already contains five cards, the player placing the sixth card must take all five cards in that row as a penalty. Their card then becomes the new first card in that row.
- If a player's card is smaller than the last card in any row, the player must take all the cards from the row with the highest last card (as a penalty) and place their card as the new first card of that row.
- The game continues until all players have played all their cards.
The goal is to avoid collecting cattle heads, as they represent penalty points. The player with the fewest cattle heads at the end of the game wins.
Input
The input starts with a line containing three integers N , M , and P , which denote the number of players, the number of cards each player holds, and the number of rows on the table.
The next P lines each contain one integer Di , representing the starting card in row i on the table.
The following N lines each contain M integers Ci,1 ,Ci,2 ,...,Ci,M , where Ci,j represents the card that player i plays in round j. Each player will play one card per round.
Constraints
- 2 ≤ N ≤ 10
- 1 ≤ M ≤ 50
- 1 ≤ N×M ≤ 100
- 1 ≤ P ≤ 4
- 1 ≤ Di , Ci,j ≤ N×M + P
- for all triple (i, j, k) , Di ≠ Cj,k
Subtasks
- Testcases 1~2: P = 1
- Testcases 3~4: M = 1
- Testcases 5~6: N = 2
- Testcases 7~10: No additional restrictions.
Output
The output should consist of N lines, where each line i contains a single integer representing the total number of cattle head for player i at the end of the game. Each player's cattle head count reflects the penalties incurred throughout the game.
Sample explanation
At the beginning, there are two rows of cards on the table, with 11 and 6 cards respectively.

In the first round, the four players each play a card: 12, 1, 7, and 8.

Player 2 (green) plays card 1 first. Since there are no cards on the table smaller than 1, this player must take all the cards from the row with the highest last card.The player takes the card numbered 11 and earns 5 cattle heads.
Next, the cards are placed in order: 7 is placed after 6, 8 is placed after 7, and 12 is placed after 8.

In the second round, the four players each play a card: 5, 13, 2, and 14.

Player 3 (purple) plays card 2 first, and the cards are placed in order: 2 is placed after 1, 5 is placed after 2, 13 is placed after 12, and 14 is placed after 13.
Since Player 4 (gray)’s card (14) is the sixth card in the row, as a penalty, they must take the previous five cards in the row and earn 5 cattle heads.

The two new rows will become the ones shown in the image below.

In the third round, the four players each play a card: 9, 10, 4, and 3.
Player 4 (gray) plays card 3 first, but since there are no cards on the table smaller than 3, this player must take all the cards from the row with the highest last card.

The player takes the card numbered 14 and earns 1 cattle head.
Next, the cards are placed in order: 4 is placed after 3, 9 is placed after 5, and 10 is placed after 9.
