| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12486 | Tower of Hanoi |
|
| 14040 | GCD |
|
| 14437 | Bins and balls |
|
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the optimal moves of the disks. Print the number of disk which is moved in each step.
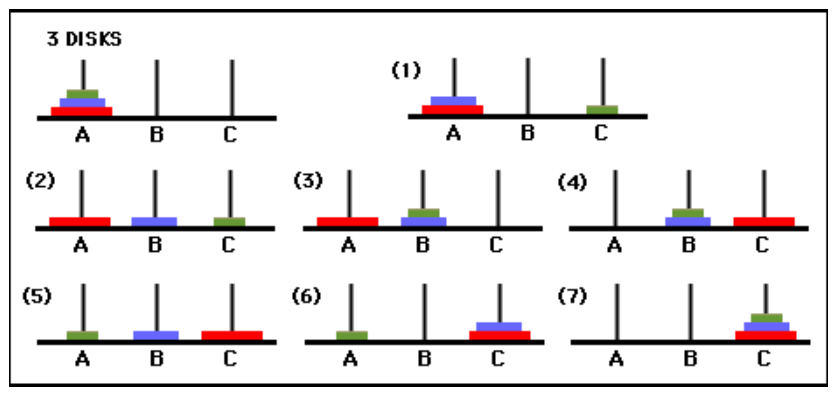
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the information of each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Calculate the greatest common divisor of two integers.
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted 
For example, the GCD of 8 and 12 is 4, that is,
Input
Two integers x, y
1 < x, y< 10000
Output
Output the greatest common divisor.
Don't forget to include '\n'
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are n distinct balls and k identical bins. Write a program to determine how many ways are there to throw the balls into the bins, such that no bin are emtpy.
Take n = 5, k = 3 for example, there are 25 ways in total. One of the way is: [1, 2], [3, 5], [4], where each [ ] denote a bin. Also note that [3, 5], [4], [1, 2] is considered the same way, since the bins are identical.
Input
The first line contains two integer n, k, seperated by a blank.
Constrain
- 1 <= k <= n <= 15.
Output
Output a integer in one line: the number of ways. You need to add '\n' in the end of output.
Hint
Let f(n, k) be the number of ways when there are n balls and k bins. Then we can consider two ways to put the n-th ball:
- Put it into a bin that have no other ball, then the number of ways to put other balls is f(n - 1, k - 1)
- Put it into a bin that have already have other balls (which have k choices of bin), the number of ways ot put other balls is f(n - 1, k)
Hence we have the recurrence f(n, k) = f(n - 1, k - 1) + k * f(n - 1, k), and f(n, k) = 1 when n = k.
You may reference Stirling number of second kind for more details.
