| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14348 | 2024_DS_Summer_Exam1_pA |
|
| 14349 | 2024_DS_Summer_Exam1_pB |
|
| 14350 | 2024_DS_Summer_Exam1_pC |
|
| 14351 | 2024_DS_Summer_Exam1_pD |
|
Description
Charlotte can now write many Arabic numerals, so her teacher gave her an advanced assignment.
First, given an array A of N numbers and Q queries.
Each query consists of two numbers L and R. For each query, Charlotte needs to answer how many i satisfy L ≤ A[i] ≤ R in the given array A (where i is integer and 1 ≤ i ≤ N).
Please help Charlotte complete her homework.
Input
The first line contains two numbers N, Q (1 ≤ N ≤ 2 × 105, 1 ≤ Q ≤ 2 × 105).
The second line contains N numbers representing A[1], A[2], ..., A[N] (1 ≤ A[i] ≤ 108).
The next Q lines each contain two numbers L and R (guaranteed that 1 ≤ L ≤ R ≤ 108).
Output
Output Q lines, each representing the answer to the corresponding query.
Please add a newline('\n') at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
You are given a sequence of length N. You can repeatedly choose any two numbers from the sequence and add them together, placing the sum back into the sequence, until only one number remains (thus, you will perform a total of N−1 additions).
Each addition has a cost, which is the sum of the two numbers chosen. For example, the cost of adding 1 and 10 is 11.
Your task is to add the N numbers together in such a way that the total cost is minimized.
Input
Each test case starts with a positive integer N (2 ≤ N ≤ 200000), followed by N positive integers (each less than 100000).
Output
print the minimum total cost of addition on a single line.
Remember to print a ‘\n’ at the end of the output.
HINT
To achieve the minimum total cost, always combine the two smallest available numbers first.
Note: The total cost may exceed 231 - 1
Sample Testcase 1:
Initial: The initial sequence is {1, 2, 3}.
Step 1: We choose the numbers 1 and 2. After adding them, the sequence becomes {3, 3}, and the cost is 1+2=3.
Step 2: We choose the numbers 3 and 3. After adding them, the sequence becomes {6}, and the cost is 3+3=6.
Final: The total cost is 3+6=9.
Sample Testcase 2:
Initial: The initial sequence is {1, 2, 3, 4}.
Step 1: We choose the numbers 1 and 2. After adding them, the sequence becomes {3, 3, 4}, and the cost is 1+2=3.
Step 2: We choose the numbers 3 and 3. After adding them, the sequence becomes {4, 6}, and the cost is 3+3=6.
Step 3: We choose the numbers 4 and 6. After adding them, the sequence becomes {10}, and the cost is 4+6=10.
Final: The total cost is 3+6+10=19.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given n rectangle Ri, i = 1, 2, ..., n in the Euclidean plane. The lower left point and upper right point of Ri is (0, 0) and (ui, ri) repectively.
Find the number of pairs (i, j) such that Ri can be contained in Rj after rotating 90o or 0o. Formally speaking, find the number of pairs (i, j) that satisfy at least one of the following conditions:
- ui ≤ uj and ri ≤ rj
- ui ≤ rj and ri ≤ uj
For example, the following two rectangles satisfy the condition, since the blue rectangle can be contained in the red rectangle by rotating 90o (see picture on right hand side).
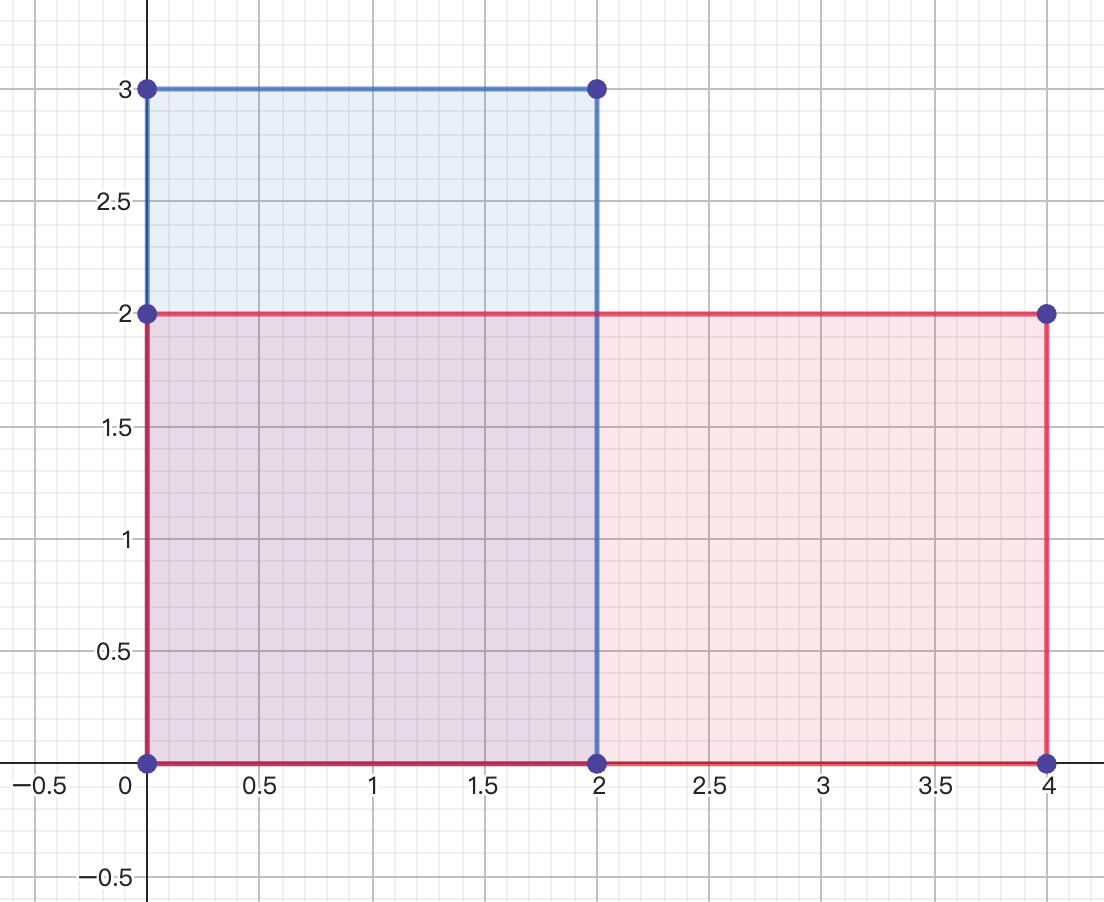
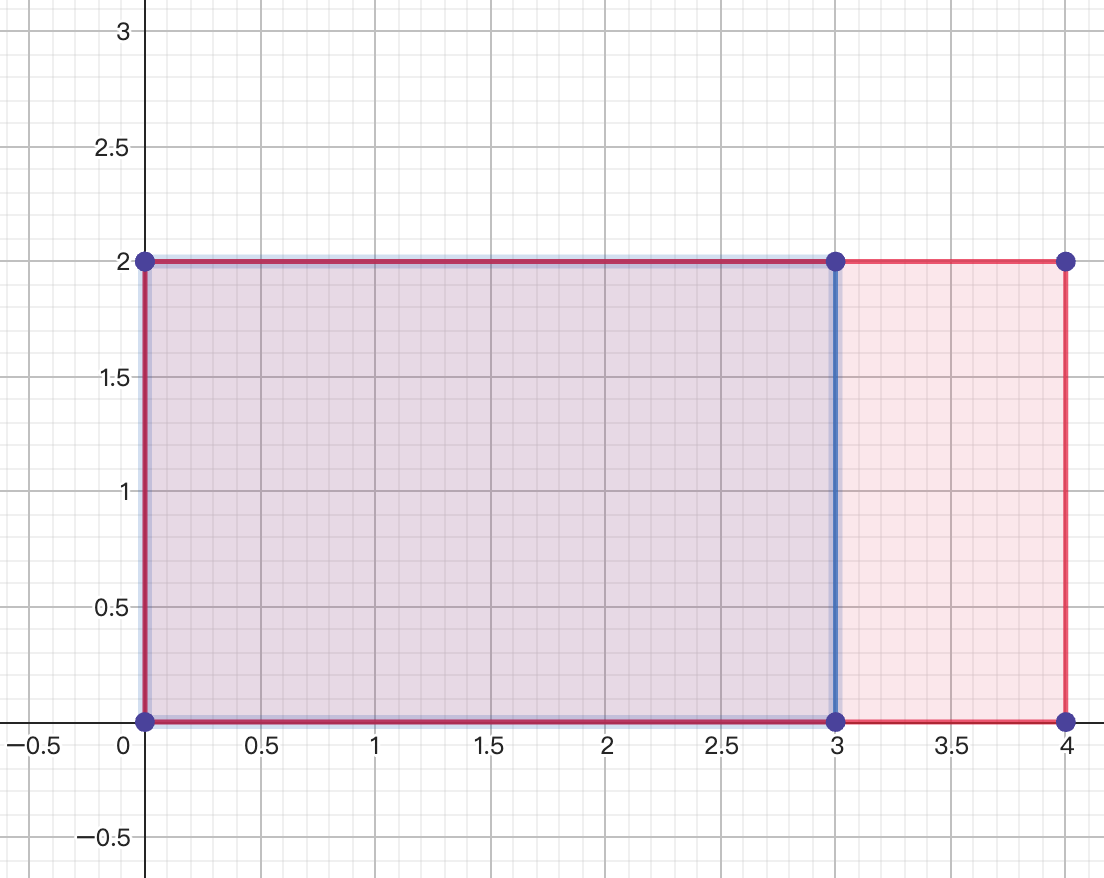
Input
The first line contains an integer n. For the next n line, each line contains two integers ui, ri, i = 1, 2, ..., n.
Constrain
- 1 ≤ n ≤ 105
- 1 ≤ ui, ri ≤ 109, i = 1, 2, ..., n
- No two rectangles are identical after rotating 90o or 0o.
Output
Output one integer: the number of pairs satisfying the condition above.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are n gas stations on a highway, the i-th station is located at the xi km of the highway, and you can get vi unit of fuel (an unit of fuel can drive 1 km) if you stop and refuel at this station. Also, you can't stop at the i+1, i+2, ..., n-th station if you don't stop at the i-th station.
Now you are at the 0 km of the highway and your car has V unit of fuel. Besides, there are q places you want to visit, the i-th place is located at the pi km of the highway. Now, for each place, answer at least how many gas station you need to stop in order to reach the place.
Hint
Let Ti be the total unit of fuel you will have if you stop at 1, 2, ... i-th station. Then Ti = V + v1 + v2 + ... + vi by definition, which can be computed in O(n) time using the following recurrence:
- T0 = V (We define T0 as the total unit of fuel if you don't stop at any station)
- Ti = Ti-1 + vi, i = 1, 2, ..., n
Input
The first line contains two integers: n, q, V.
For the next n lines, each line contains two integers: xi, vi (i = 1, 2, ..., n).
The last line contains q integers: p1, p2, ..., pn.
Constrain
- 1 ≤ n, q ≤ 105
- 1 ≤ x1 < x2 < ... < xn ≤ 109
- 1 ≤ vi ≤ 109, i = 1, 2, ..., n
- 1 ≤ pi ≤ 109, i = 1, 2, ..., q
Output
Output n lines, each line contains one integer: the answer of the i-th place. If it is impossible to reach the place, output -1.