| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13928 | Largest Rectangle |
|
| 13930 | I'm reference |
|
| 14215 | Emergency Evacuation |
|
| 14336 | Divisor Jumps |
|
| 14344 | I2P(II)2024_Kuo_Final_rule |
|
Description
There are N bars line up in a row. The height of the i-th bar is hi, and the width of each bar is 1. Please find the largest rectangle in it.
Sample test:
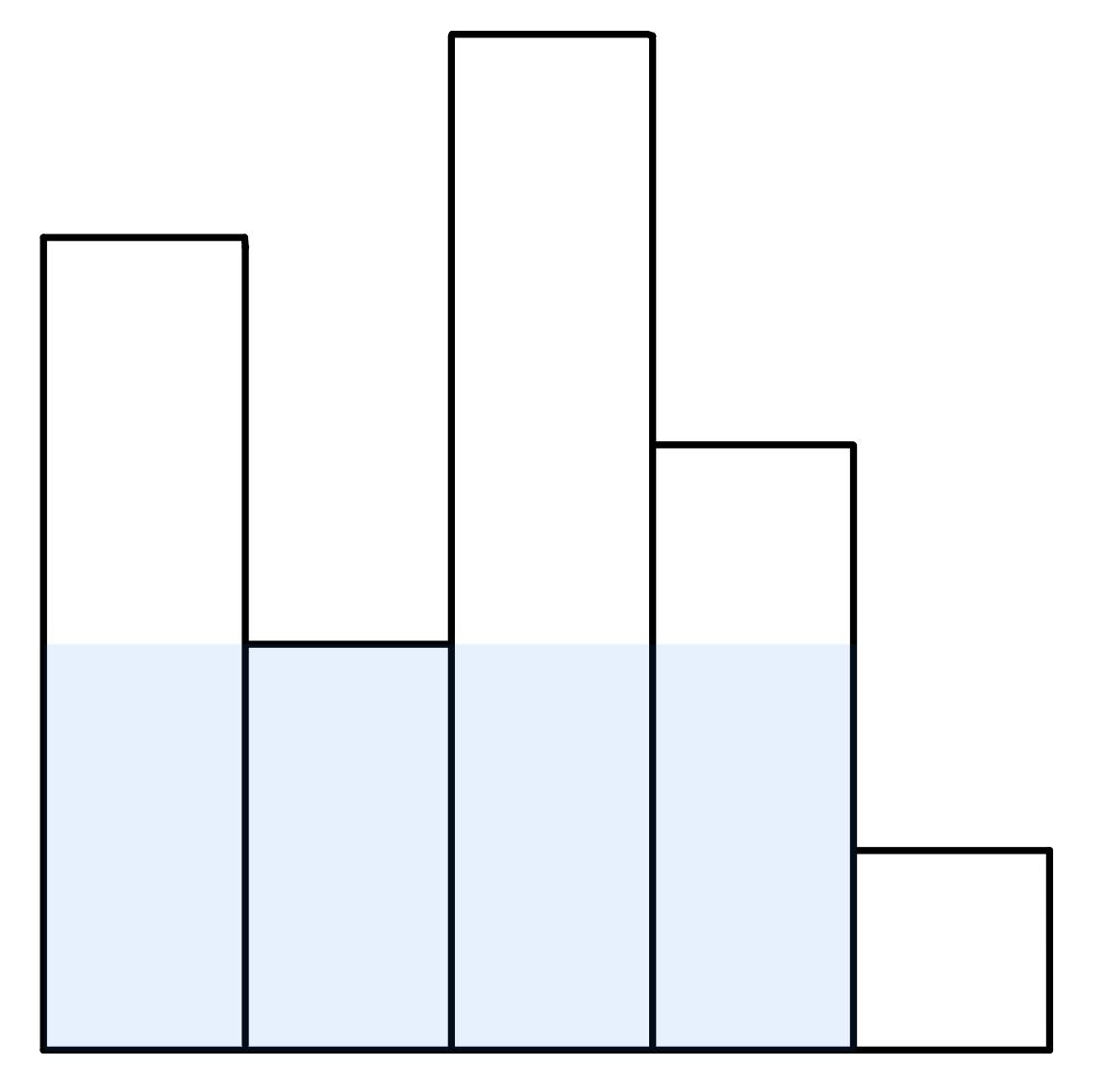
Input
The first line has an integer T, means there are T testcases.
The first line of each testcase contains an integer N, and the second line contains N integers h1 ~ hN.
1 <= hi <= 1e9.
1 <= T <= 10.
In testcase 1 ~ 4: 1 <= N <= 1000.
In testcase 5 ~ 8: 1 <= N <= 2e5.
Output
Please print the area of the largest rectangle for each testcase.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
下載後將副檔名改成zip(.cpp和.h為相同檔案,下載一個即可)
更改副檔名教學 :
打開任意資料夾 >> 點擊上方 "檢視" >> 勾選 "副檔名" >> 將.cpp或.h更改成.zip
解壓縮 >> 點進 reference 目錄 >> 點進 en 目錄 >> Main_Page.html 就可以看到完整的cpprefernce.com離線版
===================================================================================================
Download the partial judge code and change the extension to .zip. (.cpp and .h is the same file. Donwload one of them is enough.)
Open the folder with the file in it >> click "view" >> check "File name extensions" >> change .cpp or .h to .zip
Unzip the file >> click "reference" > click "en" >> open "Main_Page.html". Then you can use the offline version of cppreference.com.
Input
Output
Sample Input Download
Sample Output Download
Partial Judge Code
13930.cppPartial Judge Header
13930.hTags
Discuss
Description
The Japanese government plans to increase the number of inbound tourists to forty million in the year 2020, and sixty million in 2030. Not only increasing touristic appeal but also developing tourism infrastructure further is indispensable to accomplish such numbers.
One possible enhancement on transport is providing cars extremely long and/or wide, carrying many passengers at a time. Too large a car, however, may require too long to evacuate all passengers in an emergency. You are requested to help estimating the time required.
The car is assumed to have the following seat arrangement.
- A center aisle goes straight through the car, directly connecting to the emergency exit door at the rear center of the car.
- The rows of the same number of passenger seats are on both sides of the aisle.
A rough estimation requested is based on a simple step-wise model. All passengers are initially on a distinct seat, and they can make one of the following moves in each step.
- Passengers on a seat can move to an adjacent seat toward the aisle. Passengers on a seat adjacent to the aisle can move sideways directly to the aisle.
- Passengers on the aisle can move backward by one row of seats. If the passenger is in front of the emergency exit, that is, by the rear-most seat rows, he/she can get off the car.
The seat or the aisle position to move to must be empty; either no other passenger is there before the step, or the passenger there empties the seat by moving to another position in the same step. When two or more passengers satisfy the condition for the same position, only one of them can move, keeping the others wait in their original positions.
The leftmost figure of Figure C.1 depicts the seat arrangement of a small car given in Sample Input 1. The car have five rows of seats, two seats each on both sides of the aisle, totaling twenty. The initial positions of seven passengers on board are also shown.
The two other figures of Figure C.1 show possible positions of passengers after the first and the second steps. Passenger movements are indicated by fat arrows. Note that, two of the passengers in the front seat had to wait for a vacancy in the first step, and one in the second row had to wait in the next step.
Your task is to write a program that gives the smallest possible number of steps for all the passengers to get off the car, given the seat arrangement and passengers’ initial positions.
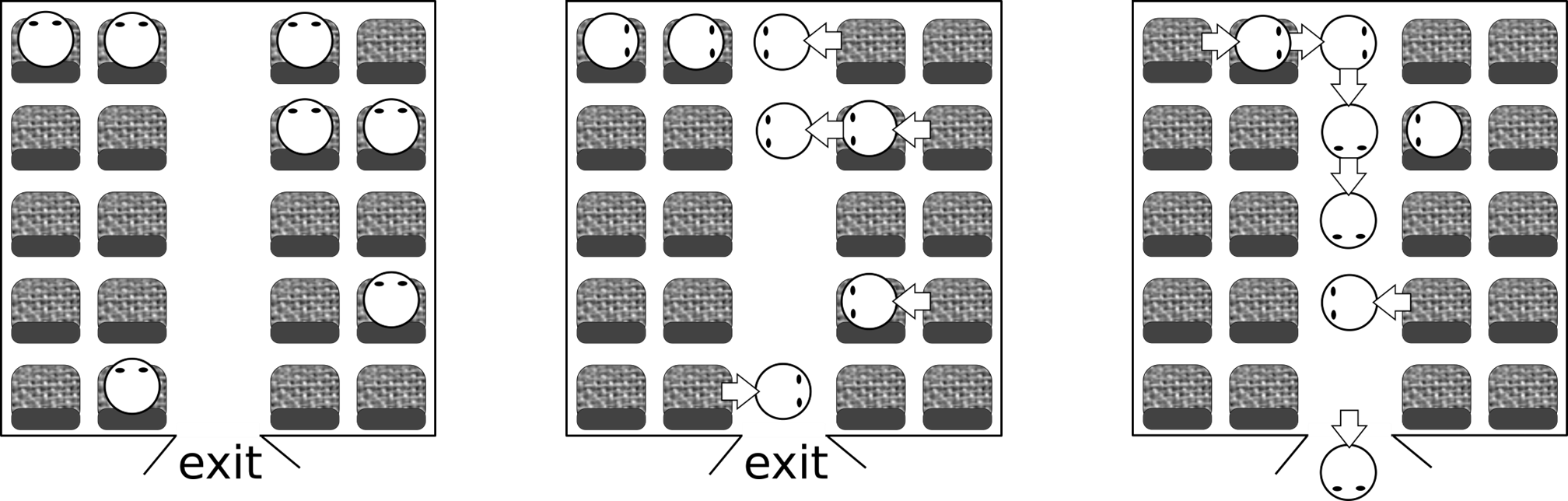
Figure C.1. Simple Model
Input
The input consists of a single test case of the following format.
$r \quad s \quad p$
$i_1 \quad j_1$
$\vdots$
$i_p \quad j_p$
Here, $r$ is the number of passenger seat rows, $s$ is the number of seats on each side of the aisle, and $p$ is the number of passengers. They are integers satisfying $1 \le r \le 500$, $1 \le s \le 500$, and $1 \le p \le 2rs$.
The following $p$ lines give initial seat positions of the passengers. The $k$-th line with $i_k$ and $j_k$ means that the $k$-th passenger’s seat is in the $i_k$-th seat row and it is the $j_k$-th seat on that row. Here, rows and seats are counted from front to rear and left to right, both starting from one. They satisfy $1 \le i_k \le r$ and $1 \le j_k \le 2s$. Passengers are on distinct seats, that is, $i_k \ne i_l$ or $j_k \ne j_l$ holds if $k \ne l$.
Output
The output should be one line containing a single integer, the minimum number of steps required for all the passengers to get off the car.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are \(N\) stones, numbered \(1,2,...,N\).
There is a frog who is initially on Stone \(x\). He will repeat the following action some number of times to reach Stone \(N\):
- If the frog is currently on Stone \(i\), jump to Stone \(i + d\) or Stone \(i - d\) where \(d\) is a divisor of \(i\).
Here, an integer \(b\) is said to be a divisor of \(a\) if there exist an integer \(c\) such that \(a = b \times c\).
For each starting stone \(1 \leq x \leq N\), find the minimum number of jumps to reach Stone \(N\).
Input
The only line contains an integer \(N\).
\(N\)
Constraints
- \(1 \le N\le 10^6\)
Output
Please output \(N\) integers in a line, each followed by a space.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
-
Only C and C++ are allowed. Solving problems with other languages (e.g. python, java) are forbidden, otherwise you'll get zero point.
-
No restrictions on standard library usage.
-
-
Paper references, electronic devices, or other items that may contain any information relative to this exam are not allowed.
-
Before leaving, please tell TAs, we'll check if your accepted / partially accepted submissions are all written in C or C++. After you pass the check, you may return the account strip and leave.
-
The score of the exam will be total number of testcases you passed / number of testcases.
-
Recommended problem-solving order: 13928 -> 14215 -> 14336