| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 14328 | Panda's Bus Service: Operation BambooPath |
|
Description

A bus company is planning to optimize its city routes, and they've enlisted Panda's help to ensure the city is well-connected. The city is represented as a weighted directed graph, where each bus stop is a node, and the routes between them are edges with different travel times. The company wants to ensure that the main terminal(s), Terminal A and/or Terminal B, have optimal routes to the downtown hub, City Center. As the route planner, your job is to find the shortest subgraph that can guarantee efficient routes from the specified terminal(s) to the City Center.
Example Question:
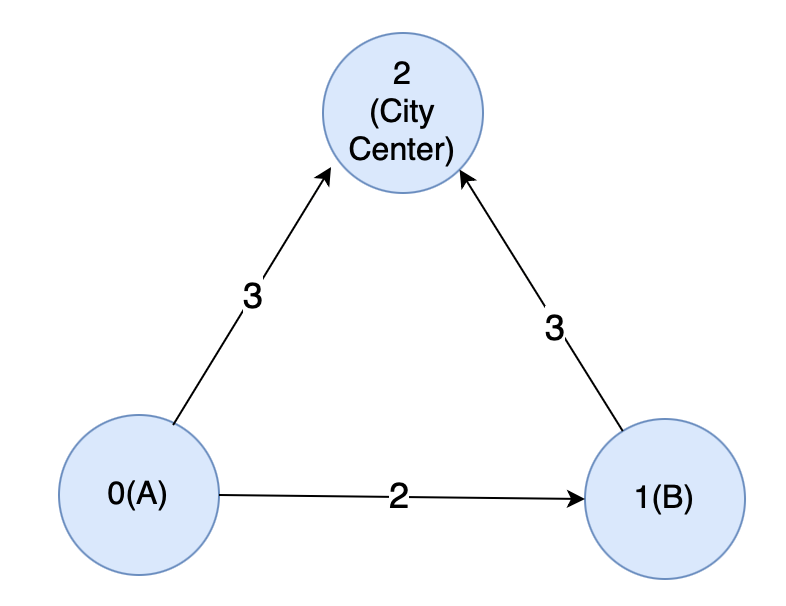
Given the Input:
n = 3
m = 3
edges -> 0, 1, 2 | 0, 2, 3 | 1, 2, 3
t = 2
A = 0, B = 1, City Center = 2.
Output: 5
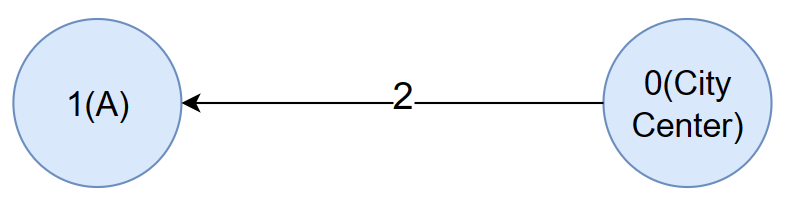
Given the Input:
n = 2
m = 1
edges -> 0, 1, 2
t = 1
A = 1, City Center = 0
Output: -1
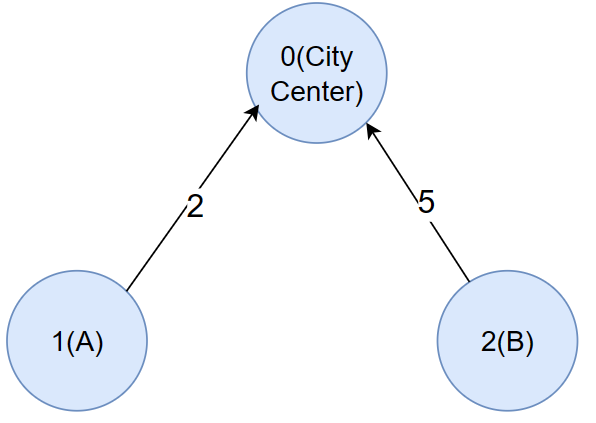
Given the Input:
n = 3
m = 2
edges -> 1, 0, 2 | 2, 0, 5
t = 2
A = 1, B = 2, City Center = 0
Output: 7
Hint
Start by handling the condition where there's only one terminal.
Input
You are given an integer n, representing the number of bus stops in the city. The stops are numbered from 0 to n - 1.
You are given an integer m, representing how many edges will be provided, followed by m lines where each line consists of three numbers ‘fromi toi wi’ representing a bus route from stop fromi to stop toi with a travel time of wi.
You are also given an additional integer t, which specifies how many terminals should have routes to the City Center (1 <= t <= 2):
• If t = 1, only Terminal A (A) will be considered, and the input will only contain A and dest.
• If t = 2, both Terminal A (A) and Terminal B (B) must have optimal routes to the City Center city (dest). Additionally, you are given up to three distinct integers A, B, and dest, representing the stops for Terminal A (A), Terminal B (B), and City Center (dest), respectively.
Constraints:
2 <= n <= 100000
0 <= m <= 100000
0 <= from, to, A, B, City Center <= n – 1
from != to / A != B != City Center
1 <= w <= 100000
Output
Your task is to determine the minimum travel time of a subgraph that allows passengers to travel from the specified terminal(s) to the City Center (dest):
1. If t = 1, find the shortest subgraph from Terminal A (A) to the City Center.
2. If t = 2, find the shortest subgraph that allows passengers to travel from both Terminal A (A) and Terminal B (B) to the City Center (dest). If it's impossible to reach the City Center from the specified terminal(s), return -1.
Remember end of line.